1.Общие сведения о топографических материалах
Топографические материалы, являющиеся уменьшенным спроецированным изображением участков земной поверхности на плоскость, подразделяют на карты и планы.
Топографическим планом называют уменьшенное и подобное изображение на бумаге ситуации и рельефа местности. Подобное изображение получают при ортогональном проецировании участков земной поверхности размером, не превышающим 20 х 20 км, на горизонтальную плоскость. В уменьшенном виде такое изображение представляет план местности. Ситуацией называют совокупность предметов местности, рельефом — совокупность различных форм неровностей земной поверхности. План местности, составленный без изображения рельефа, называют ситуационным (контурным).
Таким образом, план — это чертеж, состоящий из горизонтальных положений-отрезков, полученных ортогональным проектированием соответствующих отрезков местности (строительных сооружений, дорог, элементов гидрографии и т. д.).
В виде плана составляют ряд строительных чертежей, входящих в проектно-техническую документацию, необходимую при возведении зданий и сооружений. Такие чертежи позволяют как бы рассматривать сверху уменьшенные изображения строительных конструкций.
Изображение больших по размерам участков земной поверхности на плоскости нельзя получить без искажений, т. е. с сохранением полного подобия. Такие участки ортогонально проецируют на поверхность эллипсоида, а затем с поверхности эллипсоида по определенным математическим законам, называемым картографическими проекциями (проекция Гаусса-Крюгера) переносят на плоскость. Полученное таким образом уменьшенное изображение на плоскости называют картой.
Топографической картой называется уменьшенное, обобщенное и построенное по определенным математическим законам изображение значительных участков поверхности Земли.
Зрительное восприятие образа земной поверхности, ее характерных черт и особенностей связано с наглядностью планов и карт. Наглядность обусловливается выделением типичных черт местности, определяющих ее отличительные особенности, путем обобщений — генерализации, а также применением для изображения земной поверхности топографических условных знаков — системы условных обозначений.
Карты и планы должны быть достоверными, т. е. сведения, составляющие их содержание на определенную дату, должны быть правильными, отвечающими состоянию изображенных на них объектов. Важным элементом достоверности является полнота содержания, включающая необходимый объем сведений и их разносторонность.
ДИПЛОМНЫЙ ПРОЕКТ/РАБОТА Тема работы Технология ремонта линейной ...
... МАГИСТРАЛЬНЫЙ ГАЗОПРОВОД, УЧАСТОК ТРУБОПРОВОДА, ИЗОЛЯЦИЯ, АДГЕЗИЯ, КОНТРОЛЬ КАЧЕСТВА, АНОДНОЕ ЗАЗЕМЛЕНИЕ, КАТОДНАЯ ЗАЩИТА, ЭЛЕКТРОХИМИЧЕСКАЯ ЗАЩИТА (ЭХЗ). Объектом исследования является изоляционное покрытие на действующем магистральном газопроводе. Цель работы: описать технологию ремонта линейной части магистрального газопровода ...
По назначению топографические карты и планы делятся на основные и специализированные. К основным относятся карты и планы общегосударственного картографирования. Эти материалы многоцелевого назначения, поэтому на них отображают все элементы ситуации и рельефа.
Специализированные карты и планы создают для решения конкретных задач отдельной отрасли. Так, дорожные карты содержат более детальную характеристику дорожной сети. К специализированным относят и изыскательские планы, используемые только в период проектирования и строительства зданий и сооружений. Кроме планов и карт к топографическим материалам относят профили местности, представляющие собой уменьшенное изображение вертикального разреза земной поверхности вдоль выбранного направления. Профили местности являются топографической основой при составлении проектно-технической документации, необходимой при строительстве подземных и наземных трубопроводов, дорог и других коммуникаций.
2.Масштабы
Степень уменьшения изображения на плане контуров местности, иначе отношение длины отрезка линии на плане (карте) к соответствующему горизонтальному положению этого отрезка на местности, называется масштабом. Масштабы делятся на численные и линейные.
Численный масштаб-дробь, числитель которой — единица, а знаменатель — число, показывающее, во сколько раз уменьшены линии и предметы при изображении их на плане (карте).
На каждом листе карты или плана подписывается его численный масштаб в виде: 1:1000; 1:5000; 1:10 000; 1:25000 и т.д.
Линейный масштаб — графическое выражение численного масштаба (рис.9) . Для построения линейного масштаба проводят прямую линию и на ней несколько раз откладывают одно и то же расстояние в сантиметрах, называемое основанием масштаба. Основание обычно берут длиной в два сантиметра. Длину линии на местности, соответствующую основанию линейного масштаба, подписывают слева направо по ходу ее нарастания, а первое левое основание делят еще на 10 частей. Практическая точность линейного масштаба ±0,5мм, что соответствует 0,02-0,03 основания масштаба.
Для более точных графических работ на плане пользуются поперечным масштабом, позволяющим измерять отрезки с точностью 0,01 его основания.
Поперечный масштаб представляет собой график, основанный на пропорциональном делении (рис.10); для построения масштаба на прямой откладывают несколько раз основания масштаба; из точек делений восставляют перпендикуляры; первое левое основание делят на 10
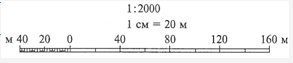
Рис.

Рис.9. Линейный и численный масштабы на топографических картах
частей, а на перпендикулярах откладывают также 10 равных частей и через точки отложения проводят линии, параллельные основанию, как показано на рис. 10. Из подобия треугольников ВDЕ и Bdeследует de/DE = Bd/BD или de= Bd∙DE/BO, но DЕ = АB/10, Bd= BD/10. Подставляя значения DE и Bd, получим de= АB/100,т. е. наименьшее деление поперечного масштаба равно сотой доле основания. По масштабу с основанием 10мм можно определять длины отрезков с точностью 0,1мм. Применение любого масштаба, даже поперечного, не может обеспечить точности выше определенного предела, зависящего от свойств человеческого глаза. Невооруженным глазом с расстояния нормального зрения (25см) можно оценить на плане размер, не превосходящий 0,1мм (детали объектов местности меньше 0,1мм изобразить на плане нельзя).
Структура комплексного бизнес-плана и роль анализа в разработке ...
... а значит, инвестирование в новые сферы бизнеса. Масштабы, сложность и разнообразие ... план организации по маркетингу, план производства, план по труду и финансовый план. ... и др. 1.2 Значение анализа во внутрипроизводственном планировании ... разработками. Кроме того, они обладают высококвалифицированным персоналом и в ... факторы, обуславливающие повышение роли планирования в организациях. Рассмотрим важнейшие ...
Точность масштаба характеризуется горизонтальным расстоянием на местности, соответствующим на плане 0,1мм. Например, для планов, вычерченных в масштабе 1:500, 1:1000, 1:2000, точность масштаба соответственно равна 0,05, 0,1, 0,2м. Точностью масштаба определяется степень обобщения (генерализации) подробностей, которые могут быть изображены на плане (карте) того или иного масштаба.
3.Условные знаки на планах и картах
На топографических картах и планах изображают разные объекты местности: контуры населенных пунктов, сады, огороды, озера, реки, линии дорог, электропередачи. Совокупность этих объектов называется ситуацией. Ситуацию изображают условными знаками.
Условные знаки, обязательные для всех учреждений и организаций, составляющих топографические карты и планы, устанавливаются Федеральной службой геодезии и картографии России (Роскартография) и издаются либо отдельно для каждого масштаба, либо для группы масштабов. Хотя число условных знаков велико (около 400), они легко запоминаются, так как внешне напоминают вид и характер изображаемых объектов.
Условные знаки подразделяют на пять групп: площадные, линейные, внемасштабные, пояснительные, специальные.
Площадные условные знаки (рис.11, а)применяют для заполнения площадей объектов (например: пашни, леса, озера, луга); они состоят из знака границы объекта (точечный пунктир или тонкая сплошная линия) и заполняющих его изображений или условной окраски; например, на условном знаке 1 показан березовый лес; цифры (20/0,18)∙4 характеризуют древостой: числитель — среднюю высоту, знаменатель — среднюю толщину ствола, 4 — среднее расстояние между деревьями.
Линейными условными знаками оказывают объекты линейного характера (дороги, реки, линии связи, электропередачи), длина которых выражена в данном масштабе. На условных изображениях приводятся различные характеристики объектов; например, на шоссе 7 показаны, м: ширина проезжей части — 8, всей дороги — 12; на железной дороге 8, м: +1,8 — высота насыпи, -2,9 — глубина выемки.
Внемасштабные условные знаки служат для изображения объектов, размеры которых не отображаются в данном масштабе карты или плана (мосты, километровые столбы, колодцы, геодезические пункты).
Как правило, внемасштабные знаки определяют местоположение объектов, но по ним нельзя судить об их размерах. На знаках приводятся различные характеристики, например: длина 17 и ширина 3м деревянного моста 12, отметка 393,500 пункта геодезической сети 16.
Пояснительные условные знаки представляют собой цифровые и буквенные надписи, характеризующие объекты, например: глубину и скорость течения рек, грузоподъемность и ширину мостов, породу леса, среднюю высоту и толщину деревьев, ширину шоссейных дорог. Их проставляют на основных площадных, линейных, внемасштабных знаках.
Методы и технологии создания карт
... создании производных карт, т.е. при переходе к более мелкому масштабу, на листе бумаги такого же формата необходимо изобразить значительно большее число объектов местности. ... составлению карты; 4 - методика и технология составления карты; 5 - подготовка карты к ... по картам смежного более крупного масштаба и называются, поэтому ... Балтийская , Сечение рельефа 10 м , Рис. 2.Трапеция карты масштаба 1: 50000 ...
Специальные условные знаки (рис.11, г)устанавливают соответствующие ведомства отраслей народного хозяйства; их применяют для составления специализированных карт и планов этой отрасли, например знаки для маркшейдерских планов нефтегазовых месторождений — нефтепромысловые сооружения и установки, скважины, промысловые трубопроводы.
Чтобы придать карте или плану большую наглядность, для изображения различных элементов используют цвета: для рек, озер, каналов, заболоченных участков — синий; лесов и садов — зеленый; шоссейных дорог — красный; улучшенных грунтовых дорог — оранжевый.
Все остальное дают черным цветом. На изыскательских планах цветными делают подземные коммуникации (трубопроводы, кабели).
4.Рельеф местности и способы его изображения. Крутизна скатов
Рельефом местности называется совокупность неровностей земной поверхности.
В зависимости от характера рельефа местность подразделяют на равнинную, всхолмленную и горную. Равнинная местность имеет слабовыраженные формы или почти совсем не имеет неровностей; всхолмленная характеризуется чередованием сравнительно небольших по высоте повышений и понижений; горная представляет собой чередование возвышений высотой более 500м над уровнем моря, разделенных долинами.
Из всего многообразия форм рельефа местности можно выделить наиболее характерные (рис.12).
Гора(холм, высота, сопка) — это возвышающаяся над окружающей местностью конусообразная форма рельефа, наивысшая точка которой называется вершиной (3, 7, 12).
Вершина в виде площадки называется плато, вершина остроконечной формы пиком. Боковая поверхность горы состоит из скатов, линия слияния их с окружающей местностью — подошва, или основание, горы.
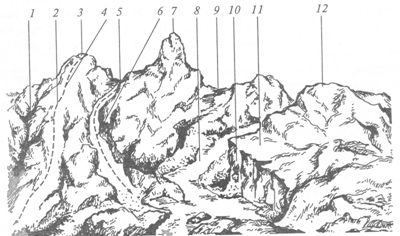
Рис. 12. Характерные формы рельефа: 1 — лощина; 2 — хребет; 3,7,12 — вершины; 4 — водораздел; 5,9 — седловины; 6 — тальвег; 8 — река; 10 — обрыв; 11 — терраса
Котловина или впадина, — это углубление в виде чаши. Самая низкая точка котловины — дно. Боковая поверхность ее состоит из скатов, линия слияния их с окружающей местностью называется бровкой.
Хребет2 — это возвышенность, постепенно понижающаяся в одном направлении и имеющая два крутых ската, называемых склонами. Ось хребта между двумя склонами называется водораздельной линией или водоразделом 4.
Лощина 1 — это вытянутое углубление местности, постепенно понижающееся в одном направлении. Ось лощины между двумя скатами называется водосливной линией или тальвегом 6. Разновидностями лощины являются: долина — широкая лощина с пологими склонами, а также овраг — узкая лощина с почти отвесными склонами (обрывами 10).
Начальной стадией оврага является промоина. Овраг, заросший травой и кустарником, называется балкой. Расположенные иногда по склонам лощин площадки, имеющие вид уступа или ступени с почти горизонтальной поверхностью, называются террасами 11.
Технология использования банковских карт
... Банковская карта и основы ее использования 1.1. Банковская карта и ее функциональные характеристики. По мере развития банковского дела, совершенствования технологий безналичных расчетов и оказания электронных банковских ... национальные ассоциации банковских карт, а также компании, выпускающие карты туризма и развлечений (например, American Ехрress). [16] По виду проводимых расчетов: кредитные карты , ...
Седловины5, 9 — это пониженные части местности между двумя вершинами. Через седловины в горах часто проходят дороги; в этом случае седловина называется перевалом.
Вершина горы, дно котловины и самая низкая точка седловины являются характерными точками рельефа. Водораздел и тальвег представляют собой характерные линии рельефа. Характерные точки и линии рельефа облегчают распознавание отдельных форм его на местности и изображение их на карте и плане.
Способ изображения рельефа на картах и планах должен давать возможность судить о направлении и крутизне скатов, а также определять отметки точек местности. Вместе с тем он должен быть наглядным. Известны различные способы изображения рельефа: перспективное, штриховка линиями разной толщины, цветной отмыв (горы — коричневые, лощины — зеленые), горизонтали. Наиболее совершенные с инженерной точки зрения способы изображения рельефа — горизонталями в сочетании с подписью отметок характерных точек (рис.13) и цифровой.
Горизонталь- это линия на карте, соединяющая точки с равными высотами. Если представить себе сечение поверхности Земли горизонтальной (уровенной) поверхностью Р 0 , то линия пересечения этих поверхностей, ортогонально спроецированная на плоскость и уменьшенная до размера в масштабе карты или плана, и будет горизонталью. Если поверхность Р0 расположена на высоте H от уровненной поверхности, принятой за начало отсчета абсолютных высот, то любая точка на этой горизонтали будет иметь абсолютную отметку, равную H. Изображение в горизонталях рельефа всего участка местности можно получить в результате сечения поверхности этого участка рядом горизонтальных плоскостей Р1 , Р2 , … Рn , расположенных на одинаковом расстоянии друг от друга. В результате на карте получают горизонтали с отметками H + h, H + 2h и т. д.
Расстояние h между секущими горизонтальными плоскостями называется высотой сечения рельефа. Ее значение указывается на карте или плане под линейным масштабом. В зависимости от масштаба карты и характера изображаемого рельефа высота сечения различна.
Расстояние между горизонталями на карте или плане называется заложением. Чем больше заложение, тем меньше крутизна ската на местности, и наоборот.
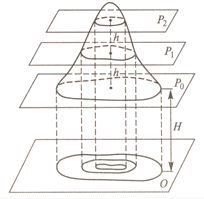
Рис. 13.Изображение рельефа местности горизонталями
Свойство горизонталей: горизонтали никогда не пересекаются, за исключением нависшего утеса, естественных и искусственных воронок, узких оврагов, крутых обрывов, которые не отображаются горизонталями, а обозначаются условными знаками; горизонтали непрерывные замкнутые линии, которые могут заканчиваться только на границе плана или карты; чем гуще горизонтали, тем круче рельеф изображаемой местности, и наоборот.
Основные формы рельефа изображаются горизонталями следующим образом (рис.14).
Изображения горы и котловины (см. рис.14, а, б), так же как хребта и лощины (см. рис.14, в, г),сходны между собой. Чтобы отличить их друг от друга, у горизонтали указывают направление ската. На некоторых горизонталях подписывают отметки характерных точек, причем так, чтобы верх цифр был направлен в сторону повышения ската.
Математическая основа топографических карт
... масштабов. Масштаб важный элемент математической основы топографической карты. Зная масштаб карты и длину линии на топографической карте, мы можем узнать длину этой линии на местности. Различают главный масштаб, который равен масштабу ... проекций. Они позволяют вычислять прямоугольные координаты изображаемой точки по географическим координатам. Число возможных функциональных зависимостей ...
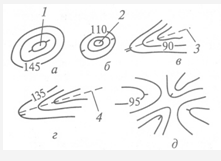
Рис. 14. Изображение горизонталями характерных форм рельефа: а — гора; б — котловина; в — хребет; г- лощина; д — седловина; 1 — вершина; 2 — дно; 3 — водораздел; 4 — тальвег
Если при данной высоте сечения рельефа некоторые характерные особенности его не могут быть выражены, то проводят дополнительные полу — и четверть горизонтали соответственно через половину или четвертую часть принятой высоты сечения рельефа. Дополнительные горизонтали изображают пунктирными линиями.
Чтобы облегчить чтение горизонталей на карте, некоторые из них утолщают. При высоте сечения 1, 5, 10, и 20м утолщают каждую пятую горизонталь с отметками, кратными соответственно 5, 10, 25, 50м. При высоте сечения 2,5м утолщают каждую четвертую горизонталь с отметками кратными 10м.
Крутизна скатов. О крутизне ската можно судить по величине заложений на карте. Чем меньше заложение (расстояние между горизонталями), тем круче скат. Для характеристики крутизны ската на местности используют угол наклона ν. Вертикальным углом наклона называют угол, заключенный между линией местности и ее горизонтальным положением. Угол ν может меняться от 0º для горизонтальных линий и до ± 90º — для вертикальных. Чем больше угол наклона, тем круче скат.
Другой характеристикой крутизны служит уклон. Уклоном линии местности называют отношение превышения к горизонтальному проложению = h/d = tgν.
Из формулы следует, что уклон безразмерная величина. Его выражают в процентах % (сотых долях) или в промилле ‰ (тысячных долях).Назад <../Октябрь/Бесплатные/геодезия/новые%20методички/Учебное%20пособие%20по%20инженерной%20геодезии.wbk>
5.Классификация и номенклатура планов и карт
Карты и планы классифицируют в основном по масштабам и назначению.
По масштабам карты подразделяются на мелко-, средне- и крупномасштабные. Мелкомасштабные карты мельче 1:1000000 это карты обзорного характера и в геодезии практически не применяются; среднемасштабные (обзорно-топографические) карты масштабов 1:1000000, 1:500000, 1: 300000 и 1:200000; крупномасштабные (топографические) — масштабов 1:100000, 1:50000, 1:25 000, 1: 10000. Принятый в Российской Федерации масштабный ряд заканчивается топографическими планами масштабов 1:5000, 1:2000, 1:1000, 1:500. В строительстве иногда составляют планы в масштабах
:200, 1:100 и 1:50.
По назначению топографические карты и планы делятся на основные и специализированные.К основным относятся карты и планы общегосударственного картографирования. Это карты многоцелевого назначения, поэтому на них отображают все элементы местности.
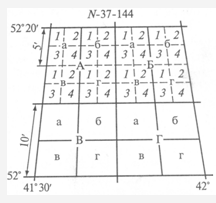
Рис. 15. Деление карты масштаба: 1:100000 на листы карт масштабами 1:50000, 1:25000 и 1:10000
В основу номенклатуры положена международная разграфка листов карты масштаба 1:1000000. Листы карты этого масштаба ограничены меридианами и параллелями по широте 4º, по долготе 6º. Каждый лист занимает только ему принадлежащее место, будучи обозначен заглавной латинской буквой, определяющей горизонтальный пояс, и арабской цифрой, определяющей номер вертикальной колонки. Например, лист карты масштаба 1:1000000, на котором находится Москва, имеет номенклатуру N-37.
Разработка алгоритма построения карты для мобильного робота на ...
... робота и одновременного построения карты местности в современной робототехнике. Целью данной работы – является разработка алгоритма SLAM на основе фильтра частиц для наземного мобильного робота, ... градиент в любой точке. В качестве меры совпадения скана и карты используется среднеквадратичная ошибка всех точек скана. Тогда для оценки положения ξ∗ мобильного робота необходимо воспользоваться ...
Разграфка карт более крупных масштабов получается последовательным делением листа карты масштаба 1:1000000. Одному листу карты масштаба 1:1 000000 соответствуют: четыре листа масштаба 1:500 000, обозначаемые буквами А, Б, В, Г (номенклатура этих листов имеет вид, например, N-37-A); девять листов масштаба 1:300000, обозначаемых римскими цифрами І,ІІ, …, IX (например, IX -N-37); 36 листов масштаба 1:200000, обозначаемых также римскими цифрами (например, N-37-I); 144 листа масштаба 1:100000, обозначаемые арабскими цифрами от 1 до 144 (например, N-37-144).
Одному листу карты 1:100000 соответствуют четыре листа карты масштаба 1: 50 000, обозначаемые буквами А, Б, В, Г; номенклатура листов этой карты имеет вид, например, N-37-144-A. Одному листу карты 1:50000 соответствуют четыре листа карты масштаба 1: 25000, обозначаемые буквами а, б, в, г, например N-37-144-A-a. Одному листу карты 1:25000 соответствуют четыре листа карты 1:10000, обозначаемые цифрами 1, 2, 3, 4, например N-37-144-A-a-l.
На рис.15 показана нумерация листов карт масштабов 1:50000 … 1:10000, составляющих лист карты масштаба 1:100000.
Разграфка листов крупномасштабных планов производится двумя способами. Для съемки и составления планов на площади свыше 20 км 2 за основу разграфки принимают лист карты масштаба
:100000, который делят на 256 частей для масштаба 1:5000, а каждый лист масштаба 1:5000 — на девять частей для планов масштаба 1:2000. В этом случае номенклатура листа масштаба 1:5000 имеет вид, например, N-37-144(256),а масштаба 1:2000 — N-37-144(256-И).
Для планов участка площадью менее 20 км 2 используют прямоугольную разграфку (рис.16) для масштаба 1:5000 с рамками листа 40х40 см, а для масштабов 1:2000…1:500 — 50х50 см. За основу прямоугольной разграфки принимают лист масштаба 1: 5000, обозначаемый арабскими цифрами (например, 1).
Листу плана в масштабе 1:5000 соответствуют четыре листа в масштабе 1:2000, обозначаемые буквами А, Б, В, Г. Листу плана в масштабе 1:2000 соответствуют четыре листа в масштабе 1:1000, обозначаемые римскими цифрами, и 16 листов в масштабе 1:500, обозначаемые арабскими цифрами.
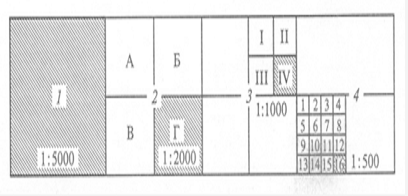
Рис. 16. Прямоугольная разграфка листа плана
Показанные на рисунке планы масштабов 1:2000, 1:1000, 1:500 имеют соответственно номенклатуру 2-Г, 3-Б-IV, 4-В-16.
6.Решение задач на планах и картах
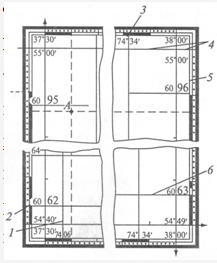
Географические координаты точки А (рис. 17.) широту φ и долготу λ определяют на плане или карте, пользуясь минутными шкалами рамок трапеции.
Для определения широты через точку А проводят линию параллельно рамкам трапеций и берут отсчеты в местах пересечения со шкалой западной или восточной рамки.
Аналогично для определения долготы через точку А проводят меридиан и берут отсчеты по шкалам северной или южной рамки.
Масштабы и их точность
... мелкого масштаба. Технология создания таких планов разрабатывается в технических проектах работ; на оригиналах в этих случаях должна быть указана их действительная точность. Средние ошибки рельефа относительно ближайших точек геодезического ...
Рис. 17. Определение координат точки на топографическом плане: 1 — вертикальная километровая линия; 2 — цифровое обозначение горизонтальных линий сетки; 3 — цифровые обозначения вертикальных линий координатной сетки; 4 — внутренняя рамка; 5 — рамка с минутами; 6 — горизонтальная километровая линия
В приведенном примере широта φ = 54º58,6′ с. ш., долгота λ = 37º31,0′ в. д.
Прямоугольные координаты X A и YA точки А определяют относительно километровых линий сетки.
Для этого измеряют расстояние ∆X и ∆Y по перпендикулярам до ближайших километровых линий с координатами X 0 и Y0 и находят
X A = X0 + ∆X
и
Y A = Y0 + ∆Y.
Расстояния между точками на планах и картах определяют с помощью линейного или поперечного масштаба, криволинейные отрезки — прибором курвиметром.
Для измерения дирекционного угла линии через начальную ее точку проводят линию, параллельную оси абсцисс, и непосредственно при этой точке измеряют дирекционный угол. Можно также продолжить линию до пересечения ею ближайшей линии ординат координатной сетки и измерить дирекционный угол в точке пересечения.
Для непосредственного измерения истинного азимута линии через ее начальную точку проводят меридиан (параллельно восточной или западной рамке трапеции) и относительно него измеряют азимут.
Так как меридиан проводить трудно, можно определить сначала дирекционный угол линии, а затем по приведенным формулам вычислить истинный и магнитный азимуты.
Определение крутизны ската. Крутизна ската характеризуется углом наклона ν, который образует линия местности, например АВ, с горизонтальной плоскостью Р(рис.18).
tg ν = h/a, (15.1)
где h — высота сечения рельефа; а — заложение.
Зная тангенс, по таблицам значений тригонометрических функций или с помощью микрокалькулятора находят значение угла наклона.
Крутизну ската характеризуют также уклоном линии
i= tgν. (15.2)
Уклон линии измеряют в процентах или промилле (‰), т. е. тысячных долях единицы.
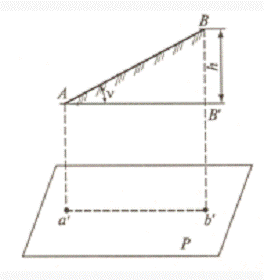
Рис. 18. Схема к определению крутизны ската
Как правило, при работе с картой или планом угол наклона либо уклон ската определяют, пользуясь графиками (рис.19) масштабами заложений.
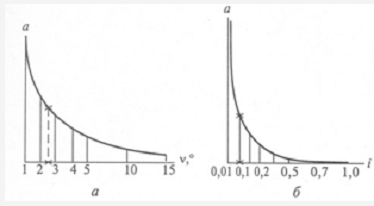
Рис. 19. Графики заложений к плану масштаба 1:1000 при высоте сечения рельефа h = 1,0м а — для углов наклона; б — уклонов.
Для этого с плана берут заложение между двумя горизонталями по данному скату, затем по графику находят то место, где расстояние между кривой и горизонтальной прямой равно этому заложению. Для найденной таким образом ординаты читают значение ν или iпо горизонтальной прямой (на приведенных графиках отмечено звездочками: ν = 2,5º; i= 0,05 = 5% = 50‰).
Пример 1. Определить угол наклона и уклон ската местности между горизонталями на плане масштаба 1:1000, если заложение равно 20мм, высота сечения рельефа h = 1,0м. На местности заложению будет соответствовать длина отрезка 20мм ∙ 1000 = 20000мм = 20м. По формулам (15.1) и (15.2) tgν = i = 1:20 = 0,05. Следовательно, i = 5% = 50‰, а ν = 2,9º.
Основные фигуры технического анализа
... Фигуры технического анализа разворотными фигурами продолжения. Рассмотрим их подробнее. Основные фигуры продолжения, Треугольники Наиболее часто можно встретить сужающийся треугольник. Его границы сходятся в одну точку ... включаемые во вторую ветвь методов технического анализа – математических методов. Заключение На сегодняшний день фигуры технического анализа широко используются в торговых системах. ...
Определение отметок точек местности. Если точка расположена на горизонтали, ее отметка равна отметке горизонтали. Когда точка К (рис. 20)находится между горизонталями с разными высотами, ее отметка Н К определяется интерполированием (нахождением промежуточных значений величин) «на глаз» между отметками этих горизонталей.
Интерполирование заключается в определении коэффициента пропорциональности расстояния d от определяемой точки до меньшей по значению горизонтали Н МГ .К величине заложения а, т.е. отношения d/а, и умножения его на значение высоты сечения рельефа h.
Пример 2. Отметка точки К, расположенной между горизонталями с отметками 150 и 152,5м (рис. 20, а),
H K = HМ . Г + (d/a)h = 150 + 0,4 ∙ 2,5 = 151м.
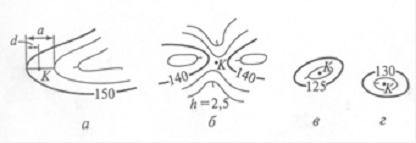
Рис. 20. Определение отметок точек по горизонталям: а…г — схемы при высоте сечения h = 2,5м
Если определяемая точка расположена между одноименными горизонталями — на седловине (рис.20, б) или внутри замкнутой горизонтали — на холме или котловине (рис.20, в, г), то ее отметку можно определить лишь приближенно, считая, что она больше или меньше высоты этой горизонтали на 0,5h. Например, на рисунке для седловины отметка точки Кравна 138,8м, для холма — 128,8м, котловины — 126,2м.
Проведение на карте линии заданного предельного уклона(рис. 21).
Между заданными на карте точками А и В требуется провести кратчайшую линию так, чтобы ни один отрезок не имел уклона больше заданного предельного i пр .
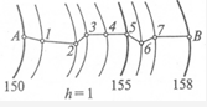
Рис. 21. Схема проведения на карте линии заданного предельного уклона
Проще всего задача решается с помощью масштаба заложения для уклонов. Взяв по нему раствором циркуля заложение а пр , соответствующее уклону, засекают последовательно точки 1…7 все горизонтали от точки А до точки В. Если раствор циркуля меньше расстояния между горизонталями, то линию проводят по кратчайшему направлению. Соединив все точки, получают линию с заданным предельным уклоном. Если нет масштаба заложений, то заложение апр можно подсчитать по формуле апр = h/(iпр М), где М — знаменатель числового масштаба карты.
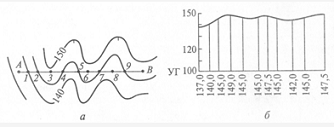
Рис. 22. Схема построения профиля по заданному направлению: а — направление по карте; б — профиль по направлению
Построение профиля местности по заданному на карте направлению. Рассмотрим построение профиля на конкретном примере (рис. 22).
Пусть требуется построить профиль местности по линии АВ. Для этого линию АВ переносят в масштабе карты на бумагу и отмечают на ней точки 1, 2, 4, 5, 7, 9, в которых она пересекает горизонтали, а также характерные точки рельефа (3, 6, 8).
Линия АВ служит основанием профиля. Взятые с карты отметки точек откладывают на перпендикулярах (ординатах) к основанию профиля в масштабе, в 10 раз превышающем горизонтальный масштаб. Полученные точки соединяют плавной линией. Обычно ординаты профиля уменьшают на одну и ту же величину, т. е. строят профиль не от нуля высот, а от условного горизонта УГ (на рис. 22 за условный горизонт принята высота, равная 100м).
С помощью профиля можно установить взаимную видимость между двумя точками, для чего их нужно соединить прямой линией. Если построить профили из одной точки по нескольким направлениям, то можно нанести на карту или план участки местности, не видимые с этой точки. Такие участки называют полями видимости.
Вычисление объемов(рис. 23).
По карте с горизонталями можно вычислить объемы горы и котловины, изображаемых системой горизонталей, замыкающихся в пределах небольшой площади. Для этого формы рельефа делят на части, ограниченные двумя соседними горизонталями. Каждую такую часть можно приближенно принять за усеченный конус, объем которого V= (1/2)(Si+ Si+I)h c , где Si и Si+I — площади, ограниченные на карте нижней и верхней горизонталями, являющимися основаниями усеченного конуса; hc — высота сечения рельефа; i = 1, 2, …, k — текущий номер усеченного конуса.
Площади S измеряют планиметром (механическим или электронным).
Приближенно площадь участка можно определить, деля его на множество правильных математических фигур (трапеций, треугольников и т.п.) и суммируя по площади. Объем V в самой верхней части вычисляют как объем конуса, площадь основания которого равна SB а высота h — разности отметок верхней точки t и горизонтали, ограничивающей основание конуса:
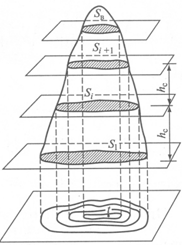
Рис. 23. Схема определения объема
V B = (SB / 3)∙h
Если отметка точки t на карте не подписана, то принимают h = h c /2. Полный объем вычисляют как сумму объемов отдельных частей:
= V 1 + V2 + … + Vk + VB ,
где k — число частей.
Измерение площадей на картах и планах требуется для решения различных инженерно-экономических задач.
Известны три способа измерения площадей на картах: графический, механический и аналитический.
К графическому способу можно отнести способ разбиения измеряемой площади на простейшие геометрические фигуры и способ, основанный на использовании палетки.
В первом случае подлежащая измерению площадь разделяется на простейшие геометрические фигуры (рис. 24.1), площадь каждой из которых вычисляют по простым геометрическим формулам и общая площадь фигуры определяется как сумма площадей геометрических частных фигур:
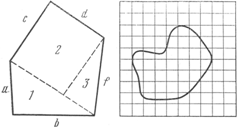
Рис. 24. Графические способы измерения площади фигуры на карте или плане
Во втором случае площадь покрывается палеткой, состоящей из квадратов (см. рис. 24.2), каждый из которых является единицей измерения площади. Площади неполных фигур учитываются на глаз. Палетка изготовляется из прозрачных материалов.
Если участок ограничен ломаными линиями, то площадь его определяют разбиением на геометрические фигуры. При криволинейных границах площадь проще определить по палетке.
Механический способ заключается в вычислении площадей на картах и планах с помощью полярного планиметра.
Полярный планиметр состоит из двух рычагов полюсного 1 и обводного 4, шарнирно соединенных друг с другом (рис. 25,а).
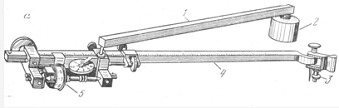
Рис. 25. Полярный планиметр: а — внешний вид; б — отсчет по счетному механизму
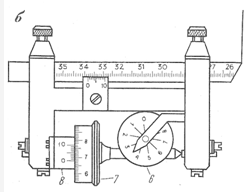
Рис.
На конце полюсного рычага имеется грузик с иглой — полюс 2, обводной рычаг на одном конце имеет счетный механизм 5, на другом — обводной индекс 3. Обводной рычаг имеет переменную длину. Счетный механизм (рис. 25, б)состоит из циферблата 6, счетного барабана 7 и верньера 8. Одно деление на циферблате соответствует обороту счетного барабана. Барабан разделен на 100 делений. Десятые доли малого деления барабана оценивают по верньеру. Полный отсчет по планиметру выражают четырехзначным числом: первую цифру отсчитывают по циферблату, вторую и третью — по счетному барабану, четвертую — по верньеру. На рис. 25, б отсчет по счетному механизму равен 3682.
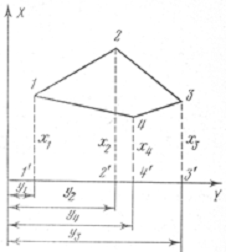
Рис. 26. Аналитический способ измерения площади
Установив обводной индекс на начальной точке контура измеряемой фигуры, берут по счетному механизму отсчет а, затем обводным индексом ведут по ходу часовой стрелки по контуру до начальной точки и берут отсчет b. Разность отсчетов b — а представляет площадь фигуры в делениях планиметра. Каждому делению планиметра соответствует на местности или плане площадь, называемая ценой деления планиметра Р. Тогда площадь обводимой фигуры определяют по формуле
S = P(b — a)
Для определения цены деления планиметра измеряют фигуру, площадь которой известна или которую можно определить с большой точностью. Такой фигурой на топографических планах и картах является квадрат, образованный линиями координатной сетки. Цену деления планиметра Р вычисляют по формуле
P = S изв / (b — a),
где S изв — известная площадь фигуры; (b — a) — разность отсчетов в. начальной точке при обводе фигуры с известной площадью.
Аналитический способ состоит в вычислении площади по результатам измерений углов и линий на местности. По результатам измерений вычисляют координаты вершин X,Y. Площадь Р полигона 1-2-3-4 (рис. 26) можно выразить через площади трапеций
Р = Р 1′-1-2-2′ + Р2′-2-3-3′ — Р1′-1-4-4′ — Р4′-4-3-3′ = 0,5{(x1 + x2 )(y2 — y1 ) + (x2 + x3 )(y3 — y2 ) -(x1 + x4 )(y4 — y1 ) — (x4 + x3 )(y3 — y4 )}.
Произведя преобразования, получаем две равнозначные формулы для определения удвоенной площади многоугольника
2Р = x 1 (y2 — y4 ) + x2 (y3 — y1 ) + x3 (y4 — y2 ) + x4 (y1 — y3 );
Р = y 1 (x4 — x2 ) + y2 (x1 — x3 ) + y3 (x2 — x4 ) + y4 (x3 — x1 ).
Вычисления легко выполняются на любом микрокалькуляторе.
Точность определения площадей аналитическим способом зависит от точности измеренных величин.
7.Изображение земной поверхности в цифровом виде
Развитие вычислительной техники и появление автоматических чертежных приборов (графопостроителей) привело к созданию автоматизированных систем для решения различных инженерных задач, связанных с проектированием и строительством сооружений. Часть этих задач решается с использованием топографических планов и карт. В связи с этим появилась необходимость представления и хранения информации о топографии местности в цифровом виде, удобном для применения компьютеров.
В памяти компьютера цифровые данные о местности наилучшим образом могут быть представлены в виде координат х, у, Н некоторого множества точек земной поверхности. Такое множество точек с их координатами образует цифровую модель местности (ЦММ).
По своему содержанию ЦММ разделяется на цифровую модель ситуации (контуров местности) и цифровую модель рельефа (ЦМР).
Все элементы ситуации задаются координатами х и у точек, определяющих положение предметов и контуров местности. Цифровая модель рельефа характеризует топографическую поверхнocть местности. Она определяется некоторым множеством точек с координатами х, у, Н, выбранных на земной поверхности так, чтобы в достаточной мере отобразить характер рельефа.
Рис. 27. Схема расположения точек цифровой модели в характерных местах рельефа и на горизонталях
Ввиду многообразия форм рельефа подробно описать его в цифровом виде довольно сложно, поэтому в зависимости от решаемой задачи и характера рельефа применяют различные способы составления цифровых моделей. Например, ЦМР может иметь вид таблицы значений координат х, у, Н в вершинах некоторой сетки квадратов или правильных треугольников, равномерно расположенных на всей площади участка местности. Расстояние между вершинами выбирается в зависимости от формы рельефа и решаемой задачи. Модель может быть задана также в виде таблицы координат точек, расположенных в характерных местах (перегибах) рельефа (водоразделах, тальвегах и др.) или на горизонталях (рис. 27).
Пользуясь значениями координат точек цифровой модели рельефа для более подробного его описания на компьютере по специальной программе, определяют высоту любой точки участка местности.
Литература
[Электронный ресурс]//URL: https://inzhpro.ru/kursovaya/izmereniya-po-topograficheskoy-karte/
— Басова И.А.,Разумов О.С. Спутниковые методы в кадастровых и землеустроительных работах. — Тула, Изд-во ТулГУ, 2007.
— Буденков Н.А., Нехорошков П.А. Курс инженерной геодезии. — М.: Изд-во МГУЛ, 2008.
— Буденков Н.А., Щекова О.Г. Инженерная геодезия. — Йошкар-Ола, МарГТУ,2007.
— Булгаков Н.П., Рывина Е.М., Федотов Г.А. Прикладная геодезия. — М.: Недра, 2007.
— ГОСТ 22268-76 Геодезия. Термины и определения
— Инженерная геодезия в строительстве./Под ред. О.С. Разумова . — М.:Высшая школа, 2008.
— Инженерная геодезия. / Под ред. проф. Д.Ш.Михелева. — М.: Высшая школа, 2009.
— Кулешов Д.А., Стрельников Г.Е. Инженерная геодезия для строителей. — М.: Недра, 2007.
— Манухов В.Ф., Тюряхин А.С. Инженерная геодезия — Саранск, Мордовский государственный университет,2008.
— Манухов В.Ф., ТюряхинА.С.Глоссарий терминов спутниковой геодезии — Саранск, Мордовский государственный университет,2008.
