Большинство математических понятий прошли долгий путь развития. Сложный путь прошло и понятие функция. Данная зачетная работа посвящена знакомству с историей возникновения понятия функции и изучению этого понятия в школьном курсе математики.
Основные цели:
— выявить ключевые моменты в определении этого понятия, на которые необходимо обратить особое внимание при изучении данной темы;
- показать связь функции с закономерностями природы;
- совершенствовать навыки исследовательской деятельности.
Задачи реферата:
- повторить и обобщить понятие функции, ее свойства;
- расширить кругозор учащихся;
- повысить уровень математической культуры.
В школьной литературе преобладает традиционная методика изложения понятия функции. В результате учащиеся не могут ответить на элементарные вопросы, относящиеся к этой теме. В данном реферате представлена история возникновения понятия, различные трактовки понятия функции из истории и школьной литературы, вопросы, связанные со способами задания функции, классы функций, свойства функций, способы преобразования графиков функций, связь понятия функции с различными областями наук.
Важной составляющей при изучении понятия является наглядная иллюстрация характерных свойств функции. Реферат содержит разработку урока по теме «Квадратичная функция» и математическую викторину по теме «Звездный час функции».
В процессе работы над рефератом была проанализирована основная литература по данной теме, список которой приводится в конце. Среди этой литературы на мой взгляд пособие для учителей «История математики в школе» Г.И.Глейзера в полной мере дает представление об истории возникновения понятия. Справочное пособие для вузов Р.Б. Райхмиста « Графики функций» в наибольшей степени соответствует современным требованиям изучения понятия функции.
В данной работе сделана попытка собрать материал по данной теме, систематизировать его для того, чтобы выделить важные моменты при формировании понятия функции и препятствовать формальному усвоению понятий, сопутствующих определению функции. Данный реферат содержит много материала, связанного с понятием функции в школьном курсе, дает возможность понять, что функция играет важную роль в практической деятельности человека.
2. Из истории математики., Понятие функция уходит корнями в
С развитием скотоводства, земледелия, ремесел и обмена увеличилось количество известных людям зависимостей между величинами. Идея зависимости некоторых величин восходит, по-видимому, к древнегреческой науке.
История кинематики. Основные понятия кинематики
... в ходе которых была открыта кинематика. 3. Ознакомиться с основными понятиями кинематики. 1. История кинематики Аристотель - древнегреческий учёный, ... не установлено. 1.4 Ученые, выделившие отдельный раздел механики кинематика аристотель механика вариньон Хочется отметить, что не только ... (векторный способ), проведенного из начала координат до данной точки (рис. 1). Рис. 1 Определение положения ...
Сам термин «функция» возник лишь в 1664 году в работах немецкого ученого Лейбница. Но Лейбниц все-таки оставался в круге геометрических представлений. Только ученик Лейбница Бернулли дал в 1718 году определение функции, свободное от геометрических образов.
С проблемой общего определения функции в середине XVIII века столкнулись крупнейшие математики того времени, Жан ле Рон Даламбер и Леонард Эйлер, в решении задачи о колебаниях струны. В спор с ними ввязался молодой математик, сын Иоганна Бернулли, Даниил Бернулли. Но в их формулировках еще ничего не говорилось о допустимом характере зависимости «первых» величин от «вторых», они оставались достаточно расплывчатыми, так что каждый из последующих математиков был волен истолковывать их на свой лад. Свою лепту внесли Сильвестр Франсуа Лакруа, Жозеф Фурье, Коши, Николай Иванович Лобачевский, Петер Лежен Дирихле. Математики даже разбились на два лагеря – сторонников определения функции «по Дирихле», не требующих обязательного правила, и сторонников определения функции «по Лобачевскому», требующих обязательного правила из конечного числа слов.
В конце двадцатых годов прошлого века над определением функции возникла новая угроза, теперь уже со стороны физиков. Теория явлений в физике микромира, новая эпоха в развитии новой физики, потребовала введения нового объекта – «дельта-функции». Здесь возникли очень серьезные разногласия между физиками и математиками, и тем значительнее представляется заслуга советского математика С.Л. Соболева, который открыл класс объектов, удовлетворяющих всем выдвинутым требованиям; впоследствии они были названы «обобщенными функциями».
Последняя форма определения функции еще не означает конца ее истории. Можно не сомневаться, что в дальнейшем под воздействием новых требований как самой математики, так и других наук – физики, биологии, науки об обществе, определение функции будет изменяться и каждое следующее изменение будет открывать новые горизонты науки и приводить к важным открытиям.
ОПРЕДЕЛЕНИЯ ФУНКЦИИ
Функция переменной величины есть аналитическое выражение, составленное из этой величины и постоянных. И. Бернулли, 1718.
Функция есть кривая, начертанная свободным влечением руки. Л. Эйлер, 1748.
Когда некоторые количества зависят от других таким образом, что при изменении последних изменяются и первые, то первые называются функциями вторых. Л. Эйлер, 1755.
Всякое количество, значение которого зависит от одного или многих других количеств, называется функцией этих последних, независимо от того, известно или нет, какие операции нужно произвести, чтобы перейти от них к первому.
С. Лакруа, 1797.
Функция от x есть число, которое дается для каждого x и вместе с x постепенно изменяется. Значение функции может быть дано и аналитическим выражением, или условием, которое подает средство испытывать все числа. Зависимость может существовать и оставаться неизвестной. Н.И. Лобачевский, 1834.
Оборудование металлообрабатывающее и деревообрабатывающее показатели ...
... методических рекомендаций [3]. 6.2 Определение экспериментальных значений показателей при испытаниях. 6.2.1 Экспериментальные (фактические) значения показателей энергетической эффективности металлообрабатывающего и деревообрабатывающего оборудования определяются при испытаниях этого оборудования (приемочных, на производительность, сертификационных) ...
Y есть функция от x, если всякому значению x соответствует вполне определенное значение y, причем совершенно неважно, каким именно способом установлено указанное соответствие. П. Дирихле, 1837.
Знание законов природы дало человеку возможность объяснить и предсказать ее разнообразнейшие явления.
« Математическими портретами» закономерностей природы и служит функция.
Если мы будем рисовать ряд окружностей, все более и более увеличивая их радиус, то и сама окружность будет также увеличиваться. Следовательно, длина окружности зависит от радиуса. В математике всякое правило, устанавливающее подобное соответствие, называют функцией.
Почему мы обозначаем функцию символом
3. Различные трактовки понятия функции в курсе математики.
Функция — одно из фундаментальных понятий математики, а функциональная идея является одной из определяющих идей развития школьного курса математики.
В настоящее время существуют различные трактовки общего понятия функции. В математике известны два направления. Примером первого направления является следующее: « зависимость одной переменной от другой, при которой каждому значению независимой переменной соответствует единственное значение зависимой переменной, называют функциональной зависимостью или функцией. Независимую переменную иначе называют аргументом, а о зависимой переменной говорят, что она является функцией от такого аргумента». ( Алгебра, учебник для седьмого класса общеобразовательных учреждений, под редакцией С.А. Теляковского).
Другое определение позволяет расширить понятие функции: с одной стороны функция истолковывается как соответствие, по которому для любого х из множества Х сопоставляется вполне определенное единственное у из множества У. С другой стороны функция определяется как соответствие между множествами Х и У. Говорят, что функция f отображает множество Х на множество У, принимающая значение из У ( Р.Б. Райхмист « Графики функций», М. « Высшая школа»).
Множество X всех допустимых действительных значений независимой переменной x, при которых функция y = f (x) определена, называется областью определения функции.
Множество Y всех действительных значений y, которые принимает функция, называется областью значений функции.
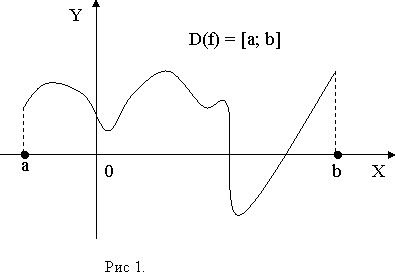
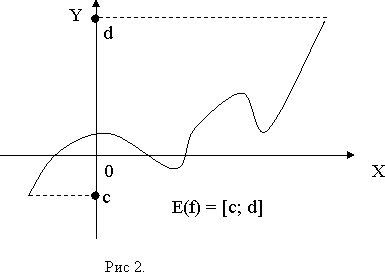
Функция считается заданной, если:
задана область определения функции X ;
- задана область значений функции Y ;
известно правило (закон) соответствия, причем такое, что для каждого значения аргумента может быть найдено только одно значение функции. Это требование однозначности функции является обязательным.
Задать функцию- это значит указать область ее определения и соответствие ( правило), при помощи которого по данному значению аргумента находятся соответствующие ему значения функции.
Занимает важное место в курсе алгебры. Она богата по содержанию, ...
... деятельности будут использованы ИКТ. Основной целью работы является разработка технологий применения компьютера в методике изучения темы «Рациональные дроби» в школе. Для решения проблемы изучения, проверки достоверности гипотезы и достижения цели реализуются следующие ...
4.Способы задания функций., Существуют разные способы задания функций., . Аналитический способ.
Аналитический способ — это наиболее часто встречающийся способ задания функции. Заключается он в том, что функция задается формулой, устанавливающей, какие операции нужно произвести над х, чтобы найти у. Например .
![]()
Рассмотрим первый пример
![]()
Здесь значению x = 1 соответствует, Функция может быть задана на разных частях множества X разными функциями., Например:
![]()
Во всех ранее приведенных примерах аналитического способа задания, функция была задана явно. То есть, справа стояла переменная y, а справа формула от переменной х. Однако, при аналитическом способе задания, функция может быть задана и неявно.
Например ![]()
Здесь, если мы задаем переменной x значение, то, чтобы найти значение переменной у (значение функции), мы должны решить уравнение. Например, для первой заданной функции при х = 3, будем решать уравнение:
![]()
То есть, значение функции при х = 3 равно -4/3.
При аналитическом способе задания, функция может быть задана параметрически — это, когда х и у выражены через некоторый параметр t. Например,
![]()
Здесь при t = 2, x = 2, y = 4. То есть, значение функции при х = 2 равно 4.
Аналитический способ является самым распространенным способом задания функций. Компактность, лаконичность, возможность вычисления значения функции при произвольном значении аргумента из области определения, возможность применения к данной функции аппарата математического анализа — основные преимущества аналитического способа задания функции. К недостаткам можно отнести отсутствие наглядности, которое компенсируется возможностью построения графика и необходимость выполнения иногда очень громоздких вычислений. Представление о функции как о некоторой формуле, связывающей х и у, к сожалению часто встречается у школьников. Одно дело функция как отображение одного множества на другое, другое дело формула, представляющая собой лишь один из способов задания функции. Такое отождествление опасно тем, что не всякая формула задает функцию, не всякую функцию можно задать с помощью формулы, несколько формул задают одну и ту же функцию.
2. Графический способ.
При графическом способе вводится прямоугольная система координат и в этой системе координат изображается множество точек с координатами (x,y).
Техническое задание дипломную работу
... специалисты, должны понимать, что при создании технического задания на свои разработки, они должны придерживаться существующих стандартов. Актуальность настоящего дипломного проекта заключается в том, что в ... услуги по автоматизации этих функций, путем создания программного продукта. Так начинается технологический процесс разработки программного обеспечения. В ходе выполнения работ должен быть решен ...
При этом у= f (х).
Пример:
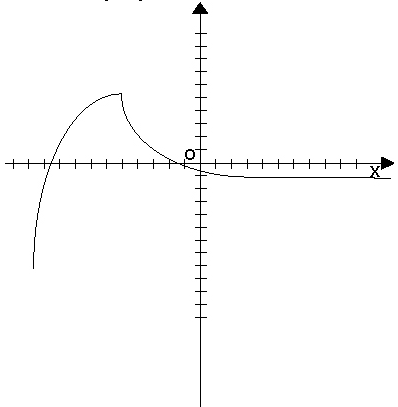
Графический способ задания функции не всегда дает возможность точно определить численные значения аргумента. Однако он имеет большое преимущество перед другими способами — наглядность. В технике и физике часто пользуются графическим способом задания функции, причем график бывает единственно доступным для этого способом.
3. Словесный способ., Функция задается с помощью словесной формулировки. Классический пример – функция Дирихле.
Птимер : функция Дирихле. «Функция равна 1, если х – рациональное число; функция равна 0, если х – иррациональное число».
Основными недостатками словесного способа задания функции являются невозможность вычисления значений функции при произвольном значении аргумента и отсутствие наглядности. Главное преимущество же заключается в возможности задания тех функций, которые не удается выразить аналитическим способом.
4. Табличный способ.
Табличный способ наиболее удобен, когда множество Х конечно. При этом способе составляется таблица, в которой каждому элементу из множества Х, ставится в соответствие число Y.
Пример:

Табличный способ задания функции очень удобен при обработке результатов исследований. Например, при выявлении зависимости между уровнем загрязнения окружающей среды.
5. Основные свойства функций.
1 Монотонность.
если для любых x1 и x2 из условия x2 > x1 следует f (x2)< f (x1),то функция f (x ) называется убывающей.
Функция, которая только возрастает или только убывает, называется монотонной.
2. Ограниченность.
Функция называется ограниченной, если существует такое положительное число M, что |f ( x )| M для всех значений x .
Если такого числа не существует, то функция — неограниченная.
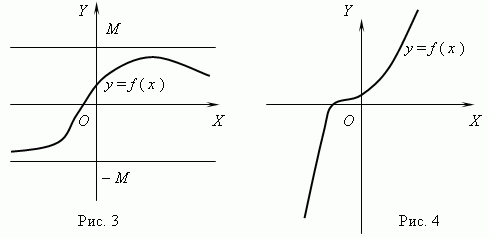
3. Непрерывность., Функция y = f (x) называется непрерывной в точке x = a, если :
функция определена при x = a, т.e. f (a) существует;
- существует конечный предел limf(x);
- f (a) = limf(x) .
Если не выполняется хотя бы одно из этих условий, то функция называется разрывной в точке x = a.
Если функция непрерывна во всех точках своей области определения, то она называется непрерывной функцией.
4. Четность и нечетность.
Если для любого x из области определения функции имеет место: f ( — x ) = f ( x ), то функция называется чётной;
если же имеет место: f (-x) = — f (x), то функция называется нечётной.
Строение и свойства металлов
... и щелочей. ^ Физические и химические свойства металлов. 1. Физические и химические свойства. Цвет. Металлы непрозрачны, т.е. не пропускают сквозь себя ... свойства. Некоторые сплавы железа и при комнатной температуре не являются ферромагнитными. Все прочие металлы разделяются на парамагнитные (притягивают магнитами) и диамагнитные (отталкиваются магнитами). Теплопроводность. Теплопроводность называется ...
График чётной функции симметричен относительно оси Y ( рис.5 ),
a график нечётной функции симметричен относительно начала координат ( рис.6 ).
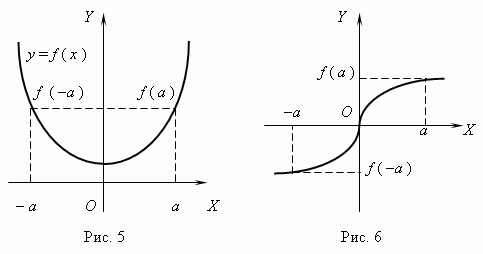
Если функция не удовлетворяет ни одному из этих условий, то она является ни четной, ни нечетной.
5. Периодичность.
Многие важные процессы в природе и технике являются периодическими, т.е. повторяющимися по истечении некоторого промежутка времени. Такие периодически повторяющиеся процессы описываются периодическими функциями. Поэтому особенно важно правильное понимание определения периодической функции.
Функция f(x) — периодическая, если существует такое отличное от нуля число T,
что для любого x из области определения функции имеет место: f ( x + T ) = f ( x ).
Такое наименьшее число называется периодом функции.
Число Т называется главным периодом, если оно положительно и является наименьшим среди всех положительных периодов, т.е. из положительных периодов функции y = f(x) (если он существует) называют её основным (главным периодом).
Пример №1. Функция y ={x} ({x} — дробная часть числа х) — периодическая. Заметим, что по определению = х — [х], где [x] — целая часть числа х. Область определения данной функции — вся числовая прямая, поэтому для любого действительного числа х и любого Tx, Т0 числа (х + Т) и (х — Т) принадлежат области определения рассматриваемой функции и f(x +T ) = {x+T} = x + T — [x + T] = x + T -([x] + T) = x + T — [x] — T = x — [x] = {x}, где Т Z, T0.
Таким образом, функция у = {x} — периодическая с периодом Т, где Т Z, T0.
Наименьшее целое положительное число равно единице. Следовательно, основной период данной функции Т = 1.
Все тригонометрические функции являются периодическими.
6.Значение аргумента, при котором функция равна 0, называется нулём (корнем) функции., Функция может иметь несколько нулей., Например, функция y = x (x + 1)(x-3) имеет три нуля: x = 0, x = — 1, x =3., Геометрически нуль функции – это абсцисса точки пересечения графика функции с осью Х ., На рис.7 представлен график функции с нулями: x = a, x = b и x = c
-
Если график функции неограниченно приближается к некоторой прямой при своём удалении от начала координат, то эта прямая называется асимптотой .
6. Свойства функций в пословицах и поговорках.
Чтобы наглядно проиллюстрировать характерные свойства функции, обратимся к пословицам. Ведь пословицы- это тоже отражение устойчивых закономерностей, выверенных многовековым опытом народа.
-
« Чем дальше в лес, тем больше дров». Изобразим графиком, как нарастает количество дров по мере продвижения в глубь леса- от опушки, где давным давно все собрано, до чащи, куда еще не ступала нога заготовителя.
18 стр., 8577 слов«МЕТОДИКА ОБУЧЕНИЯ КВАДРАТИЧНОЙ
... Полноценно тему «Квадратичная функция» проходят в 9 классе. Изучать данную тему учащиеся начинают уже имея некоторый опыт: они уже владеют рядом алгебраических функций, их свойствами, умением построения графиков функций (линейная функция, гипербола, кубическая парабола, квадратичная парабола, заданная ...
-
Горизонтальная черта – это лесная дорога. По вертикали будем откладывать количество топлива на данном километре дороги.
2. Сходное свойство иллюстрирует и пословица « Каши маслом не испортишь!».
3. « Дальше от кумы- меньше греха». Монотонно убывающая функция.
4. « Выше меры конь не скачет». Если изобразить траекторию скачущего коня, то высота скачков в полном соответствии с пословицей будет ограничена сверху некоторой «мерой».
5. « Пересев хуже недосева».
Наглядным примером периодической функции является рассказка: « У попа была собака, он ее любил и т.д. Периодичностью в обычной речи называют повторяемость. Примеры периодических функций:
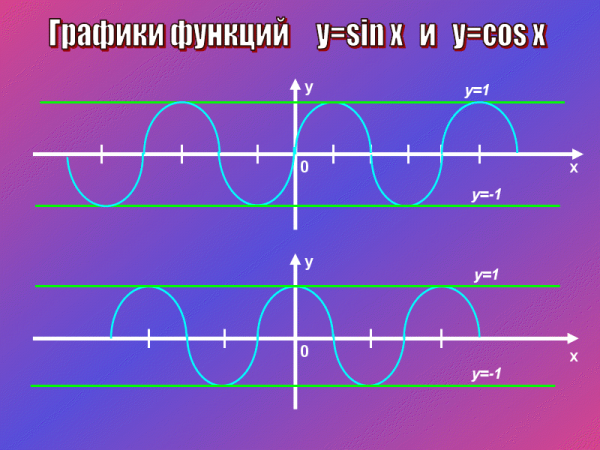
7.Функция в различных областях деятельности человека.
Каждая область знаний имеет свои объекты изучения, устанавливает свойства и взаимосвязь между этими объектами. Понятие функции и ее графика дают наглядное представление многих исследований.
Например: почему летом теплее, а зимой холоднее?
Поток энергии, идущий от солнца, одинаков во все времена года. Но в зависимости от наклона солнечных лучей, она по-разному распределяется по земной поверхности. Чем меньше угол, который образуют лучи с поверхностью, тем меньше их приходится на тот же участок. Именно эта зависимость является функциональной зависимостью. Здесь мы встречаемся с периодической функцией.
Еще пример: золотое правило механики. « Во сколько раз выиграешь в силе, во столько же раз проиграешь в расстоянии». Линия, выражающая эту зависимость- гипербола.
Бросая камень в воду, нужно смотреть на образованные круги. Такое явление природы описано функцией Бесселая. 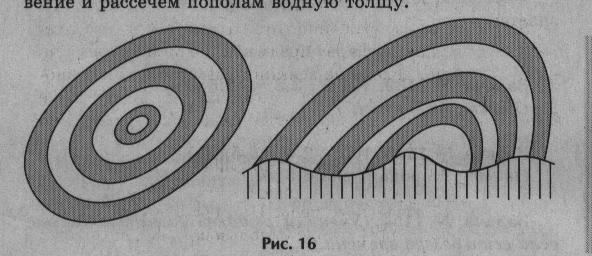
В метеорологии фиксируют изменение температуры в течении суток. Записывают эти данные в виде таблицы, потом переносят их на координатную плоскость. Чертят линию и называют графиком температуры. Такие графики ученные получают с помощью специального прибора- термографа, отмечающего температуру на движущейся ленте.
В медицине врачи выявляют болезни сердца, изучая полученные с помощью кардиографа кардиограммы.
Используются различные графики и в экономике. Поговорка чем больше пушек- тем меньше масла. Имеются в виду возможности производства в одной стране продовольствия и вооружения. Верность поговорки подтверждают и математические расчеты.
Современная математика знает множество функций, и у каждой свой « неповторимый облик», как неповторим облик каждого из миллиардов людей, живущих на Земле.
8. Разработка математической викторины «Звездный час функции»., Цель викторины
Эта викторина предлагается учащимся 10-11 классов. Участвуют две команды по 6 человек, остальные болельщики.
Построение графиков функций
... автоматически откроется главное окно программы. В колонке «Выбор функции графика» находятся 9 функций графиков, выбрать можно только 1 функцию (по умолчанию выбрана первая функция). При нажатии на главном ... ресурсов и организуют взаимодействие аппаратуры компьютера с пользователем, выполнение поставленных пользователем задач. Версия windows 7 - операционная система семейства Windows NT, следующая за ...
Вступление.
Функция – это одно из математических и общенаучных понятий. Она выражает зависимость между переменными величинами.
На нашей встрече мы постараемся вспомнить основные свойства функций, исследование и применение в различных областях науки. И еще мы постараемся доказать, что математику не зря называют «царицей наук», что ей больше, чем какой-либо науке, свойственны красота, гармония, изящность и точность. Всем математикам, говорят, присуща дерзость ума; математик не любит, когда ему о чем-нибудь рассказывают, он хочет дойти до всего сам Так что дерзайте, играйте и выигрывайте!
Конкурсы
Задание1 . Из истории математики
Учащимся предлагается плакат с портретами шести математиков, среди которых обязательно должны быть портреты Л. Эйлера, Г. Кантора, Г. Лейбница.
Ведущий:
Как известно, начиная с 17 века, одним из основных понятий в математике является функция.
1вопрос. Назовите имя одного из крупнейших математиков своего времени, члена Петербургской Академии наук, внесшего огромный вклад в развитие понятия функции, учителя Михаила Васильевича Ломоносова.
2 вопрос. О ком идет речь в следующих строках: « Он был философом и лингвистом, историком и биологом, дипломатом и политическим деятелем, математиком и изобретателем. Он мечтал о создании всемирной академии наук, о построении «универсальной науки». Он первым ввел понятие функции.
3 вопрос. Назовите имя ученого, с чьим именем связывают развитие понятия « функция» 20 веке.
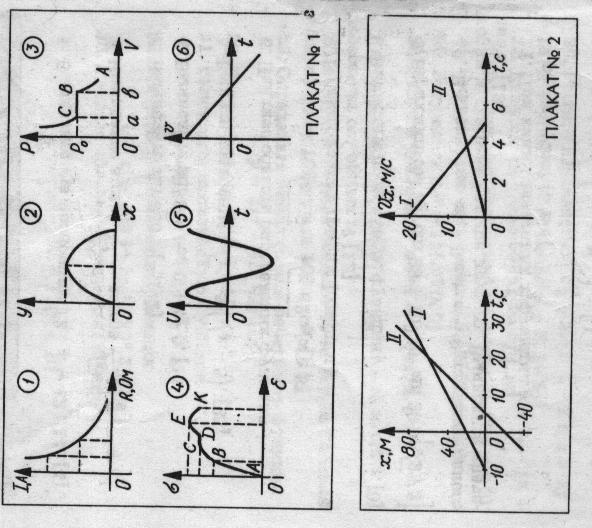
Задание 2 : Чтение графиков.
( Используется плакат № 1)
Ведущий:
Очень часто в своей практической деятельности приходится решать задачи на так называемое «чтение» графиков, т.е. по заданному графику функции у= f (х) нужно перечислить основные свойства этой функции, определить зависимость, которую выражает данный график.
1 вопрос. Среди предложенных 6 графиков функции указать тот, который выражает диаграмму растяжения физического тела.
2 вопрос. Какой из графиков является графиком движения тела, брошенного под углом к горизонту?
3 вопрос. Какой из графиков является графиком изменения напряжения в цепи переменного тока?
Задание 3., Учащимся предлагаются графики движения даух тел на миллиметровой бумаге .
Ведущий:
Вспомните, как называется раздел физики, который отвечает на вопрос: где, в какой момент времени будет находится данное тело?
Кинематика, верно. В кинематике часто пользуются графиками движения различных тел, с их помощью определяют все неизвестные кинематические величины.
Вам даны графики движения тел.Дайте характеристику движения каждого тела, используя как можно больше данных.
Функции инженера-технолога машиностроительного предприятия
... опытные инженеры в аппарате главного технолога. Служба ... по сложности работ. Устанавливают порядок выполнения работ и ... линейных и сетевых графиков, в отработке изделий ... функций бюро и отделов ОГК Конструкторские отделы разрабатывают эскизы, технические и рабочие проекты изделий, используя средства автоматизации проектирования, обеспечивают соответствие разрабатываемых конструкций техническим заданиям, ...
Время выполнения задания 5 минут., Для болельщиков задание 1.» Аукцион».
Назовите как можно больше математических терминов на букву «П». ( Последний, кто называет термин, получает приз).
Задание 4 . Построение графика функции.
Учащиеся получают карточку с заданием, где перечислены свойства функции.На большом листе миллиметровой бумаги фломастером они должны выполнить построения.
Ведущий: функциональную зависимость между различными величинами можно задать различными способами: формулой, таблицей, соответствием в виде графика. График функции можно построить, используя его функцию.
Задание.Постройте график функции, используя его свойства., Время выполнения задания 10 минут., Для болельщиков задание 2.
« Отгадайте слово».
Какую траекторию движения будет иметь камешек, застрявший в протекторе автомобиля? ( циклоида), Задание 5.
Ведущий: как мы уже говорили, понятие функция используется в различных науках. Гафически можно выразить любую функциональную зависимость. Изобразите с помощью графика смысл следующих поговорок:
-
Чем дальше в лес, тем больше дров.
-
Выше меры конь не прыгнет.
-
Пересев хуже недосева.
Графики нужно изображать на миллиметровой бумаге., Для болельщиков задание3.
Назовите имя ученого, который ввел основные законы движения всех тел, в том числе и небесных. Его именем названы эти законы. Дайте формулировку этих законов. Что вы можете сказать об этом ученом? ( Ньютон)
Задание 6.
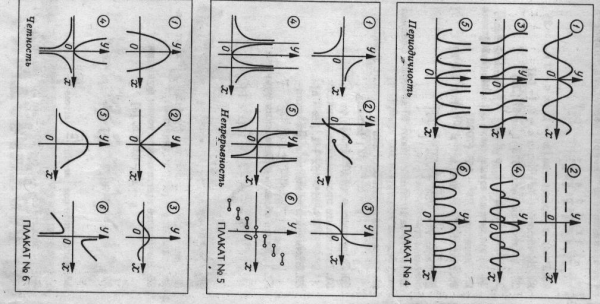
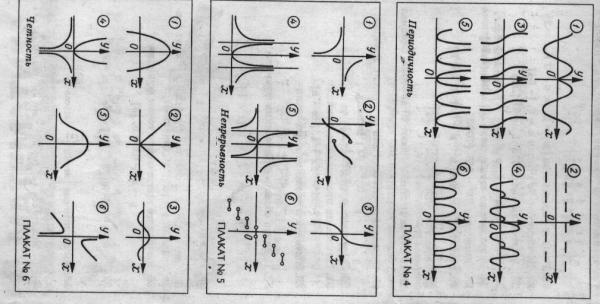
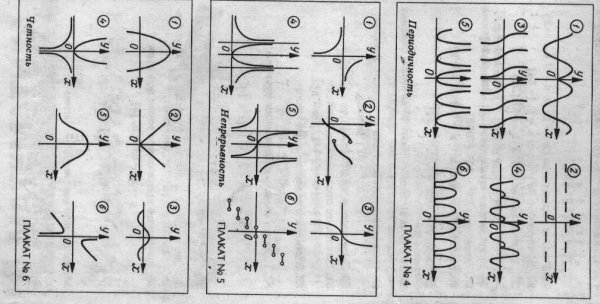
( Используются плакаты 4,5,6)
Ведущий: функции обладают можеством различных свойств, , исследуя ту или иную функцию, мы отмечаем их наличие или отсутствие.
Вопрос.Среди данных 6 функций укажите номер той, которая не отвечает свойству остальных пяти.
После окончания игры подводятся итоги, нагрждаются победители., Разраблтка урока по теме: « Квадратичная функция».
Цель урока:
1) расширение и углубление представлений учащихся о квадратичной функции;
2) развитие умения самостоятельно приобретать новые знания; использовать для достижения поставленной задачи уже полученные знания;
3) развитие самостоятельности и творчества;
4) Развитие умения определять свойства квадратичных функций;
5) формирование графических навыков учащихся.
« Природа говорит языком математики: буквы этого языка- круги, треугольники и иные математические фигуры».
Г. Галилей
Данный урок проводится в 9 классе. Предварительно учащиеся делятся на 4 группы. Выдвигантся гипотеза:
Квадратичная функция играет важную роль в жизни человека.
В течении недели ребята собирают материал по темам, которые им предоставил учитель. На уроке они должны подтвердить или опровергнуть гипотезу.Каждая группа должна приготовить резюме и визитную карточку квадратичной функции.
Тема 1:
1 Об одной из математических моделей., Квадратичная функция, Цель: получение знаний о применении квадратичной функции в природе.
Адрес: Алгебра 9 класс, параграф 3, п.5, стр.28
Дата и место рождения:, Опыт работы:, Дополнительная информация:

Гарфик квадратичной функции парабола., История возникновения и применения конических сечений
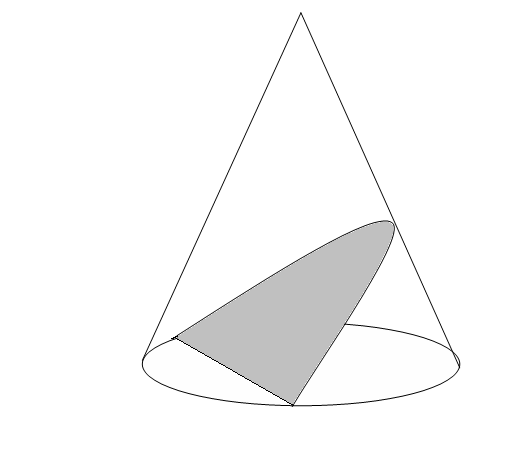
Интересным способом изучения математики являются математические модели. Пример тому – конические сечения: эллипс, гипербола и парабола. Они были открыты Аполлонием Пергским в Древней Греции. Почти 2 тыс. лет казалось, что теория конических сечений применима только к решению чисто математических задач.
Философ и Математик Рене Декарт
После того как Р. Декарт ввел понятие координатной плоскости, оказалось возможным записать каждую линию на плоскости уравнением.

Роль конических сечений в науке
Кривые второго порядка часто фигурируют при математическом описании законов природы. Планеты движутся по кривым, называемым эллипсами. Кометы же могут двигаться как по очень вытянутым эллипсам, так и по параболам или гиперболам. То, что кометы могут двигаться по кривым трех различных видов, наводит на мысль: не связаны ли три линии- эллипс, гипербола и парабола какими-то общими геометрическими свойствами? Действительно, все три линии можно охарактеризовать одним общим свойством: Все точки каждой линии равноудалены от некоторой точки и некоторой прямой.
2.Основные оптические свойства параболы.
Цели:
1. Познакомить учащихся с применением свойств параболы в жизни.
2. Доказать, что знание свойств параболы необходимо для будущего развития науки.
Квдратичная функция
Цель:
Показать необходимость применения оптических свойств параболы.
Адрес:
Учебник «Алгебра 9 класс», параграф 3, пункт 5., Дата и место рождения: Древняя Греция, Опыт работы:
1. Использование при изготовлении параболических отражателей для автомобильных фар и прожекторов. Выполнение роли отражателя.
2. Использование параболы, как траектории движения воды в фонтане.
3. Использование параболы для получения поверхности зеркала, называемого параболоидом вращения., Должность: Служащая., Дополнительная информация:, Парабола, как график квадратичной функции обладает некоторыми свойствами.
26 октября 2009г

Роберт Вуд 1868-1955

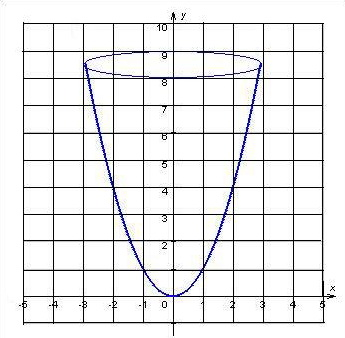
Траектория движения воды в фонтанах осуществляется в форме параболы.

Тема 3:
Парабола график квадратичной функции.
Цели:
1) Познакомить с понятием квадратичной функции
2) Рассмотреть способы получения графиков квадратичных функций
Квадратичная функция
-
Цель: Применение графика квадратичной функции в изучении математике и в природе.
-
Адрес: Алгебра 9 класс.
-
Дата и место рождения: Древняя Греция.
-
Опыт работы:
Графиком квадратичной функции является парабола. В зависимости от коэффициентов a , b , c парабола может менять своё направление, менять местоположение в прямоугольной системе координат, может расширять или сужать свои ветви.
В реальном мире многие предметы напоминают форму параболы, многие явления природы связаны с этой формой.
В математике уравнение параболы записывают в виде у=ах . Ось симметрии направлена по оси у. Вершина параболы находится в начале координат.
У=-х2
Рассмотрев график функции У= Х2 мы
видим, что график функции у=-х2 отображается
вниз относительно оси ОХ
Если а>1, то график выглядит следующим образом:, Е сли о<а<1,то график выглядит следующим образом:, Рассмотрев функцию у=а(х-
A ( m ; n )- вершина параболы
Хо = 2а ; Уо =У(Хо)
А(Хо ;Уо)-вершина параболы, Хо -ось симметрии
Тема 4:
Свойства квадратичной функции и её графика
Цель:
Квадратичная функция
Цель: решение квадратичных уравнений и неравенств, изучение других тем.
Адрес: учебник алгебры, 9 класс.
Дата и место рождения:, Опыт работы:, График имеет:
1) область определения
2) область значения
3) промежутки возрастания и убывания
4) нули, если: Д> 0, не имеет нулей если: Д< 0
5) промежутки знакопостоянства
6) ось симметрии
график функции симметричен относительно оси симметрии
Дополнительная информация

Нули функции
ах2+вх+с=0
-
D>0 – функция имеет два нуля
-
D=0 – функция имеет один нуль
-
D<0 – функция не имеет нулей
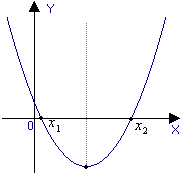
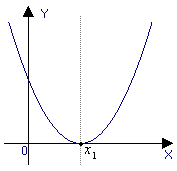
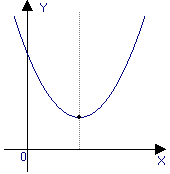
D >0 D =0 D <0
a >0 a >0 a >0
Промежутки убывания и возрастания
D >0 D >0
a<0
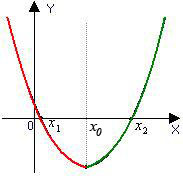
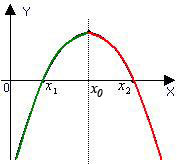
Далее каждая группа исследует квадратичную функцию и строить ее график., Дана функция у=
1. Найдите координаты вершины
параболы.
2. Найдите множество значений функции.
3. Найдите промежутки возрастания и убывания функции.
4. Найдите промежутки знакопостоянства функции.
5. Найдите нули функции.
6. Постройте график функции.
В конце урока учитель подводит итоги, делает вывод, что квдратичная функция играет важную роль в жизни человека.Учащиеся собрали необходимый материал по темам и подтвердили гипотезу. И в заключении ребята выражают свое отношение к уроку в форме сиквейна .
Понятие функции является центральным в курсе математики. От того, насколько полно и всесторонне школьник усвоит это понятие, зависит его дальнейшая адаптация в математической деятельности.
В школьном курсе математики учащиеся знакомятся с определением функции и той базы понятий, на котором оно основано, на протяжении всего периода обучения. У ребят должно быть сформировано с одной стороны ясное и четкое представление об этом понятии, а с другой стороны близкое к современному пониманию функции как некоторого отображения произвольных множеств.
В данном реферате сделана попытка, опираясь на основные школьные учебники, собрать материал по данной теме, систематизировать его для того, чтобы выделить важные моменты при формировании понятия функции и препятствовать формальному усвоению понятий, сопутствующих определению функции. Большую роль в достижении этой цели играют разработанные внеклассное мероприятие и урок, в которых учащиеся провели большую исследовательскую работу, познакомились с историей возникновения понятия, научились исследовать функцию и строить ее график.
Данная работа охватывает весь материал, связанный с понятием функции в школьном курсе и может быть использована при работе на уроках в обычных, профильных классах и на факультативных занятиях по математике.
Литература
[Электронный ресурс]//URL: https://inzhpro.ru/referat/tehnologiya-funktsiy/
1. Виленнкин. Н.Я. Рассказы о множествах, М.Наука,1969.
2. Пухначев Ю.В., Попов Ю.Т. Учись применять математику. Серия « Знание». – М., 1977.
3. В.Г. Коваленко. Дидактические игры на уроках математики: Книга для учителя. М., 1990г.
4. Энциклопедический словарь юного математика. М.,1998.
5. А.П. Рымкевич. Сборник задач по физике. М., 1995.
6. Р.Б. Райхмист. Графики функций, М., « Высшая школа», 1991.
7. Майер Р.А. Задачи по формированию функциональных понятий.
8. Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И. и др. Алгебра. Учебник для 7 класса общеобразовательных учреждений. М.: Просвещение, 1997.
9. Глейзер Г.И. История математики в школе 7-8 кл. М. Просвещение. 1982г.
10. Глейзер Г.И. История математики в школе 9-10 кл. М. Просвещение. 1983г.
11. Саранцев Г.И. Формирование математических понятий в средней школе // Матем. В школе. 1998. № 6. С.27.
