Основы теории подобия (метод обобщенных переменных)

метки: Подобие, Критерий, Применение, Техник, Величина, Уравнение, Подобный, Точка

Методы исследования технологических процессов

теоретическим, экспериментальным, подобия.

Теоретический метод

Однако многие процессы химической технологии так сложны, что удается лишь составить систему дифференциальных уравнений и установить условия однозначности. Решить эти уравнения известными в математике методами не представляется возможным.

Экспериментальный метод, Метод теории подобия, Теория подобия. Виды подобия

группы подобных явлений.

Подобными называются такие явления, для которых отношения сходственных и характеризующих их величин постоянны.

Различают следующие виды подобия: геометрическое; временное; физических величин; начальных и граничных условий.

Геометрическое подобие соблюдается при равенстве отношений всех сходственных линейных размеров натуры и модели. Например, при изучении движения жидкости в канале длиной L , диаметром D . В модели сходственные размеры равныl и d . Тогда

L/l =D/d= … = соnst= k_l (0)

константой геометрического подобия

Временное подобие предполагает, что сходственные частицы в геометрически подобных системах, двигаясь по геометрически подобным траекториям, проходят геометрически подобные пути за промежутки времени, отношение которых является константой подобия k _х , т.е.

(1)

На рис.1. изображен канал (натура) с размерами L и D и модель с размерами l и d . Некая частица в точке А (натура) находится в момент времени τ_А , в точке В — в момент времени τ_в . В геометрически подобной модели сходственная частица находится в подобной точке а в момент времени τ_а , в точке b— в момент времени τ _b .

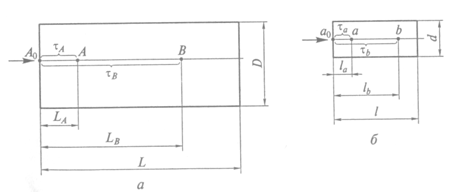
Рис. 1. Условия подобия в натуре (a) и в модели (б)

теория подобие переменная обобщенный

При соблюдении геометрического и временного подобия константа подобия скоростей k _υ определяется из соотношений

(2)

Подобие физических величин предполагает, что для двух любых сходственных точек натуры и модели, размещенных подобно в пространстве и во времени, соотношение физических величин (μ,ρи т.д.) является величиной постоянной:

Измерения геометрических величин в курсе геометрии 7-9 классов

... примем измеряемую геометрическую величину. Итак, в школьном курсе геометрии средней школы необходимо уметь измерять: длины отрезков, углы, площади. 4.1 Измерительные для измерения длин отрезков В первую ... такими методами геометрии как метод подобия, метод площадей, и используют другие методы: метод дополнительных метод вспомогательного треугольника, координатный метод, метод геометрических мест [16 ...

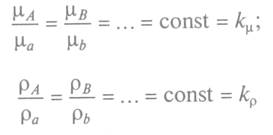(3)

и т.д.

Подобие начальных и граничных условий заключается в том, что для начальных и граничных условий должно соблюдаться геометрическое, временное и физическое подобие так же, как и для других сходственных точек натуры и модели.

Рассмотренные константы подобия постоянны для различных сходственных точек подобных систем, но могут изменяться в зависимости от соотношения размеров натуры и модели, т. е. если имеется другая модель, подобная натуре, константы подобия будут другими.

Если подобные величины выразить в относительных единицах, т.е. в виде отношений сходственных величин в пределах одной системы (натуры или модели), то получим инварианты подобия:

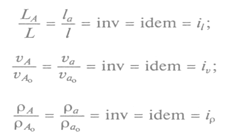
и т.д.

однородных

критериями подобия.

Критерии подобия безразмерны, их значения для разных точек системы могут быть различными, но для сходственных точек подобных систем они одинаковые и не зависят от относительных размеров натуры и модели.

Критерии подобия имеют физический смысл, являясь мерами соотношения между какими-то двумя эффектами, силами и т.п., оказывающими влияние на протекание данного процесса.

Критерии подобия могут быть получены для любого процесса, если известны уравнения, описывающие этот процесс.

Основные положения теории подобия (теоремы подобия)

Основные положения теории подобия заключены в теоремах подобия, которые лежат в основе практического применения теории подобия.

подобные явления характеризуются численно равными критериями подобия

Теорема была сформулирована Ньютоном. Она устанавливает, что единственным количественным условием подобия процессов является равенство критериев подобия натуры и модели.

Отсюда очевидно, что отношение критериев одной системы (натуры) к критериям другой подобной ей системы (модели) всегда равно 1. Например,

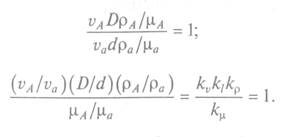
индикатора подобия

Следовательно, у подобных явлений индикаторы подобия равны 1.

Первая теорема подобия указывает, какие величины следует измерять при проведении опытов, результаты которых требуется обобщить: надо измерять те величины, которые входят в критерии подобия.

Вторая теорема подобия (теорема Бэкингем-Федермана): решение любого дифференциального уравнения, связывающего между собой переменные, влияющие на процесс, может быть представлено в виде зависимости между критериями К подобия. Такие уравнения называются уравнениями обобщенных переменных , или критериальными уравнениями , например

f(К _1, К₂ ,К₃ ,…) = 0, (5)

где К _1, К₂ , К₃ — критерии подобия.

Обычно критериальное уравнение записывается в виде зависимости определяемого критерия подобия от определяющих критериев подобия:

К ₁ =f(К₂ ,К₃ ,…)_, (6)

Например,

К ₁ =АК^m ₂ Кⁿ ₃ (7)

где А, т, п — эмпирические показатели.

Определяемым критерием является тот критерий, в который входит определяемая величина. Критерии, в которые входят величины, определяющие ход процесса ( v ,μ,ρ, d _э и т.д.), называются определяющими .

результаты эксперимента, проведенного на модели, можно представлять в виде критериальных уравнений.

явления подобны, если их определяющие критерии равны.

Следствием равенства определяющих критериев подобия является равенство и определяемых критериев для натуры и модели, поэтому полученная на модели в результате опытов критериальная зависимость будет справедлива для всех подобных процессов, в том числе и для протекающих в промышленной установке. При этом следует учитывать, что полученные уравнения надежно можно использовать только в тех интервалах изменения переменных, которые были использованы при проведении опытов.

Таким образом, для исследования технологических процессов методом подобия необходимо:

1. выбрать дифференциальное уравнение и условия однозначности, описывающие данный процесс; затем путем преобразования найти критерии подобия;

2. опытным путем с помощью моделей установить зависимость между критериями подобия; полученное обобщенное уравнение будет справедливым для всех подобных процессов в пределах изменения определяющих критериев подобия.

Преобразование дифференциальных уравнений методом теории подобия проводится в следующем порядке:

1. каждый из членов дифференциального уравнения умножается на соответствующие константы подобия к _τ , к_v , к_l ит.д.;

2. полученные коэффициенты перед членами уравнения для соблюдения тождественности приравниваются;

3. в полученных индикаторах подобия константы подобия заменяются соответствующими отношениями величин, и полученные комплексы являются критериями подобия.

В табл. 1 приведены основные критерии гидродинамического подобия, которые будут равны для сходственных точек натуры и модели, если они подобны.

Таблица 1

Критерий	Выражение критерия	Характеристика критериев	Единицы измерения входящих в критерии подобия величин
Кинематический (критерий Рейнольдса)	Rе= υl/ν= υlρ/μ	Характеризует меру соотношения сил инерции и сил трения	υ — скорость, м/с; l — определяющий размер, м; ρ — плотность, кг/м3 ; μ — динамическая вязкость, Па-с; ν — кинематическая вязкость, м2 /с; g — ускорение свободного падения, м/с2 ; р — давление, Па; τ-время, с
Гравитационный (критерий Фруда)	Fr = υ2 /gl	Характеризует меру соотношения сил инерции и сил тяжести
Гидравлического сопротивления (критерий Эйлера)	Еu =∆p/ ρ υ2	Характеризует меру соотношения сил гидростатического давления и сил инерции
Гомохронности	Но = υ τ/l	Характеризует неустановившееся движение жидкости

критериального

f (Rе, Но, Fr, Еu) = 0 (8)

обобщенным критериальным

Тогда

Еu = f (Rе, Но, Fr) или

Еu = AНо ^с Rе^т Fr^п , (9)

где А,c,т,п- эмпирические показатели.

В ряде случаев уравнение (19) дополняют геометрическим симплексом l / d :

Еu = AНо ^с Rе^т Fr^п (l / d )^b , (10)

где b- эмпирический показатель.

установившемся движении

Еu = ARе ^т Fr^п (l / d )^b . (11)

В случае, если скорость движения жидкости не определена, в расчеты вводят производные или модифицированные критерии подобия, составленные из основных критериев. В этих критериях подобия неизвестная величина υ заменяется другими величинами, которые сравнительно легко определяются экспериментально или аналитически.

Возьмем отношение критериев Rе и Fr:

(12)

Полученный безразмерный комплекс величин называется критерием Галилея. Если умножить этот критерий на отношение ( ρ ₁ — ρ ₂ )/ ρ ₂ , то получается новый критерий подобия — критерий Архимеда

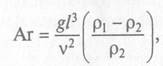(13)

где ρ ₁ , ρ ₂ — плотности жидкости в разных точках, кг/м³ .