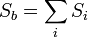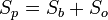(др.-греч. πυραμίς , род. п. πυραμίδος ) — многогранник, основание которого — многоугольник, а остальные грани — треугольники, имеющие общую вершину[1] . По числу углов основания различают пирамиды треугольные, четырёхугольные и т. д. Пирамида является частным случаем конуса.
1. История развития геометрии пирамиды
Начало геометрии пирамиды было положено в Древнем Египте и Вавилоне, однако активное развитие получило в Древней Греции. Первый, кто установил, чему равен объем пирамиды, был Демокрит [2] , а доказал Евдокс Книдский. Древнегреческий математик Евклид систематизировал знания о пирамиде в XII томе своих «Начал», а также вывел первое определение пирамиды: телесная фигура, ограниченная плоскостями, которые от одной плоскости сходятся в одной точке .
2. Элементы пирамиды
- апофема — высота боковой грани правильной пирамиды, проведенная из ее вершины [3] ;
- боковые грани — треугольники, сходящиеся в вершине пирамиды;
- боковые ребра — общие стороны боковых граней;
- вершина пирамиды — точка, соединяющая боковые рёбра и не лежащая в плоскости основания;
- высота — отрезок перпендикуляра, проведённого через вершину пирамиды к плоскости её основания (концами этого отрезка являются вершина пирамиды и основание перпендикуляра);
- диагональное сечение пирамиды — сечение пирамиды, проходящее через вершину и диагональ основания;
- основание — многоугольник, которому не принадлежит вершина пирамиды.
3. Углы пирамиды , 4. Развёртка пирамиды
Разверткой называется плоская фигура, полученная при совмещении поверхности геометрического тела с одной плоскостью (без наложения граней или иных элементов поверхности друг на друга).
Приступая к изучению развертки поверхности, последнюю целесообразно рассматривать как гибкую, нерастяжимую пленку. Некоторые из представленных таким образом поверхностей можно путем изгибания совместить с плоскостью. При этом, если отсек поверхности может быть совмещен с плоскостью без разрывов и склеивания, то такую поверхность называют развертывающейся, а полученную плоскую фигуру – ее разверткой.
Египетские пирамиды
... вершины их были покрыты медными плитами, сверкавшими на солнце (известняковую обшивку сохранила только пирамида Хефрона, покрытие других пирамид арабы использовали при строительстве ... над скрытым под поверхностью захоронением. Надстройка сооружалась ... пирамида Хафра[2](греческое название Хефрен), а затем пирамида Менкаура [1](греч.Микерин). Высота пирамиды Хеопса - 146.6 метров, длина стороны основания ...
5. Свойства пирамиды
- Все диагонали пирамиды принадлежат её граням.
Если все боковые ребра равны , то:
- около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр;
- боковые ребра образуют с плоскостью основания равные углы.
- также верно и обратное, то есть если боковые ребра образуют с плоскостью основания равные углы или если около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр, то все боковые ребра пирамиды равны.
Если боковые грани наклонены к плоскости основания под одним углом , то:
- в основание пирамиды можно вписать окружность, причём вершина пирамиды проецируется в её центр;
- высоты боковых граней равны;
- площадь боковой поверхности равна половине произведения периметра основания на высоту боковой грани.
6. Теоремы, связывающие пирамиду с другими геометрическими телами
6.1. Сфера
- около пирамиды можно описать сферу тогда, когда в основании пирамиды лежит вписанный многоугольник (необходимое и достаточное условие).[4] Центром сферы будет точка пересечения плоскостей, проходящих через середины рёбер пирамиды перпендикулярно им. Из этой теоремы следует, что как около любой треугольной, так и около любой правильной пирамиды можно описать сферу;
- в пирамиду можно вписать сферу тогда, когда биссекторные плоскости внутренних двугранных углов пирамиды пересекаются в одной точке (необходимое и достаточное условие).
Эта точка будет центром сферы.
6.2. Конус
- Конус называется вписанным в пирамиду, если вершины их совпадают, а его основание вписано в основание пирамиды. Причём вписать конус в пирамиду можно только тогда, когда апофемы пирамиды равны между собой (необходимое и достаточное условие);[5]
- Конус называется описанным около пирамиды, когда их вершины совпадают, а его основание описано около основания пирамиды. Причём описать конус около пирамиды можно только тогда, когда все боковые ребра пирамиды равны между собой (необходимое и достаточное условие);
- Высоты у таких конусов и пирамид равны между собой.
6.3. Цилиндр
- Цилиндр называется вписанным в пирамиду, если одно его основание совпадает с окружностью вписанной в сечение пирамиды плоскостью, параллельной основанию, а другое основание принадлежит основанию пирамиды.
- Цилиндр называется описанным около пирамиды, если вершина пирамиды принадлежит его одному основанию, а другое его основание описано около основания цилиндра. Причём описать цилиндр около пирамиды можно только тогда, когда в основании пирамиды — вписанный многоугольник (необходимое и достаточное условие).
16 стр., 7639 слов
Основание Самары (население города и его окрестностей)
... "река". Таким образом, Самар, или в более позднем варианте Самара, означает "река знойных степей" или просто "степная река". II. Основание Самары 1. Крепость Самара Официально датой основания Самары считается 1586 год, ... утес, носящий его имя, существует множество легенд о сокровищах Стеньки, якобы спрятанных около этого утеса. 2. Уездный город В 1688 году указом Петра I самарской ...
7. Формулы, связанные с пирамидой
- Объём пирамиды может быть вычислен по формуле:
-
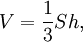
- где — площадь основания и — высота;
- Боковая поверхность — это сумма площадей боковых граней:
- Полная поверхность — это сумма боковой поверхности и площади основания:
- Для нахождения боковой поверхности в правильной пирамиде можно использовать формулы:
-
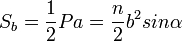
- где a — апофема боковой грани, — периметр основания, — число сторон основания, — боковое ребро, α — плоский угол при вершине пирамиды.
8. Особые случаи пирамиды
8.1. Правильная пирамида
Пирамида называется правильной, если основанием её является правильный многоугольник, а вершина проецируется в центр основания. Тогда она обладает такими свойствами:
- площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.
8.2. Прямоугольная пирамида
Пирамида называется прямоугольной, если одно из боковых рёбер пирамиды перпендикулярно основанию. В данном случае, это ребро и является высотой пирамиды.
8.3. Усечённая пирамида
Усечённой пирамидой называется многогранник, заключённый между основанием пирамиды и секущей плоскостью, параллельной её основанию.
9. Связанные определения
Тетраэдром называется треугольная пирамида. В тетраэдре любая из граней может быть принята за основание пирамиды. Кроме того, существует большое различие в понятиях правильная треугольная пирамида и правильный тетраэдр.
10. Интересные факты
- Формула для расчёта объёма усечённой пирамиды была выведена раньше, чем для полной.
Примечания
Литература
[Электронный ресурс]//URL: https://inzhpro.ru/referat/piramida-v-prirode-i-tehnike/
- Александров А.Д. Вернер А.Л. Учебник для 10-11 классов общеобразовательных учреждений. — 2-е. — Просвещение, 2003. — 271 с. — ISBN 5-09-010773-4
- А. Ю. Калинин, Д. А. Терешин Стереометрия. 11 класс. — Физматкнига, 2005. — ISBN 5-89155-134-9
- А. В. Погорелов Геометрия: Учебник для 10-11 классов общеобразовательных учреждений. — Просвещение, 2008. — ISBN 978-5-09-019708-3
Данный реферат составлен на основе .
Проектирование оснований фундаментов
... коэффициенты. При проектировании столбчатых фундаментов расчет предполагает фундамент квадратной формы в плане, рассчитывается ориентировочный размер подошвы фундамента. Проектирование оснований и фундаментов мелкого заложения ... послойного суммирования (СНиП 2.02.01-83* «Основания зданий и сооружений»). 2. Определение осадки столбчатого фундамента мелкого заложения методом эквивалентного слоя (метод ...