Одной из основных задач химической технологии является создание новых высокоэффективных процессов и совершенствование уже действующих. Ее решение возможно только с помощью разработки и использования систем автоматического проектирования и оптимизации химико-технологических процессов. Развитие систем автоматизированного проектирования обусловлено широким внедрением вычислительной техники и прикладного математического обеспечения. В основе таких систем лежит метод математического моделирования — изучение свойств объекта на математической модели.
Целью математического моделирования является определение оптимальных условий протекания процесса, управление им на основе математической модели и перенос результатов на объект.
Математической моделью называется приближенное описание какого-либо явления или процесса, выраженное с помощью математической символики.
Математическое моделирование включает три взаимосвязанных этапа:
- составление математического описания изучаемого объекта;
- выбор метода решения системы уравнений математического описания и реализация его в форме моделирующей программы; установление соответствия (адекватности) модели объекту.
На этапе составления математического описания предварительно выделяют основные явления и элементы в объекте и затем устанавливают связи между ними. Далее, для каждого выделенного элемента и явления записывают уравнение (или систему уравнений), отражающее его функционирование. Кроме того, в математическое описание включают уравнения связи между различными выделенными явлениями. В зависимости от процесса математическое описание может быть представлено в виде системы алгебраических, дифференциальных, интегральных уравнений.
Этап выбора метода решения и разработки моделирующей программы подразумевает выбор наиболее эффективного метода решения из имеющихся (под эффективностью имеются в виду быстрота получения и точность решения) и реализацию его сначала в форме алгоритма решения, а затем — в форме программы, пригодной для расчета на ЭВМ. Построенная на основе физических представлений модель должна верно качественно и количественно описывать свойства моделируемого процесса, т.е. она должна быть адекватна моделируемому процессу. Для проверки адекватности математической модели реальному процессу нужно сравнить результаты измерений на объекте в ходе процесса с результатами предсказания модели.
Математическая модель
... -модели называется моделированием.» (с. 6) «Под математическим моделированием будем понимать процесс установления соответствия данному реальному объекту некоторого математического объекта, называемого математической моделью, и исследование этой модели, позволяющее получать характеристики рассматриваемого реального объекта. Вид математической модели ...
В данном технологическом процессе производится разбавление щелочи HaOH водой до требуемой концентрации. Затем разбавленная щелочь нагревается до необходимой температуры. Данный технологический процесс является небольшим фрагментом производства гипохлорита натрия, который в дальнейшем применяется для отбеливания целлюлозы.
Схема технологического процесса имеет следующий вид:
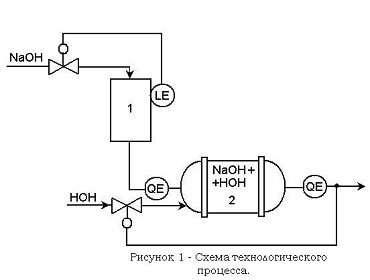
Данный технологический процесс можно разбить на две модели систем автоматического регулирования:
Модель системы автоматического регулирования уровня NaOH в баке №1.
Модель смесителя №2 (модель идеального перемешивания).
Модель идеального смешения
Опишем аппарат идеального смешения. Представим себе аппарат с мешалкой, через который проходит поток (рисунок 1).
Мощность мешалки такова, что поступающая жидкость мгновенно перемешивается с массой, уже находящейся в аппарате. Таким образом, все, что попадает в аппарат идеального смешения, мгновенно распределяется по всему его объему.
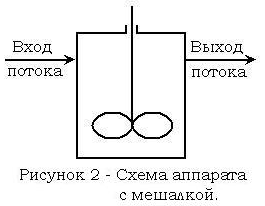
Перечислим важнейшие следствия из этого определения: 1. Концентрации всех веществ равномерно распределены по объему аппарата. В любой паре точек в аппарате любая из этих величин имеет одно и то же значение.
На выход поток выносит ту жидкость, которая находится в аппарате. Поэтому на выходе из аппарата идеального смешения концентрация та же, что в объеме.
На входе в аппарат концентрация претерпевает скачок: исходные значения параметров потока, мгновенно смешивающегося с содержимым аппарата, соответственно мгновенно изменяются до тех значений, которые характеризуют режим в аппарате и на выходе из него.
Время пребывания жидкости в аппарате идеального смешения распределено неравномерно. Действительно, распределяя по объему вошедшую порцию жидкости, наша идеальная мешалка пошлет к выходу некоторые частицы из этой порции и они сразу уйдут из аппарата, в то время, как другие, попавшие в иные части аппарата, могут задерживаться в нем весьма надолго.
Используя то обстоятельство, что концентрация во всех точках аппарата одинакова, можно очень просто записать обобщенное уравнение материального баланса:
2. Приход вещества — расход вещества = накопление вещества
Таким образом, уравнение материального баланса для нашей модели идеального смешивания будет иметь следующий вид:
(1.1)
где Q1 и Q2 — расход смешиваемой (в нашем случае NaOH) и смешивающей (H2O) жидкостей соответственно. C1 и С2 — концентрация смешиваемой и смешивающей жидкостей соответственно. Q и C — расход и концентрация смешанной (вышедшей из аппарата) жидкости.
Перепишем уравнение (1.1) в следующий вид:
(1.2)
Уравнение (1.2) почленно поделим на Q, тогда получим:
(1.3)
В уравнении (1.3) 
и 
, где Т — постоянная времени нашего объекта, а k — коэффициент усиления.
Подставив Т и k в уравнение (1.3) получим уравнение следующего вида:
(1.4)
Теперь уравнение (1.4) поделим почленно на постоянную времени Т, в результате чего получим:
(1.5)
Полученное уравнение (1.5) и будет описывать нашу модель идеального смешения. В соответствии с ним реализуем модель аппарата идеального смешения в пакете Simulink среды MatLab 6.5. При моделировании необходимо учесть, что величины Q1 и С1 (расход и концентрация NaOH) являются постоянными. Прежде чем моделировать необходимо ввести исходные данные для моделирования.
Таблица 1.1 — Исходные данные для моделирования аппарата идеального смешения.
|
С1(NaOH), % |
Q1(NaOH), м3/сек. |
C2(HOH), % |
Q2(HOH), м3/сек. |
V(смесителя), м3 |
|
56,65 |
0,0006 |
10 |
0,0001 |
0,000785 |
В MatLab-е представим нашу модель в следующем виде:
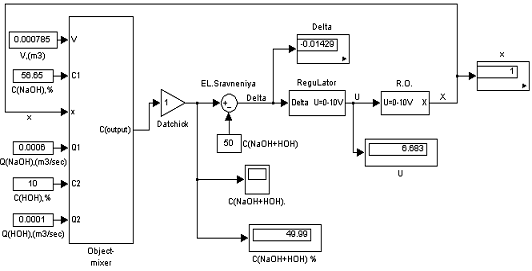
Рисунок 3 — Схема модели идеального смешения в среде MatLab.
Схема состоит из трех основных подсистем: объекта регулирования (Object-mixer), регулятора (ReguLator) и регулирующего органа (R.O.).
В объекте регулирования реализуется дифференциальное уравнение (1.5) посредством блоков суммирования, деления, умножения и интегрирования:
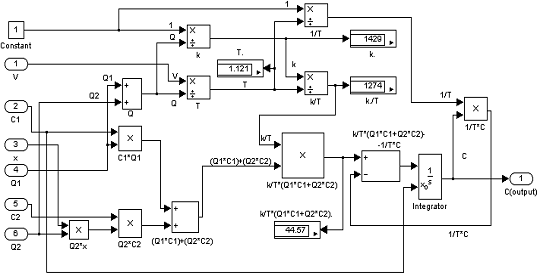
Рисунок 4 — Схема подсистемы (Object-mixer)
С помощью подсистемы, реализирующей регулятор, на вход которого поступает сигнал рассогласования (Delta) с элемента сравнения (EL.Sravneniya) осуществляется формирование управляющего сигнала (U) в диапазоне от 0 до 10 В на регулирующий орган (R.O.).
Регулирующий орган, в свою очередь, формирует сигнал (Х), который управляет ходом штока.
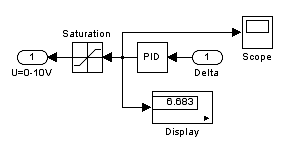
Рисунок 5 — Схема подсистемы регулятора (ReguLator).
Звено Saturation в подсистеме регулятора служит для того, чтобы сигнал со звена PID ни в коем случае не мог превысить 0ч10 В (0ч10 В — стандартный выход для электрического регулятора).
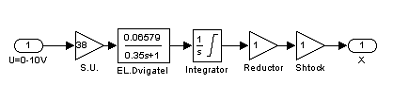
Рисунок 6 — Схема подсистемы регулирующего органа (R.O.)
Звено S.U. в схеме R.O. необходимо для того, чтобы согласовать управляющий сигнал с регулятора в управляющий сигнал для двигателя, т.е. S.U. в данном случае выполняет роль усилителя.
На выходе электродвигателя (EL.Dvigatel) частота вращения вала, пропорциональная напряжению на входе (US.U.= 0ч380 В).
В результате реализации схемы получился график следующего вида:
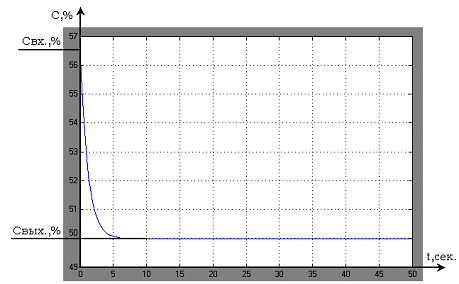
Рисунок 7 — График процесса регулирования процесса идеального смешения.
В данной модели бака необходимо поддерживать постоянный уровень для того, чтобы расход поступающего в смеситель NaOH был постоянный, что, в свою, очередь требуется для того, чтобы можно было разбавлять NaOH водой в смесителе. Т.е. концентрация NaOH регулируется расходом воды, поступающей в смеситель.
Для того, чтобы смоделировать наш бак, необходимо ввести исходные данные и математически описать резервуар.
математический моделирование разбавление щелочь
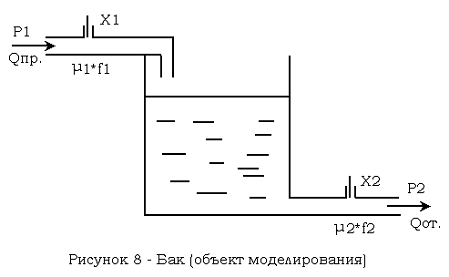
где Q — расход (пр — приток, от. — отток) μ — коэффициент истечения крана f — поперечное сечение трубы Х — управляющее воздействие
Вещество — NaOH
Удельный вес NaOH γ = 10388 Н/м3
Диаметр бака — 2 м.
Высота бака — 4,5 м.
Диаметр подходящей трубы d1=0.09 м
Диаметр отходящей трубы d2 = 0.1 м
Коэффициент истечения крана на входе μ1=0,3
Коэффициент истечения крана на выходе μ2=0,2
Давление на входе в бак Р1= 65900 кПа
Давление на выходе в бак Р2= 6500 кПа
Уравнение материального баланса для нашей модели будет иметь вид:
Qпр=Qот (2.1)
Перепишем уравнение баланса в следующем виде:
, (2.2)
где Нн — уровень жидкости в рассматриваемом баке
Определим численные значения уравнения (2.2):
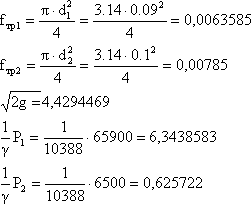(2.3)
Подставим численные значения в уравнение (2.2) и определим величину НН:
(2.4)
Из уравнения (2.4) определим величину НН, реализовав уравнение (2.4) в MatLab-е:
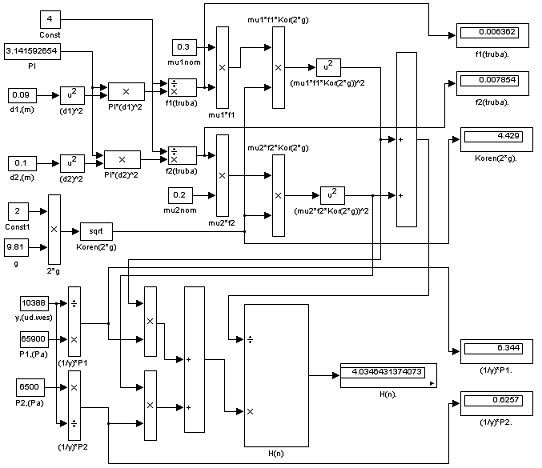
Расход жидкости Qот при НН= 4,0346431 м:
(2.5)
Вычислим высоту столба жидкости над дном бака ZH, которая будет равна разности между значением НН и высотой столба жидкости НР2, эквивалентного давлению напора Р2Н на линии:
(2.6)
(2.7)
Площадь поперечного сечения бака:
(2.8)
Зная площадь бака, можно найти объем жидкости в баке:
(2.9)
Постоянная времени Та:
(2.10)
Определим коэффициенты самовыравнивания на притоке и оттоке, для чего перепишем уравнения для притока и оттока следующим образом:
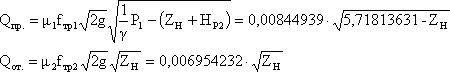(2.11)
Коэффициенты самовыравнивания будут равны:
(2.12)
Соответственно коэффициент самовыравнивания объекта равен:
(2.13)
Передаточная функция нашего объекта будет иметь вид:
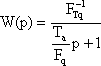(2.14)
где 
— коэффициент усиления, а 
— постоянная времени объекта. Подставим значения К и Т в уравнение (2.14):
(2.15)
Выражение (2.15) и будет являться передаточной функцией бака.
Реализуем нашу модель в среде MatLab. Она будет выглядеть следующим образом:
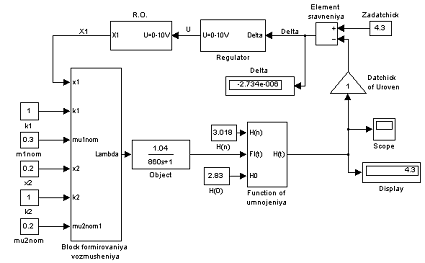
Рисунок 9 — Модель резервуара
Модель резервуара состоит из четырех подсистем (блока формирования возмущений, функции умножения, регулятора и регулирующего органа) и непосредственно передаточной функции объекта (резервуара с NaOH).
Ниже приведены схемы подсистем.
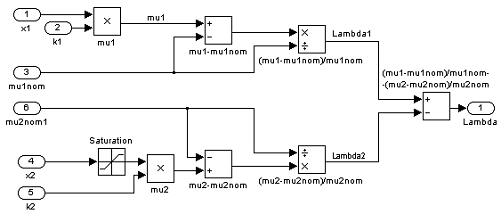
Рисунок 10 — Подсистема блока формирования возмущений.
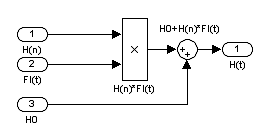
Рисунок 11 — Подсистема — функция умножения.
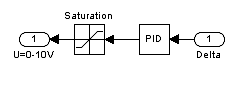
Рисунок 12 — Подсистема регулятора.
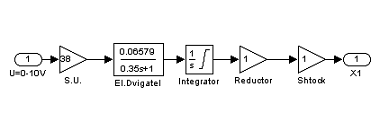
Рисунок 13 — Подсистема регулирующего органа.
В результате получился следующий график процесса регулирования:
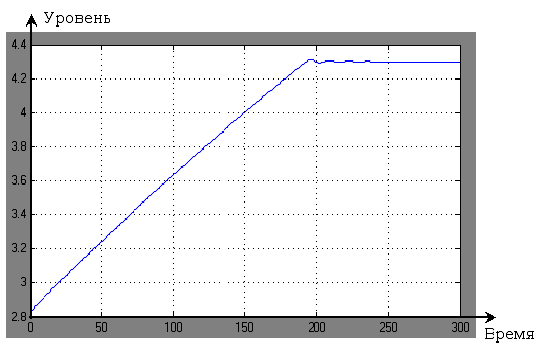
Рисунок 14 — Процесс регулирования бака с NaOH.
В данном курсовом проекте были рассмотрены и смоделированы с помощью пакета визуального программирования SIMULINK (пакет Matlab 6.5) следующие модели систем регулирования объектов химической технологии: модель идеального смешения, модель регулирования уровня NaOH в резервуаре.
Представлены графики зависимости регулируемых величин в зависимости от времени.
1. Луценко В.А., Финякин Л.Н. Аналоговые вычислительные машины в химии и химической технологии. — М.: Химия, 1979 — 248 с.
. Машины и аппараты химических производств. Под ред. И.И. Чернобыльского. — М.: Машиностроение, 1974. — 456 с.
. Закгейм А.Ю. Введение в моделирование химико-технологических процессов. — 2 — е изд., перераб. и доп. — М.: Химия, 1982. — (серия «Химическая кибернетика») 288 с., ил.
. Лурье Ю.Ю Справочник по аналитической химии. 5-е изд., перераб. и доп. — М.: Химия. 1979. — 480
