Системы стабилизации и ориентации

метки: Система, Матрица, Стабилизация, Дискретный, Непрерывный, Устойчивость, Пример, Коэффициент

? ????????? ????? ? ?????????????? ? ???????? ????????? ??????????? ??????? ????? ?????? ??????????????? ????????????? (???), ??????? ???????????? ??????? ????????????? ???????????????? ?????????. ??????? ?????? ??????????????? ????????????? ????????? ?? ???? ?????? ??????? ?????????? ? ???????? ????? ?? ??????? ?????????. ?? ?? ?????? ? ?????????? ???????? ????? ?????, ??? ?????? ??????????????? ??????????, ?????????????????? ??????? ??????????? ??????????, ?????????? ???????????????? ? ??????????????-?????????????? ??????????, ?????? ??????????????????? ?????????????? ?????? ? ?? ?????????????? ???????????, ? ????? ????? ??? ????????? ???????????? ??????????. ??????? ? ?????????? ?????? ????????????? ?????????? ?? ????? ?????????? ??????? ? ????????? ??????????, ??????? ?????????????? ?????????? ?? ?????? ????? ??????? ?????????? ? ??????? ????????, ???????????, ?????????????? ? ?????????????? ???????, ?? ? ????? ????????? ????????????? ??????????? ???????. ? ????? ????????? ????????????? ???????? ????????????? ??????? ?????? ??????????????? ????????????? ??????? ??????????? ? ???????? ???????? ????????? ???????? ???????, ???????? ? ????????? ?????? ?? ?????????????? ?????? ?????????? ??????????? ?????????.

????????? ?????????? ????????? ????? ? ???????????? ??????? ???????????? ?????????? ??????????????? ????????, ????????????? ??? ???????? ???????? ? ?????? ??????????????? ?????????????. ??????? ??? ?????????? ??????? ????? ?????? ??????????????? ????????????? ????? ????? ???????? ????????, ??????????? ??? ?????????? ?????????????? ??????. ??? ????????? ??????????? ?????????? ?????? ????????? ? ?????????? ????? ? ??????? ???????????? ???????; ??????? ??????????-??????? ????????? ?????????????? (? ??????? ? ??????????????? ?????????) ? ??.

1 ????? ??????????

1.1 ????????? ?????????? ?????? ??????????? ???????

При проектировании непрерывных, дискретно-непрерывных и дискретных САР необходимо располагать математической моделью элемента (объекта).

При высоких порядках моделей удобно пользоваться уравнениями, составленными во временной области и записанными в векторно-матричной форме. Рассмотрим одну из наиболее часто встречающихся форм представления многоконтурных стационарных линейных элементов (объектов).

При этом будем считать, что в линейный объект регулирования после ряда преобразований входят лишь две матрицы: ? и ?. Тогда эту форму представления стационарного объекта можно записать в виде векторно-матричного уравнения

Современные формы регулирования оценочной деятельности

... оценочной деятельности; рассмотреть правовое регулирование оценочной деятельности; рассмотреть подходы оценки; провести анализ регулирования оценочной деятельности в Российской Федерации и зарубежных странах изучить проблематику регулирования оценочной деятельности в Российской Федерации. Объект- вопросы регулирования оценочной деятельности. Предмет-анализ регулирования оценочной деятельности ...

, (1.1)

где ? и u — ??????? ???????????? ( n ? 1 ) и (m ? 1 ); ? ? ? — ??????? ??????????? (n? n ) и (n? m ).

С целью использования одинаковой формы описания объектов непрерывных, дискретно-непрерывных и дискретных САР пользуются теорией спектрального разложения матриц, которая с помощью специально созданных алгоритмов позволяет получать единые математические модели в дискретной форме. К основному преимуществу такого подхода следует отнести возможность представления моделей с использованием матриц до 50-80-го порядков, без существенного понижения точности спектрального разложения матриц.

?????????? ?????????, ? ??????? ??????? ???????????? ?????????? ?????? ??????????? ????????, ??????????? ??????? ????????-????????? ?????????? (1.1).

????????????? ??????? ????? ????????? ??? ????????? ???????? y(t ₀ ) ????? ???

(1.2)

? ??????? ??????? t=?T ₀ ? t=(?+1)? ₀ ????????? ??????? у _?+1 связано с предыдущим состоянием ? _к ????????????

(1.3)

???

• ?????????? ??????? ??????? ?????????.

?????????????? ??????????? ??? ?????????? ?????????? ??????? ????? ????????? ? ????? ?????? ???????????????.

Самая простая дискретная модель может быть получена, если положить, что внутри интервала квантования сигнала, ? (t) экстраполируется по одной точкеступеньки со значениями ? _к , ?.?. ????? ???????? ??????? ????????????? ???????? ??????? ?₀ . В этом случае соотношение (1.3) можно представить в виде

? _к+1 =?? _к +F? _к . (1.4)

????? F=(? — I)? ^-1 ? — ??????? ?????????????, ?????????????? ???????? ???????? ?? ?????? ?????????? ??????.

1.2 ???????????? ??????? ??????????? ? ?????????? ??????

Под передаточной функцией стационарных элементов понимают отношение изображения выходной величины к изображению функции входной величины, полученные при нулевых начальных условиях. Для многоконтурных стационарных элементов возможно получение матрицы передаточных функций на основе модели системы во временной области в векторно-матричной форме (1.1).

Применяя преобразование Лапласа, получим:

IX(s)=AX(s)+BU(s), (1.5)

где I — единичная матрица. Путем несложных преобразований найдем:

X(s)=(Is – A) ^-1 BU(s).

(1.6)

Таким образом, матрицу передаточных функций в общем виде можно записать так:

M _U =X(s)/U(s)=(Is – A)^-1 B (1.7)

1.3 Частотные характеристики непрерывных и

дискретных систем

????????? ?????????????? ???????? ??????????? ?????? ????????? ?? ???????????? ??????? ????? ??????????? ? ??? s=jw и выделения действительной мнимой частей, т.е.

W ₀ (jw)=U ₀ (w)+jV ₀ (w), (1.8)

Система непрерывного профессионального образования

... систему образования. Сегодня знания обновляются на 15% ежегодно. Таким образом, общегосударственной задачей является создание системы непрерывного профессионального образования в России, чтобы восполнить дефицит высококвалифицированной рабочей силы и этим определяется актуальность данной темы. ...

г?? U ₀ (w) ? V ₀ (w) — соответственно действительная и мнимая частотные характеристики.

????????? ?????????? (1.8), ? ?????????? ??????? ????????? ?????? ??????????-??????? ????????? ?????????????? W ₀ (jw). Если перейти к полярной системе координат, то выражение (1.8) можно переписать в виде

(1.9)

где

и q ₀ (w) — соответственно амплитудная и фазовая частотные характеристики.

Из выражений (1.8) и (1.9) можно найти формулы для вычисления амплитудной и фазовой частотных характеристик:

(1.10)

Частотные характеристики линейных дискретных систем находятся путем подстановки в передаточные функции

?? ???????? ??????????? ? ??????? ????????? ?????????????? ?????? ?? ??????????????????? ??????. ????? ??? w ????????? ? ??????????????? ????????, ??? ????????? ??????? ? 10 ??? ?????????? ???????, ?????????

??????????? ? ????????? ? ???? q ? ????????.

1.4 ?????? ???????????? ??????????? ? ?????????? ??????

Системы стабилизации должны обеспечивать устойчивость и заданную точность регулирования отклонений углов и координат центра масс ЛА от программных значений. При этом могут налагаться ограничения на значения отдельных параметров системы (управляющие воздействия или производные управляющих воздействий).

Отклонения углов и угловых скоростей могут ограничиваться для определенных возмущающих воздействий.

?????? ??????????? ???????????? ???????? ???????????? ??? ??????? ?????? ???????????? ??. ???????? ??????? ?? ???????? ????????? ??????? ????????? ??????????, ???? ?? ???? ????????? ??? ???????? ????????? ???????? ? ??????????? ?????????? ??? ????????? ?? ????????? ???????? ??????????? — техническая устойчивость. Если система содержит существенные нелинейности, то для устойчивости при заданных начальных условиях и действующих возмущений необходимо чтобы при начальной амплитуде периодической составляющей, превышающей её установившееся значение с течением времени эта амплитуда стремилась к своему установившемуся значению, а параметры установившегося движения не превышали заданных ограничений.

Для анализа устойчивости линейной или линеаризованной системы используется понятие асимптотической устойчивости, при этом обычно Используется стационарные математические модели, полученные с использованием метода замороженных коэффициентов. Система является асимптотически устойчивой, если:

• ???? ??????????? ?????? — ????? ??????????????????? ???????? ????? ? ????? ?????????????;
• ?для дискретных систем — корни характеристического полинома лежат внутри окружности единичного радиуса.

Устойчивость непрерывных систем может исследоваться с помощью первого метода Ляпунова, а также алгебраических критериев (Гурвица, Рауса и Льенара-Шепара).

Для дискретных систем используется критерий Кларка и Шур-Кона. Основным недостатком применения данных критериев следует считать невозможность получения при этом оценок качества и точности. Пользуясь ими для систем высокой размерности, проектировщик не может дать рекомендаций по выбору параметров, не только обеспечивающих запасы устойчивости, но и удовлетворяющих требованиям к качеству и точности процессов регулирования. Следует отметить, что на устойчивость дискретных нелинейных систем большое влияние оказывает выбор такта квантования.

????????? ???????? ???????????? ???????????? ????????????? ???????????? ??????? ??? ???????? ??????? ????????????? ? ??????????? ??? ?? ?????? ????????????? ? ?????????????. ????? ???????? ???????????? ?? ???????? ?????????? ????????? ?????????, ?????????-????????? ? D-?????????? ????????. ??? ???????? ????????? ? ??????? ??? ???????????, ??? ? ?????????? ??????. ?????? ? ?????? ?????? ??? ?????????? ?? ??????? s-??????????????, ?? ?????? — z-??????????????. ??????? s=jw или z=e ^{j w T 0} , строятся частотные характеристики, по которым определяются устойчивости систем регулирования по фазам и модулям и с помощью специальных номограмм оценивают показатели качества и характеристики точности. Большим преимуществом частотных критериев устойчивости является возможность их распространение и на многие типы нелинейных систем.

При проектировании систем стабилизации ЛА чаще всего используются алгебраические и частотные критерии, реже корневые.

1.4.1 Корневые критерии заключаются в вычислении корней

характеристического полинома замкнутой системы.

1.4.2 Алгебраические критерии устойчивости не требуют выполнения вычислительной процедуры определения корней характеристического уравнения и при относительно невысоких порядках дифференциальных уравнений (до 15-го) позволяют находить условия устойчивости автономных замкнутых систем.

?(s)=a _n sⁿ + a_n-1 s^n-1 + a_n-2 s^n-2 +…+a₀ . (1.11)

???????? ???????. Корни характеристического уравнения (1.11) n-го порядка будут иметь отрицательные действительные части, если составленный из его коэффициентов а _i > 0 определитель

(1.12)

? ??? ??? ???????????? ??????

(1.13)

положительны.

???????? ?????. Зная коэффициенты характеристического уравнения, составляют таблицу Рауса(табл. 1.1).

Для того чтобы замкнутая система была устойчива асимптотически, необходимо и достаточно, чтобы все коэффициенты Рауса первого столбца таблицы при а _i >0 были положительны, т.е. с_{i ,1} >0 (i=1,2,…).

Для вычисления элементов табл. 1.1 можно использовать следующие рекуррентные формулы:

для первой строки таблицы

(1.14)

для второй строки таблицы

(1.15)

??? ????????? ?????

(1.16)

Таблица 1.1

?????? ?????	?????? ????????
1	2	3	…….	I
???????????? ? ??????? ?????????
а 0	а 2	а 4	…….
???????????? ? ????????? ?????????
а 1	а 3	а 5	……..
1	С 11	С 12	С 13	……..	С 1 i
2	? 21	? 22	? 23	……..	C 2 i
….	……	…..	…..	…….	……
к	С ?1	С ?2	С ?3	……..	С i к

???????? ???-????. Данный критерий позволяет анализировать устойчивость дискретных и дискретно-непрерывных систем по характеристическому полиному замкнутой системы, записанному в форме z-преобразования. Для уравнения n-го ??????? ?????

A(z)=a _n zⁿ + a_{n -1} z^{n -1} + a_{n -2} z^{n -2} +…+a₀ . (1.17)

По уравнению запишем коэффициенты в виде определителя

(1.18)

где k=1,2,…,n; a ^* — сопряженные значения тех же коэффициентов.

????? ??????????????????? ????????? (1.18) ????? ?????????? ?????? ????????? ??????????, ???? ???????????? ????????? (1.17) ????????????? ???? ????????????? ???-????, ???????? D _k < 0 — ??? ???????? k ? D_k > 0 для четных k. В этом случае система будет устойчива

???????? ??????. Представляет собой совокупность 3-х необходимых условий, и лишь выполнение всех этих условий является условием устойчивости системы:

1. А(1) > 0

2. (-1)?(-1) > 0

3. Необходимо вычислить определители матриц D ⁺ и D^— , ? ????? ?? ?????????? ???????. ?????????? ??????? ?????????? ?? ???????? ????????????? ??????????? ????? ? ????????. ?????????? ??????? ???????????? ??????? ?? ??????? ???????.

D ⁺ =C_{n -1} +B_{n -1} ; D^— =C_{n -1} -B_{n -1} ; (1.19)

(1.20)

??????? ?????????, ???? ???????????? ?????? D⁺ и D^— , ? ????? ???? ?? ?????????? ?????? ????????????. ??????? ?? ?????????, ???? ?? ??????????? ???? ?? ???? ?? ??????? ???????????? ??????.

1.5 Синтез цифровых систем управления по желаемым частотным характеристикам разомкнутой системы

Одно из направлений развития алгоритмических методов синтеза базируется на использовании частотных методов исследования. Процедура машинного синтеза формируется при этом как задача аппроксимации оптимальной в определенном смысле частотной характеристики разомкнутой системы (так называемой желаемой характеристики) исходной характеристикой.

Приближение исходной характеристики к желаемой достигается применением законов управления (корректирующих устройств) минимальной сложности и осуществляется в выбранных характерных точках частот по критерию минимума средних квадратов. При этом под корректирующим устройством минимальной сложности понимается устройство, имеющее наименьшую размерность.

????? ???????? ???? ??????????? ??????? ???????? ? ??????, ??????????????? ????????? ?????????????? l_? , к=1,2,…,m

W(jl _к )=U_? +jV_к . (1.21)

Для некотор?х значений параметров наперед выбранного закона управления D(z) ????? ?????????? ???? ????????????????? ??????? W _?? (jl_? ) ?? ???? ?? ????????? ??????? l_? :

W _ск (jl _к )=W ₀ (jl _? )D(jl _? )=Re _к +jIm _? , (1.22)

где W ₀ (jl_к ) — ????????? ?????????????? ????????????? (????????) ??????? ??? l=l_? .

Затем следует определить сумму квадратов расстояний между соответствующими точками желаемой и скорректированной частотными характеристиками:

(1.23)

Минимизируя величину Е с помощью одного из методов поиска экстремума, можно получить наилучшее приближение к желаемой характеристике при выбранном законе управления D(z).

? ?????????? ????? ?????? ????????? ??????? ???????????? R(l _? ) и рассматривать критерий оптимизации в виде

(1.24)

При использовании ЛЧХ следует задаваться значениями желаемых характеристик ЛАХ и ЛФХ в m точках для выбранных значений псевдочастоты l_к , ?=1, 2,…, m и строить критерий как сумму квадратов отклонений ЛАХ и ЛФХ разомкнутой скорректированной системы от желаемой:

??? L(l _к ) и j(l_к ) — значения желаемых ЛАХ и ЛФХ;

L _?? (l_к ) ? j_?? (l_к ) — ???????? ????????????????? ??? ? ???;

R(l _? ) и K_n — ??????? ????????????.

При выборе параметров закона управления по критериям Е, Е ₁ , Е₂ можно варьировать как постоянные времени форсирующих или инерционных звеньев, так и коэффициенты передаточной функции D(z), т.е. задача синтеза сводится к перебору различных структур и параметров, физически реализуемых D(z), и выбору D(z) простейшей структуры.

При машинных методах синтеза в качестве исходных законов управления принимают функции минимальной сложности и увеличивают их размерность до тех пор, пока не будет достигнуто приближение исходной частотной характеристики системы к желаемому виду. В этом случае в качестве исходных передаточных функций последовательного корректирующего устройства можно принимать функции вида

(1.26)

2 ?????????? ?????????? ???????? ? ????? Maple

2.1 Получение дискретной модели непрерывной системы

2.1.1 ????????? diskretA — ????????? ?????????? ??????? ?????????.

??????:

diskretA(?,?0)

?????????:

• А — матрица состояния непрерывной системы;
• Т0 — ???? ???????????.

????????:

Процедура вычисляет матрицу состояния дискретной системы по известной матрице состояния размерности (n? n) ??????????? ??????? ? ????? ??????????? ?? ???????, ??????????? ? ?????? 1.1. ??????????? ???????? ??????? ????? ?? ???????????.

Пример:

• diskretA(matrix(2,2,[0,1,2.268,-0.03]),0.1);

• [1.011350092 .1002280116]

[ ]

[.2273171304 1.008343251]

2.1.2 Процедура diskretВ — получение дискретной матрицы управления.

Формат:

diskretВ(А,В,Т0)

Параметры:

• А — матрица состояния непрерывной системы;
• В — ??????? ?????????? ??????????? ???????;
• Т0 — такт квантования.

Описание:

????????? ????????? ??????? ?????????? ?????????? ??????? ?? ????????? ??????? ????????? ??????????? (n? n), матрице управления размерности (n?m) непрерывной системы и такту квантования по формуле, приведенной в пункте 1.1. Результатом является матрица такой же размерности, что и матрица управления непрерывной системы.

Пример:

• diskretB(matrix(2,2,[0,1,2.268,-0.03]),matrix(2,1,[0,-4.235]),0.1);

• [ -.4257409375]

[ ]

[.06093613489]

2.2 Получение матрицы передаточных функций

2.2.1 ????????? permatr — ????????? ??????? ???????????? ???????.

??????:

permatr(?,?,?)

?????????:

• ? — матрица состояния непрерывной или дискретной системы;
• В — ??????? ?????????? ??????????? ??? ?????????? ???????;
• C — ????????? ?????????? s ??? z, ???????????? ???????????? ??????? ????? ??????? ?????????? ?????????.

????????:

Процедура вычисляет матрицу передаточных функций дискретной или непрерывной системы n-го порядка согласно пункту 1.2 по формуле (1.7).

Результатом выполнения процедуры является матрица n-го порядка, элементами которой являются передаточные функции.

??????:

• permatr(matrix(2,2,[4,3,2,1]),matrix(2,2,[0,1,2,1]),z);

2.3 Построение частотных характеристик

дискретной и непрерывной систем

2.3.1 ????????? afch — ?????????? амплитудно-фазовой частотной характеристики дискретной и непрерывной систем.

??????:

afch(W,c,?0)

?????????:

• W — ???????????? ??????? ???????;
• C — или z, обозначающая АФЧХ какой системы необходимо построить;
• Т0 — ???? ??????????? ??? ?????????? ???????.

????????:

????????? ?????? ???? ?????????? ? ??????????? ?????? ???????? ????????, ????????? ? ?????? 1.3.

??????:

• afch(1/(4*s^2-1.8*s+2),s,0.1);
• Полученный график можно увидеть на рисунке А.1 приложения А.

2.3.2 ????????? lach — ?????????? логарифмической амплитудно-частотной характеристики дискретной и непрерывной систем.

??????:

lach(W, c, ?0, x2, y1, y2)

?????????:

• W — ???????????? ??????? ???????;
• с — ????????? ?????????? s ??? z, ???????????? ???? ????? ??????? ?????????? ?????????;
• Т0 — такт квантования для дискретной системы;
• x2 — ?????? ?????? ????????? ???????;
• y1 и y2 — границы изменения логарифмической амплитуды.

Описание:

Процедура строит ЛАЧХ дискретной и непрерывной систем согласно методике, описанной в пункте 1.3.

Пример:

• lach(1/(4*s^2-1.8*s+2),s,0.1,5,-50,0);

• Полученный график можно увидеть на рисунке А.1 приложения А.

2.3.3 ????????? lfch — ?????????? логарифмической фазо-частотной характеристики дискретной и непрерывной систем.

??????:

lfch(W, c, ?0, x2, y1, y2)

?????????:

• W — ???????????? ??????? ???????;
• с — ????????? ?????????? s ??? z, ???????????? ???? ????? ??????? ?????????? ?????????;
• Т0 — такт квантования для дискретной системы;
• x2 — ?????? ?????? ????????? ???????;
• y1 и y2 — границы изменения логарифмической фазы.

Описание:

Процедура строит ЛФЧХ дискретной и непрерывной систем согласно методике, описанной в пункте 1.3.

Пример:

• lfch(1/(4*s^2-1.8*s+2),s,0.1,3,0,Pi);

• Полученный график можно увидеть на рисунке Б1 приложения Б.

2.4 Анализ устойчивости

?????????? ? ??????????? ??????

2.4.1 ????????? klark — построение особых линий для определения области устойчивости дискретных систем.

Формат:

klark(А, В, К, x1, x2, y1, y2)

?????????:

• А — матрица состояния дискретной системы;
• В — ??????? ?????????? ?????????? ???????;
• К — матрица;
• x1 и x2 — ??????? ????????? ????????? ?1;
• y1 и y2 — ??????? ????????? ????????? ?2;

????????:

????????? ?????? ?????? ????? ??? ??????????? ??????? ???????????? ?????????? ?????? ?? ???????? ??????, ?????????? ? ?????? 1.4. ??? ??????? ??????? ? ?????????? ??? ?????????? ????????? ?????????? ?1 ? ?2.

??????:

??????????? ?????? ????? ??????? ?? ??????? ?.1 ?????????? ?.

2.4.2 Процедура gurvitz — построение особых линий для определения области устойчивости непрерывных систем.

Формат:

gurvitz(А, В, К, x1, x2, y1, y2)

Параметры:

• А — ??????? ????????? ??????????? ???????;
• В — матрица управления непрерывной системы;
• К — ???????;
• x1 ? x2 — пределы изменения параметра к1;
• y1 и y2 — пределы изменения параметра к2;

Описание:

Процедура строит особые линии для определения области устойчивости непрерывных систем по критерию Гурвица, описанному в пункте 1.4. При задании матрицы К необходимо два изменяемых параметра обозначить к1 и к2.

Пример:

график можно увидеть на рисунке В.1 приложения В.

2.4.3 ????????? ust — ????????? ???????????? ??????????? ? ?????????? ????????? ??????.

??????:

ust(A, B, K, c)

Параметры:

• ? — ??????? ????????? ??????????? ??? ?????????? ???????;
• В — матрица управления непрерывной или дискретной системы;
• К — ???????;
• с — или z, ??????? ?????????? ???????????? ????? ??????? ?????????? ???????.

Описание:

Процедура оценивает устойчивость непрерывной и дискретной замкнутых систем по корневому критерию.

Процедура возвращает строковую переменную,

??????????? ????????:

• ust — система устойчива;
• noust — система не устойчива;
• nagr — система находится на границе устойчивости.

Пример:

ust(matrix(2, 2, [0,1,2.268,-0.03]), matrix(2,1,[0,-4.235]),

matrix(1, 2, [1,0]), z);

noust

2.5 Синтез дискретных систем

2.5.1 ????????? sintez1 — определяет коэффициенты корректи-рующего звена.

Формат:

Sintez1(W, Wg, a, T0)

Параметры:

• W — ???????? ???????????? ???????;
• Wg — вектор желаемых значений АФЧХ при определенных значениях частоты;
• А — ?????? ???????? ???????;
• T0 — такт квантования.

Описание:

????????? ?????????? коэффициенты корректирующего звена, реализующего первый закон управления (формула 1.26) по квадратичному критерию (1.23).

??????:

W := .5*(-93478.39101*z-.1150000000e3*z^2

+902.6600000*z^3+1026.926837)/(z^5-.5570000000*z^4-

124.6542298*z^3+46.10663267*z^2+328.8088091*z-4.226757788)

a:=vector(3,[10,100,1000]): Wg:=vector(3,[1,-1,-4]): ?0:=0.063:

• sintez1(W, Wg, a, t0);

2.5.2 Процедура sintez2 — ?????????? ???????????? ????????-??????? ?????.

??????:

Sintez1(W, Wg, a, T0)

?????????:

• W — исходная передаточная функция;
• Wg — ?????? ???????? ???????? ???? ??? ???????????? з???????? ???????;
• а — вектор значений частоты;
• T0 — ???? ???????????.

????????:

Процедура возвращает ???????????? ??????????????? ?????, ???????????? ?????? ????? ?????????? (??????? 1.26) ?? ????????????? ???????? (1.24).

??????:

W := .5*(-93478.39101*z-.1150000000e-3*z^2+902.6600000*z^3

+1026.926837)/(z^5-.5570000000*z^4-124.6542298*z^3

+46.10663267*z^2 +328.8088091*z-4.226757788)

a:=vector(3,[10,100,1000]): Wg:=vector(3,[1,-1,-4]): Т0:=0.063:

• sintez2(W, Wg, a, t0);

3 Апробация библиотеки процедур SSO на примере

самолета «Боинг-747»

Для примера взята система стабилизации линейного набора высоты. Уравнения системы имеют вид (1.1), матрицы А и В показаны на (рис. 3.1).

Ниже представлено:

1. Нахождение дискретных матриц В (рис.3.1) и А (рис.3.2).

2. Построение особых линий устойчивости по критерию Кларка для дискретных систем (рис.3.2).

3. Нахождение передаточных матриц непрерывной и дискретной систем (рис.3.3).

4. Построение ЛАЧХ и ЛФЧХ непрерывной (рис.3.4) и дискретной (рис.3.5) систем.

5. Построение особых линий устойчивости по критерию Гурвица для непрерывных систем (рис.3.6).

6. Нахождение коэффициентов корректирующего устройства наиболее приближающего желаемую АФЧХ к исходной по двум критериям (рис.3.7).

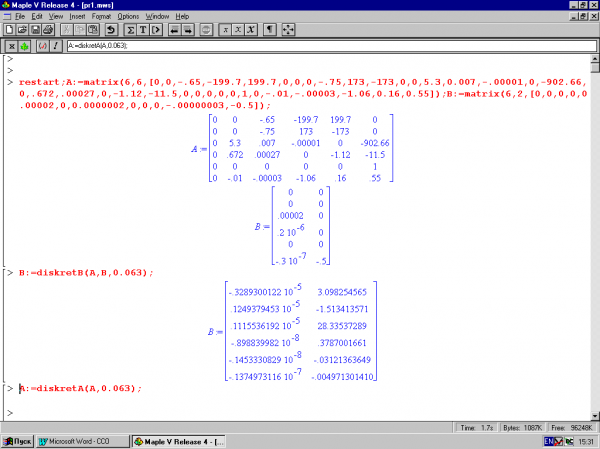
Рис. 3.1

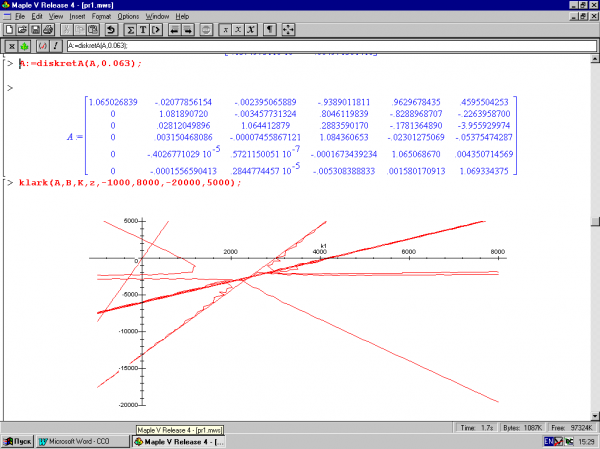
Рис. 3.2

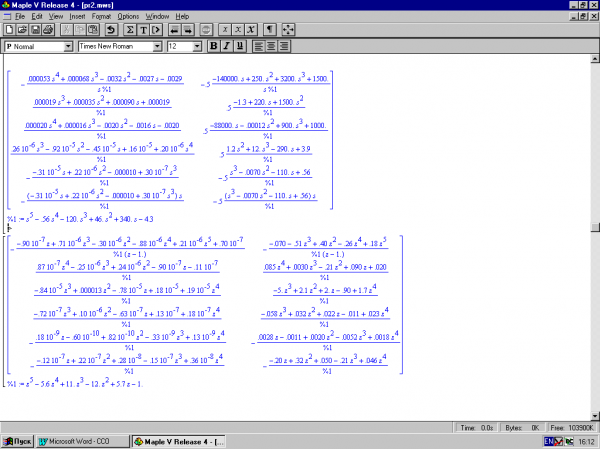
Рис. 3.3

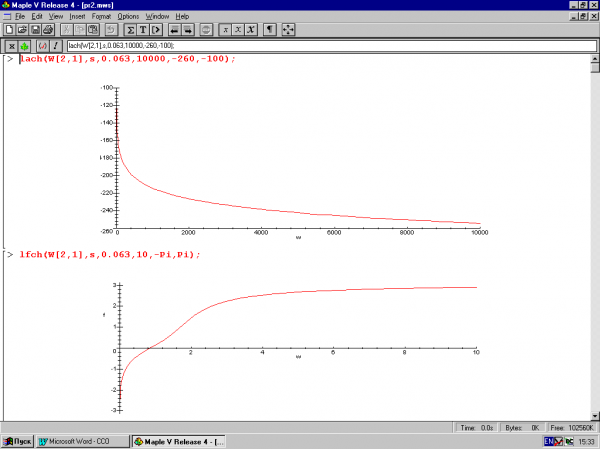
Рис. 3.4

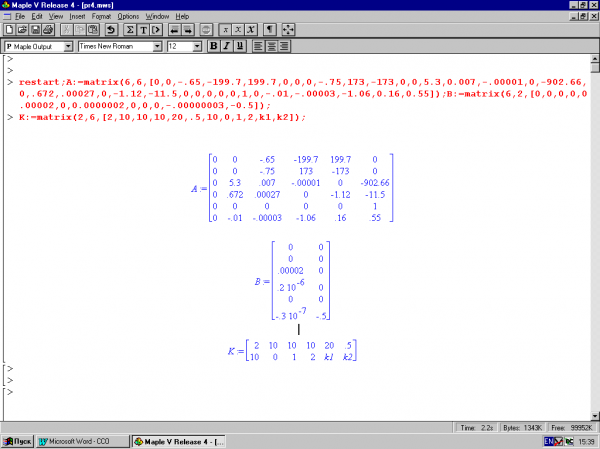
Рис. 3.5

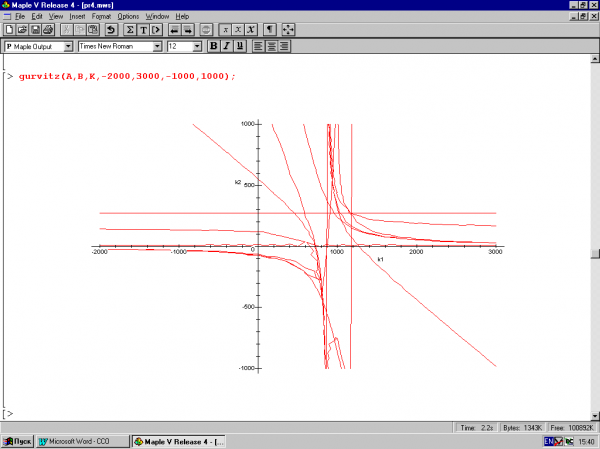
Рис. 3.6

Список литературы

[Электронный ресурс]//URL: https://inzhpro.ru/kursovaya/sistema-stabilizatsii/

1. ????????? ?.?., ?????????? ?.?. ?????????????? ?????? ???????????? ????????? ??????????? ?????????.- ?.: ??????????????,1986

2. Бесекерский В.А. Цифровые автоматические системы.- М.: Наука, 1976

3. ??????? ?.?., ???????? ?.?., ????? ?.?. ??????? ???????????? ??.- ?.: ???,1989

4. Куо Б. Теория и проектирование цифровых систем управления. — М.:Машиностроение,1986

5. ??????? ?.?. ????? ??? ?????????????? ?????? ??????????????? ?????????????. -?.: ??????????????, 1989

6. Дьяконов В.П. Математическая система MAPLE V R3/R4/R5.-?.:?????,1998