Непрерывные случайные величины

метки: Величина, Случайный, Непрерывный, Событие, Вероятность, Функция, Называть, Доказательство

Непрерывные случайные величины — раздел Математика, Событие и вероятность 1. Интегральная Функция Распределения. Для Непрерывной Случайной Величины В О…

1. Интегральная функция распределения. Для непрерывной случайной величины в отличие от дискретной нельзя построить таблицу распределения. Поэтому непрерывные случайные величины изучают другим способом, который мы сейчас рассмотрим. Пусть X — непрерывная случайная величина с возможными значениями из некоторого интервала (а; b) и х — действительное число. Под выражением Х<х понимается событие «случайная величина Л’ приняла значение, меньшее х». Вероятность этого события Р(Х< х) есть некоторая функция переменной х

Р(х) = Р(Х

Определение.

F(х) = Р(Х < х).

Отметим, что функция распределения совершенно также определяется для дискретных случайных величин.

Укажем свойства, которыми обладает функция F(х).

1. 0 £ F(х) £ 1.

Это свойство следует из того, что F(х) есть вероятность.

2. F(х) — неубывающая функция, т.е. если х ₁ < х₂ , то F(х_} ) £F(х₂ ).

Доказательство. Предположим, что х ₁ <х₂ . Событие «X примет значение, меньшее х ₂ » можно представить в виде суммы двух несовместимых событий: «X примет значение, меньшее х ₁ и «X примет значение, удовлетворяющее неравенствам х ₁ £ Х< х ₂ ». Обозначим вероятности последних двух событий соответственно через Р(Х< х ₁ ) и Р(х ₁ £Х<х₂ ). По теореме о вероятности суммы двух несовместимых событий

Р(Х < х ₂ )

откуда с учетом (9.4)

Р(х ₁ £Х<х₂ )= F(х₂ )- F(х₁ ). (9.5)

Так как вероятность любого события есть число неотрицательное, то Р(х ₁ £Х<х₂ )³ 0 и, значит, F(х₂ )³F(х₁ ).

Формула (9.5) утверждает свойство 3.

5. Вероятность попадания случайной величины Х в полуинтервал [а; b) равна разности между значениями функции распределения в правом и левом концах интервала (а; b):

Р(а£Х<b) = F(b)-F(а).

Пример 9.9.

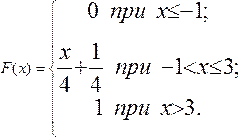
Найдем вероятности того, что в результате испытания X примет значение, принадлежащее полуинтервалу [0; 2).

х

Решение. Так как на полуинтервале [0; 2) F(х) = 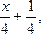то

Р( 0£Х< 2) = F( 2)-F( 0) =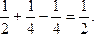

В дальнейшем случайную величину X будем называть непрерывной, если непрерывна ее функция распределения F (х ) с непрерывной или кусочно-непрерывной производной.

4. Вероятность того, что непрерывная случайная величина X примет какое-либо заранее заданное значение, равна нулю:

Р(Х = х ₁ ) = 0. (9.7)

х ₂ = х

Р(х ₁ £ X < х ₁ + Dх ) = F (х ₁ + Dх ) — F(х ₁ ).

(9.8)

Так как F(х ) — непрерывная функция, то, перейдя в (9.8) к пределу при Dх ®0, получим искомое равенство (9.7).

Из свойства 4 следует свойство 5.

5. Вероятности попадания непрерывной случайной величины в интервал, сегмент и полуинтервал с одними и теми же концами одинаковы

Р(a<X <b

Если возможные значения случайной величины X принад­лежат интервалу (а; b), то

Доказательство. 1) Пусть х ₁ £а. Тогда событие Х< х ₁ невозможно, и, следовательно, вероятность его равна нулю.

2) Пусть х ₂ ³ b. Тогда событие X < х₂ достоверно, и, следовательно, вероятность его равна 1.

Следствие.

F(- ¥) =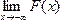=0; F( ¥) =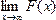== 1.

Дифференциальной функцией распределения

Так как F(х ) — неубывающая функция, то f(х ) ³ 0 (см. подразд. 3.7, п. 1).

Теорема 9.3.

Р(а<Х<b)=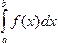 . (9.10)

Доказательство. Так как F(х )является первообразной для f(х ), то на основании формулы Ньютона— Лейбница (см. подразд. 4.4, п. 2)

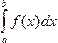=F(b)-F(а). (9.11)

Теперь с учетом соотношений (9.6), (9.9), (9.11) получим искомое равенство.

Р(а<X<b)

Следствие.

Р(-а<Х<a)= Р(

Заменяя в формуле (9.11) а на -¥ и b на х , получаем

F(x)-F(- ¥)= .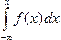

откуда, в силу найденного выше следствия (см. п. 1),

F(x)= .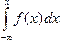

Формула (9.13) дает возможность отыскать интегральную функцию распределения F(x) по ее плотности вероятности.

Отметим, что из формулы (9.13) и из только что отмеченного следствия вытекает, что

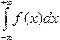
Пример 9.10

f(x)=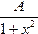

Требуется найти коэффициент А, функцию распределения F(х) и вероятность попадания случайной величины Х в интервал (0; 1).

Решение. Коэффициент А найдем, воспользовавшись соотношением (9.14).

Так как

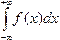
= A arctg (+¥)-A arctg (-¥)=Аp ,

то Аp = 1, откуда А = 1/p.

Применяя формулу (9.13), получаем функцию распределения F(х) :

F(х) = 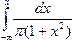=A arctg x 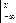= [ arctg x- arctg (-¥)]=

Наконец, формулы (9.6) и (9.9) с учетом найденной функции F(х) дают

P (0< x < 1)= F( 1) — F( 0) = .

Все темы данного раздела:

Цель: Изучить основные понятия теории вероятности План: 1.Основные понятия. Определение вероятности 2. Свойства вероятности 3. Вопросы для контроля знаний и подв

Определение 1. Суммой событий А и В называют событие С = А + В, состоящее в наступлении, по крайней мере, одного из событий А или

Теорема 8.5. Вероятность события А, которое может наступить лишь при условии появления одного из п попарно несовместимых событий В1, В2,… , В

Пусть в условиях рассуждения, относящегося к формуле полной вероятности, произведено одно испытание, в результате которого произошло событие А. Спрашивается, как изменились (в связи с тем, ч

1. Дайте определения противоположным, независимым, несовместным событиям. Приведите примеры таких событий. 2. Что называется полной группой событий? 3. Сформулируй

1. Понятие «случайные величины». Определение 1. Случайной величиной называют переменную величину, которая в зависимости от исхода испытания случайн

1. Понятие математического ожидания.Закон распределения полностью задает дискретную случайную величину. Однако часто встречаются случаи, когда закон распределения случайной величин

1.Математическое ожидание постоянной величины С равно этой величине. Постоянную С можно рассматривать как дискретную случайную величину, принимающую лишь одно зн

1. Понятие дисперсии.Математическое ожидание не дает полной характеристики закона распределения случайной величины. Покажем это на примере. Пусть заданы две дискретные случайные ве

Определение. Средним квадратическим отклонением s(X) случайной величины X называется корень квадратный из ее дисперсии: s(X) =

Определение 1. Начальным моментом порядка k случайной величины X называют математическое ожидание случайной величины Xk, где k — натуральное

Определение 1. Математическим ожиданием непрерывной случайной величины Х с плотностью вероятности f(x) называют величину несобственного интеграла (если он сход

1. Биномиальное распределение.Пусть производится п испытаний, причем вероятность появления события А в каждом испытании равна р и не зависит от исхода других и

Если число испытаний п велико, то вычисления по формуле Бернулли становятся затруднительными. Лаплас получил важную приближенную формулу для вероятности Рn(т) появления соб

Гипергеометрическое распределение имеет место при выборочном контроле конечной совокупности объектов объёма N по альтернативному признаку. Каждый контролируемый объект классифицируетс

Мы приступаем к изучению элементов математической статистики, в которой разрабатываются научно обоснованные методы сбора статистических данных и их обработки. 1. Генеральная совоку

1. Выборка как набор случайных величин.Пусть имеется некоторая генеральная совокупность, каждый объект которой наделен количественным признаком X. При случайном извлечении о

Цель: Изучить основные понятия теории графов План: 1. Основные понятия и определения графа и его элементов 2. Деревья. Лес. Бинарные деревья 3. Способы задания г

С вершины дорога вперед — только вниз. Я. Таранов Деревомназывают конечный связный граф с выделенной вершиной (корнем),не имеющий циклов (

В этом проглядывается талант исследователя охватить значительные районы явлений с помощью немногочисленных допущений, представить разносторонние совокупности предметов и процессов в сжатой, компакт

Храни порядок, и порядок сохранит тебя. Латинская формула Сети получили широкое практическое применение потому, что они являются естественным и удобным способом изображения