1.1 Линейное программирование
Линейное программирование — это направление математического программирования, изучающее методы решения экстремальных задач, которые характеризуются линейной зависимостью между переменными и линейным критерием. Такие задачи находят обширные приложения в различных сферах человеческой деятельности. Систематическое изучение задач такого типа началось в 1939-1940 гг. в работах Л.В. Канторовича.
К математическим задачам линейного программирования относят исследования конкретных производственно-хозяйственных ситуаций, которые в том или ином виде интерпретируются как задачи об оптимальном использовании ограниченных ресурсов.
Круг задач, решаемых при помощи методов линейного программирования достаточно широк. Это, например:
- задача об оптимальном использовании ресурсов при производственном планировании;
- задача о смесях (планирование состава продукции);
- задача о нахождении оптимальной комбинации различных видов продукции для хранения на складах (управление товарно-материальными запасами или);
— Линейное программирование — наиболее разработанный и широко применяемый раздел математического программирования (кроме того, сюда относят: целочисленное, динамическое, нелинейное, параметрическое программирование).
Это объясняется следующим:
- математические модели большого числа экономических задач линейны относительно искомых переменных;
- данный тип задач в настоящее время наиболее изучен. Для него разработаны специальные методы, с помощью которых эти задачи решаются, и соответствующие программы для ЭВМ;
- многие задачи линейного программирования, будучи решенными, нашли широкое применение;
— некоторые задачи, которые в первоначальной формулировке не являются линейными, после ряда дополнительных ограничений и допущений могут стать линейными или могут быть приведены к такой форме, что их можно решать методами линейного программирования.
Экономико-математическая модель любой задачи линейного программирования включает: целевую функцию, оптимальное значение которой (максимум или минимум) требуется отыскать; ограничения в виде системы линейных уравнений или неравенств; требование неотрицательности переменных.
В общем виде модель записывается следующим образом:
целевая функция
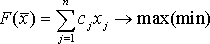 (1.1)
(1.1)
«Разработка методической поддержки базового курса информатики ...
... основ программирования в базовом курсе информатики. Создать сайт учителя. Структура дипломной работы. конспекты уроков по темам, в которых и зложение теоретического материала сопровождается примерами и задачами с ... шестнадцатеричной форме. С ними трудно работать, но созданные с их помощью высококвалифицированным программистом программы занимают меньше места в памяти и работают быстрее. С помощью ...
при ограничениях
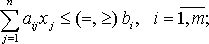 (1.2)
(1.2)
требования неотрицательности
![]() (1.3)
(1.3)
где x j — переменные (неизвестные);
![]() — коэффициенты задачи линейного программирования.
— коэффициенты задачи линейного программирования.
Задача состоит в нахождении оптимального значения функции (1.1) при соблюдении ограничений (1.2) и (1.3).
Систему ограничений (1.2) называют функциональными ограничениями задачи, а ограничения (1.3) — прямыми.
Вектор, удовлетворяющий ограничениям (1.2) и (1.3), называется допустимым решением (планом) задачи линейного программирования. План, при котором функция (1.1) достигает своего максимального (минимального) значения, называется оптимальным.
1.2 Симплекс метод решения задач линейного программирования
Симплекс-метод был разработан и впервые применен для решения задач в 1947 г. американским математиком Дж. Данцигом.
Двумерные задачи линейного программирования решаются графически. Для случая N=3 можно рассмотреть трехмерное пространство и целевая функция будет достигать своё оптимальное значение в одной из вершин многогранника.
Допустимым решением (допустимым планом) задачи ЛП, данной в стандартной форме, называется упорядоченное множество чисел (х1, х2, …, хn), удовлетворяющих ограничениям; это точка в n-мерном
Множество допустимых решений образует область допустимых решений (ОДР) задачи ЛП. ОДР представляет собой выпуклый многогранник (многоугольник).
В общем виде, когда в задаче участвуют N-неизвестных, можно сказать, что область допустимых решений, задаваемая системой ограничивающих условий, представляется выпуклым многогранником в n-мерном пространстве и оптимальное значение целевой функции достигается в одной или нескольких вершинах.
Базисным называется решение, при котором все свободные переменные равны нулю.
Опорное решение — это базисное неотрицательное решение. Опорное решение может быть невырожденным и вырожденным. Опорное решение называется невырожденным, если число его ненулевых координат равно рангу системы, в противном случае оно является вырожденным.
Допустимое решение, при котором целевая функция достигает своего экстремального значения, называется оптимальным и обозначается ![]() .
.
Решить данные задачи графически, когда количество переменных более 3 весьма затруднительно. Существует универсальный способ решения задач линейного программирования, называемый симплекс-методом.
Симплекс-метод — это универсальный метод решения задач ЛП, представляющий собой итерационный процесс, который начинается с одного решения и в поисках лучшего варианта движется по угловым точкам области допустимых решений до тех пор, пока не достигнет оптимального значения.
С его помощью можно решить любую задачу линейного программирования.
В основу симплексного метода положена идея последовательного улучшения получаемого решения.
O Л. В. Канторовиче и линейном программировании
... линейных экстремальных задачах (знаменитой задаче фантреста) и о придуманном им методе разрешающих множителей для решения задач, которые позже стали называть задачами линейного программирования. ... анализа, был известный семинар Фихтенгольца-Канторовича на математико-механическом факультете ЛГУ, ... которого стояли В.И.Смирнов, Г.М.Фихтенгольц и, как основной мотор, - Л.В., а позже Г.П.Акилов, ...
Геометрический смысл симплексного метода состоит в последовательном переходе от одной вершины многогранника ограничений к соседней, в которой целевая функция принимает лучшее (или, по крайней мере, не худшее) значение до тех пор, пока не будет найдено оптимальное решение — вершина, где достигается оптимальное значение функции цели (если задача имеет конечный оптимум).
Таким образом, имея систему ограничений, приведенную к канонической форме (все функциональные ограничения имеют вид равенств), находят любое базисное решение этой системы, заботясь только о том, чтобы найти его как можно проще. Если первое же найденное базисное решение оказалось допустимым, то проверяют его на оптимальность. Если оно не оптимально, то осуществляется переход к другому, обязательно допустимому базисному решению. Симплексный метод гарантирует, что при этом новом решении целевая функция, если и не достигнет оптимума, то приблизится к нему (или, по крайней мере, не удалится от него).
С новым допустимым базисным решением поступают так же, пока не отыщется решение, которое является оптимальным.
Процесс применения симплексного метода предполагает реализацию трех его основных элементов:
1. способ определения какого-либо первоначального допустимого базисного решения задачи;
2. правило перехода к лучшему (точнее, не худшему) решению;
- критерий проверки оптимальности найденного решения.
Симплексный метод включает в себя ряд этапов и может быть сформулирован в виде четкого алгоритма (четкого предписания о выполнении последовательных операций).
Это позволяет успешно программировать и реализовывать его на ЭВМ. Задачи с небольшим числом переменных и ограничений могут быть решены симплексным методом вручную.
1.3. Двойственная задача линейного программирования
С каждой задачей линейного программирования можно некоторым образом сопоставить другую задачу ЛП, называемую двойственной по отношению к исходной (прямой).
Под двойственной задачей понимается вспомогательная задача линейного программирования, формулируемая с помощью определённых правил непосредственно из условий прямой задачи. Заинтересованность в определении оптимального решения прямой задачи путём решения двойственной к ней задачи обусловлена тем, что вычисления при решении ДЗ могут оказаться менее сложными. Трудоёмкость вычислений при решении ЗЛП в большей степени зависит от числа ограничений, а не от количества переменных.
Дадим определение двойственной задачи по отношению к прямой задаче линейного программирования, состоящей, в нахождении максимального значения функции
функции
f =c 1 x1 + c2 x2 + … + cn xn →max (1.4)
при условиях:
a 11 x1 + a12 x2 + … + a1n xn ≤ b121 x1 + a22 x2 + … + a2n xn ≤ b2
… (1.5) m1 x1 + am2 x2 + … + amn xn ≤ bmj ≥ 0 (j = 1, 2,… m, m ≤ n).
Задача, состоящая в нахождении минимального значения функции
Виды и способы приготовления теста
... сахара, иногда химических разрыхлителей и яиц. По консистенции пресное сдобное тесто напоминает песочное. Оно используется для изготовления пирогов и пирожков. Для приготовления сдобного пресного теста на 1 кг муки берут 2 ... углекислого газа, тесто 1-2 раза обминают. Для приготовления дрожжевого теста на каждый килограмм муки берут от 20 до 50 г дрожжей. Чем сдобнее тесто, тем больше нужно ...
f*=b 1 y1 + b2 y2 + … + bm ym →min (1.6)
при условиях:
a 11 y1 + a12 y2 + … + am1 ym ≥ c112 y1 + a22 y2 + … + am2 ym ≤ c2
… (1.7) 1n y1 + a2n y2 + … + amn ym ≤ cmi ≥ 0 (i = 1, 2, … k ≤ m)
называется двойственной по отношению к задаче (1.4) — (1.5).
Задачи (1.4) — (1.5) и (1.6) — (1.7) образуют пару задач, называемую в линейном программировании двойственной парой. Сравнивая две сформулированные задачи, видим, что двойственная задача составляется согласно следующим правилам:
Целевая функция исходной задачи задается на максимум, а целевая функция двойственной — на минимум.
1. Матрица
 (1.8)
(1.8)
2. составленная из коэффициентов при неизвестных в системе ограничений (1.5) исходной задачи, и аналогичная матрица
 (1.9)
(1.9)
в двойственной задаче получаются друг из друга транспонированием (т.е. заменой строк столбцами, а столбцов — строками).
3. Число переменных в двойственной задаче равно числу ограничений в системе (1.5) исходной задачи, а число ограничений в системе (1.7) двойственной задачи — числу переменных в исходной задаче.
4. Коэффициентами при неизвестных в целевой функции (1.6) двойственной задачи являются свободные члены в системе (1.5) исходной задачи, а правыми частями в соотношениях системы (1.7) двойственной задачи — коэффициенты при неизвестных в целевой функции (1.4) исходной задачи.
— Если i-е соотношение в системе (1.5) исходной задачи является неравенством, то j-я переменная двойственной задачи y j ≥ 0. В противном случае переменная уj может принимать как положительные, так и отрицательные значения.
Двойственные пары задач обычно подразделяют на симметричные и несимметричные. В симметричной паре двойственных задач ограничения (1.5) прямой задачи и соотношения (1.7) двойственной задачи являются неравенствами вида «![]() ». Таким образом, переменные обеих задач могут принимать только лишь неотрицательные значения.
». Таким образом, переменные обеих задач могут принимать только лишь неотрицательные значения.
Двойственные пары задач обычно подразделяют на симметричные и несимметричные. В симметричной паре двойственных задач ограничения (1.5) прямой задачи и соотношения (1.7) двойственной задачи являются неравенствами вида «![]() ». Таким образом, переменные обеих задач могут принимать только лишь неотрицательные значения.
». Таким образом, переменные обеих задач могут принимать только лишь неотрицательные значения.
Если одна из задач двойственной пары (1.4) — (1.5) или (1.6) — (1.7) имеет оптимальный план, то и другая имеет оптимальный план, и значения целевых функций задач при их оптимальных планах равны между собой, т.е. f max = f*min.
Фабрика ООО «Мельник» специализируется на выпуске двух сортов теста: бисквитное и песочное. Для изготовления теста используются такие ингредиенты как яйца и сахар, так же затрачивается и ресурсы труда. Для изготовления бисквитного теста требуется 5 штук яиц и 0,3 килограмма сахара, для изготовления затрачивается 15 минут. А для изготовления песочного теста потребуется 2 яйца, 0,25 килограмма сахара и 30 минут затраченного времени. Стоимость 1 кг бисквитного теста 30 руб., а песочного 20 руб. Общий запас яиц равен 1000 шт., 75 кг сахара и 125 часов трудовых ресурсов.
2.1 Построение экономико-математической модели
- Переменные задачи.
В задаче требуется установить, сколько продукции каждого вида надо производить, поэтому искомыми величинами, а значит, и переменными задачи являются суточные объемы производства каждого вида продукции:
х 1 — суточный объем производства бисквитного теста, (кг);
х 2 — суточный объем производства песочного теста, (кг).
- Целевая функция.
В условии задачи сформулирована цель — добиться максимального дохода от реализации продукции, т.е. критерием эффективности служит параметр суточного дохода, который должен стремиться к максимуму. Чтобы рассчитать величину суточного дохода от продажи продукции обоих видов, необходимо знать объемы производства, т.е. x 1 и х2 кг продукции в сутки, а также цены на продукцию бисквитного и песочного теста — согласно условию 30 и 20 руб. за 1 кг продукции соответственно. Таким образом, доход от продажи суточного объема производства продукции бисквитного теста равен 30х1 руб. в сутки, а от продажи песочного теста — 20х2 тыс. руб. в сутки. Поэтому запишем целевую функцию в виде суммы дохода от продажи продукции бисквитного и песочного теста.
![]() (руб.).
(руб.).
- Ограничения.
Возможные объемы производства продукции х 1 и х2 ограничиваются следующими условиями:
- количество яиц, сахара и трудовых ресурсов, израсходованных в течение суток на производство теста обоих видов, не может превышать запаса этих ингредиентов на складе;
- объем производства продукции не может быть выражен отрицательными значениями.
Запишем эти ограничения в математической форме.
Ограничение по расходу яиц имеет вид:
![]() (т/сутки).
(т/сутки).
Левая часть ограничения — это расчет расхода яиц на производство теста обоих видов. Расход яиц на производство 1 кг бисквитного теста — 5 шт.; на производство 1 кг песочного теста — 2 шт. Тогда на производство х 1 кг бисквитного теста и х2 кг песочного теста потребуется (5х1 + 2x2 ) шт. яиц. Правая часть ограничения — это величина запаса яиц на складе — 1000 шт.
Аналогична запись ограничения по расходу сахара:
![]() (кг).
(кг).
Так же ограничение по трудовым ресурсам имеет вид:
![]() (чел.-ч.)
(чел.-ч.)
Неотрицательность объемов производства задается как ![]()
Таким образом, математическая модель задачи имеет вид:
![]() ;
;
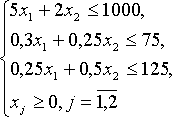
Экономико-математическая модель задачи состоит в том, чтобы найти такой план производства продукции ![]() , удовлетворяющий системе ограничений, при котором целевая функция принимает максимальное значение.
, удовлетворяющий системе ограничений, при котором целевая функция принимает максимальное значение.
2.2 Определение оптимального плана производства симплексным методом
Приведем задачу к каноническому виду. Для этого в ограничения задачи введем дополнительные переменные х 3 , х4 , х5 и перепишем условие задачи в виде уравнений:
![]()
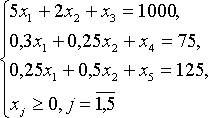
В качестве базисных переменных возьмем х 3 , х4 , х5 , тогда небазисные — х1 , х2 . Полагаем х1 = х2 = 0, тогда х3 =1000, х4 =75, х5 =125.
- я итерация.
Составляем первую симплексную таблицу, соответствующую исходному опорному решению (таблица 3):
![]()
или
![]()
Таблица 3
|
c i |
БП |
30 |
20 |
0 |
0 |
0 |
b i |
|
x 1 |
x 2 |
x 3 |
x 4 |
x 5 |
|||
|
0 |
x 3 |
5 |
2 |
1 |
0 |
0 |
1000 |
|
0 |
x 4 |
0,3 |
0,25 |
0 |
1 |
0 |
75 |
|
0 |
x 5 |
0,25 |
0,5 |
0 |
0 |
125 |
|
|
D j |
— 30 |
— 20 |
0 |
0 |
0 |
0 |
|
Все строки таблицы, за исключением индексной, заполняем по данным системы ограничений и целевой функции. Элементы последней строки рассчитываем:
![]()
![]()
![]()
![]() и т.д.
и т.д.
В индексной строке две отрицательные оценки, значит, найденное решение не является оптимальным и его можно улучшить. В качестве разрешающего столбца следует принять столбец переменной х1 :
![]() , т.е. k =1.
, т.е. k =1.
За разрешающую строку принимаем строку переменной х3 :
![]() , т.е. s =1.
, т.е. s =1.
Разрешающим является элемент а11 =5, т.е. вводим в базис переменную х1 , выводим х3 .
-я итерация.
Формируем следующую симплексную таблицу (таблица 4)
Таблица 4
|
c i |
БП |
30 |
20 |
0 |
0 |
0 |
b i |
|
x 1 |
x 2 |
x 3 |
x 4 |
x 5 |
|||
|
30 |
x 1 |
1 |
0,4 |
0,2 |
0 |
0 |
200 |
|
0 |
x 4 |
0 |
0,13 |
-0,06 |
1 |
0 |
15 |
|
0 |
x 5 |
0 |
0,4 |
-0,05 |
0 |
1 |
75 |
|
D j |
0 |
— 8 |
6 |
0 |
0 |
6000 |
|
Из таблицы 4 находим опорный план:
![]() ,
, ![]()
В индексной строке таблицы 4 имеется одна отрицательная оценка. Полученное решение можно улучшить. Разрешающим элементом является а22 =0,13
-я итерация.
Формируем следующую симплексную таблицу (таблица 5).
|
c i |
БП |
30 |
20 |
0 |
0 |
0 |
b i |
|
x 1 |
x 2 |
x 3 |
x 4 |
x 5 |
|||
|
30 |
x 1 |
1 |
0 |
0,38 |
-3,07 |
0 |
153,8 |
|
20 |
x 2 |
0 |
1 |
-0,4 |
7,7 |
0 |
115,4 |
|
0 |
x 5 |
0 |
0 |
0,13 |
-3,07 |
1 |
28,8 |
|
D j |
0 |
0 |
2,3 |
61,5 |
0 |
6923 |
|
Из таблицы 5 находим опорный план:
![]() ,
, ![]()
Так как все оценки свободных переменных положительные, найденное решение является оптимальным:
![]()
![]()
Максимальная прибыль составит 6923 рублей, при этом необходимо произвести 153,8 кг бисквитного теста и 115,4 кг песочного теста. В оптимальном плане ресурсы яиц и сахара равны нулю (х3 =х4 =0), так как они используются полностью. А резерв трудовых ресурсов х5 = 28,8, что свидетельствует о излишках.
Построение двойственной задачи
Оценки, приписываемые каждому виду ресурсов, должны быть такими, чтобы оценка всех используемых ресурсов была минимальной, а суммарная оценка ресурсов на производство единицы продукции каждого вида — не меньше цены единицы продукции данного вида.
Обозначим через y1 — двойственную оценку дефицитности яиц, через y2 — сахара, y3 — трудовых ресурсов. Тогда прямая и двойственная задачи формулируются:
прямая задача
![]()
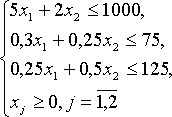
двойственная задача
![]()
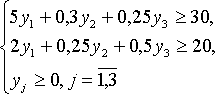
Решение прямой задачи дает оптимальный план производства песочного и бисквитного теста, а решение двойственной задачи — оптимальную систему оценок ресурсов, используемых для производства:
![]()
![]()
Двойственные оценки ресурсов yi * — это оценочные коэффициенты Dj дополнительных переменных х3 , х4 , х5 в последней симплексной таблице.
Исходя из анализа оптимальных двойственных оценок, можно сделать
Ресурсы яиц и сахара используются полностью. Полному использованию этих ресурсов соответствуют полученные оптимальные оценки y1 , y2 , отличные от нуля. Значит, трудовые ресурсы недоиспользуются (х5 = 28,8 чел.-ч.).
.3 Решение задачи оптимизации в табличном процессоре MS Excel
Для решения задач линейного программирования в MS Excel изначально мной был построен шаблон для ввода исходных данных.
Далее оптимальный план для поставленной задачи нашла с помощью функции «Поиск решения».
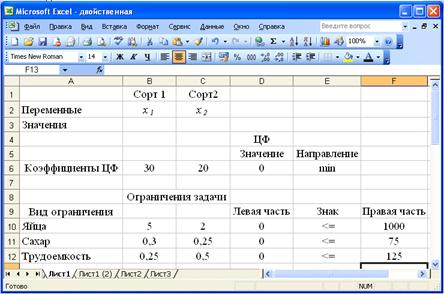
Рисунок 1 — Экранная форма задачи
Используя обозначения соответствующих ячеек в Excel, для расчета целевой функции была использована формула СУММПРОИЗВ, как сумма произведений соответствующих ячеек на соответствующие значения.
Таблица 7
|
Левая часть ограничения |
Формула Excel |
|
5x 1 +2x2 |
=СУММПРОИЗВ ($B$3:$C$3; B10:C10) |
|
0,3x+0,25x 2 |
=СУММПРОИЗВ ($B$3:$C$3; B11:C11) |
|
0,25x 1 +0,5x2 |
=СУММПРОИЗВ ($B$3:$C$3; B12:C12) |
Отчете по результатам (рис. 4).
В этом отчете в столбцах «Результат» можно увидеть оптимальный план решения задачи: максимальную прибыль фабрики и производство двух сортов теста. А так же количество израсходованных ресурсов
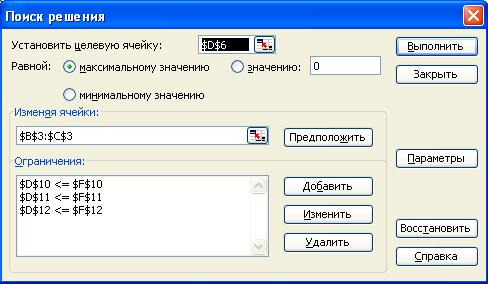
Рисунок 2 — Окно «Поиск решения» после ввода всех необходимых данных
В конечном итоге у нас получился оптимальный план решения задачи.
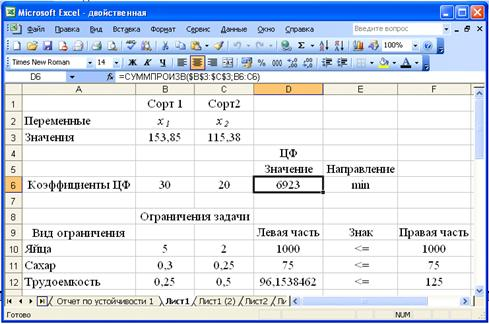
Рисунок 3 — Экранная форма после получения решения
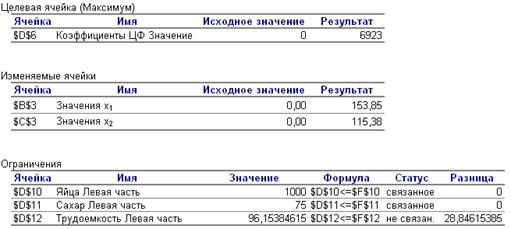
Рисунок 4 — Отчет по результатам
Отчет по устойчивости (рис. 5).В этом отчете можно увидеть оптимальное решение по производству теста. Так же допустимые приращения коэффициентов целевой функции, при которых сохраняется прежнее оптимальное решение и др.
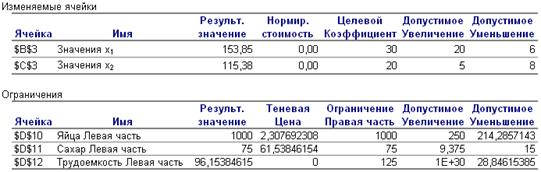
Рисунок 5 — Отчет по устойчивости
Отчет по пределам изменений представлен на рис. 6.
В отчете показано, в каких пределах может изменяться выпуск продукции, вошедший в оптимальное решение, при сохранении структуры оптимального решения. Там же даны соответствующие оптимальные значения целевой функции.
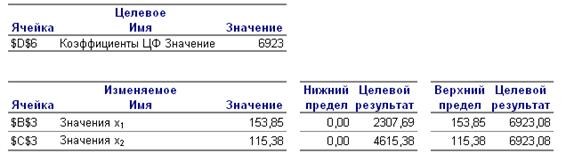
Рис. 6 — Отчет по пределам
В ходе курсовой работы были решены следующие основные задачи построена экономико-математическая модель задачи, определен оптимальный план производства симплексным методом и решена задача оптимизации в табличном процессоре MS Excel.
Максимальная прибыль фабрики по изготовлению теста составила 6923 рублей, при этом необходимо произвести 153,8 кг бисквитного теста и 115,4 кг песочного теста.
Исходя из анализа оптимальных двойственных оценок, можно сделать следующие выводы:
Запасы яиц и сахара используются полностью. Полному использованию этих ресурсов соответствуют полученные оптимальные оценки y1 , y2 , отличные от нуля. Значит, трудовые ресурсы недоиспользуются в размере 28,8 чел.-ч.
Увеличение количества яиц на 1 шт. приведет к тому, что появится возможность найти новый оптимальный план производства продукции, при котором общая прибыль возрастает на 2,31 руб. и станет равной 6923 + 2,31 = 6925,31 руб. Анализ полученных оптимальных значений новой прямой задачи показывает, что это увеличение общей прибыли достигается за счет увеличения производства бисквитного теста на 0,38 руб. и сокращения выпуска бисквитного теста на 0,4 руб. Вследствие этого использование трудовых ресурсов увеличится на 0,13 руб.
Точно так же увеличение на 1 кг. количества сахара позволит перейти к новому оптимальному плану производства, при котором прибыль возрастет на 61,54 руб. и составит 6984,5 руб., что достигается за счет уменьшения выпуска бисквитного теста на 3,07 руб. и увеличения выпуска песочного теста на 7,7 руб., причем объем используемых трудовых ресурсов увеличится на 3,07 руб.
Уменьшение количество запасов сахара на 15 кг приведет к тому что появится новый оптимальный план производства при котором общая прибыль уменьшится на 923 рубля, т.е. станет равен 6000 рублей.
Увеличение цены бисквитного теста с 30 до 40 рублей за 1 кг не изменит оптимальное решение, т.к. при анализе в отчете по устойчивости «Допустимое увеличение» равно 20, а это значит что при увеличении цены до 50 рублей за кг оптимальное решение не будет изменено.
симплекс производство двойственный excel
1. Акулич И.Л. Математическое программирование в примерах и задачах. М., 2007.
. Грешилов А.А. Прикладные задачи математического программирования. М., 2009.
3. Конюховский П.В. Математические методы исследования операций в экономике. — СПб: Питер, 2010
. Хемди А. Таха. Введение в исследование операций. 7-е изд. — М.: «Вильямс», 2007.
