Метод половинного деления

метки: Деление, Половинный, Оценка, Погрешность, Функция, Корень, Отрезка, Значение

, названного так в честь великого французского математика и механика Блеза Паскаля, создавшего в 1642 г. первую счетную машину. В 1971 г. Н. Вирт выпустил описание своего языка, а в 1975 г. было разработано руководство для пользователей версии Паскаля, которая практически легла в основу стандарта языка. Но стандарт языка появился только в 1982 г.

Предназначенный для обучения, язык оказался очень простым и одновременно строгим. Однако вскоре выяснилось, что он также является достаточно эффективным в самых различных приложениях. Pascal поддерживает самые современные методологии проектирования программ (нисходящее, модульное проектирование, структурное программирование).

В связи с этим появились многочисленные реализации языка для разных машинных архитектур и наиболее удачной и популярной оказалась разработка фирмы Borland International для персональных IBM — совместимых ЭВМ. Эта реализация языка получила название Turbo Pascal (Турбо Паскаль) и имеет уже несколько версий.

Turbo Pascal представляет собой систему программирования, включающую в себя текстовый редактор, компилятор, компоновщик, загрузчик, отладчик, файловую систему, системную библиотеку, справочную систему. Все эти компоненты объединены в интегрированную среду с многооконным интерфейсом и развитой системой меню, что обеспечивает высокую производительность труда программиста при создании программ производственного, научного и коммерческого назначения.

Написать программу на языке программирования Pascal, выполняющую решение нелинейного уравнения. Результат работы программы должен выводиться на экран и в файл.

В программе реализовать следующее меню:

1-Ввести данные из файла

2-Ввести данные с клавиатуры

3-Отобразить результат

4-Сохранить результат в файл

0-Выход

Отладить программу на уравнении f(x)=x ² -x-6 с точностью 0,001

2. ВЫБОР И ОПИСАНИЕ МЕТОДОВ РЕШЕНИЯ

отделённым

: метод половинного деления, Ньютона

2.1. МЕТОД ПОЛОВИННОГО ДЕЛЕНИЯ

Пусть дано уравнение f (x ) = 0, где f (х ) – непрерывная функция. Требуется найти корень этого уравнения ξ с точностью до ε, где е – некоторое положительное достаточно малое число.

Будем считать, что корень ξ отделен и находится на отрезке [ а , b ], т. е. имеет место неравенство а ≤ ξ ≤ b . Числа а и b – приближенные значения корня ξ соответственно с недостатком и с избытком. Погрешность этих приближений не превышает длины отрезка b – а . Если b – а ≤ε, то необходимая точность вычислений достигнута, и за приближенное значение корня ξ можно принять либо а , либо b . Но если b – а > ε, то требуемая точность вычислений не достигнута и необходимо сузить интервалов котором находится корень ξ, т. е. подобрать такие числа а и b , чтобы выполнялись неравенства a < ξ < b и . При вычисления следует прекратить и за приближенное значение корня с точностью до ε принять либо а , либо b . Следует отметить, что значение корня будет более точным, когда за приближенное значение корня приняты не концы отрезка а и b , а середина этого отрезка, т.е. . Погрешность в этом случае не превышает величины .

История языков програмирования

... на универсализацию языков была продолжена. Старые языки были модернизированы в универсальные варианты. Примером тому стал FORTRAN 77. Значительным событием в истории языков программирования стало создание в 1971 году языка PASCAL. ... гуру» 2. Ассемблер Первым значительным шагом представляется переход к языку ассемблера (позволим себе ... язык которой приближен к разговорному, Г. Хоппер связывала с тем, ...

Метод проб

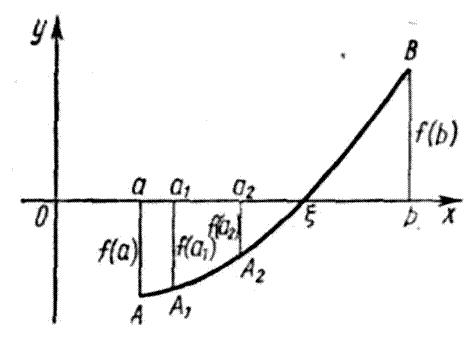
Рис. 2.1

Принцип решения уравнения типа y=f(x) методом проб

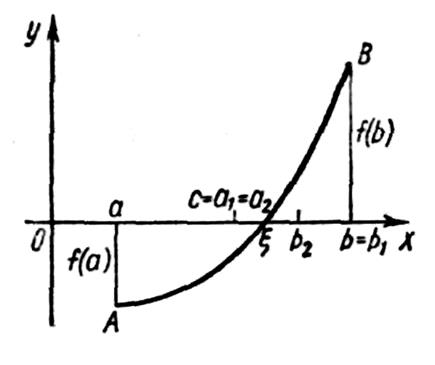
Рис. 2.2

Принцип решения уравнения типа y=f(x) методом половинного деления

На отрезке [ a , b ] выберем произвольным образом точку a₁ , которая разделит его на два отрезка [a, a₁ ] и [a₁ ,b]. Из этих двух отрезков следует выбрать тот, на концах которого функция принимает значения, противоположные по знаку. В нашем примере f (а ) ∙ f (a ₁ ) > 0, f (a ₁ ) ∙ f (b ) < 0; поэтому следует выбрать отрезок [a ₁ ,b ]. Затем на этом суженом отрезке опять произвольным образом возьмем точку а ₂ и найдем знаки произведений f (a ₁ ) ∙ f (a ₂ ) и f (a ₂ ) ∙ f (b ).

Так как f (a ₂ )× f (b ) < 0, то выбираем отрезок [a ₂ , b ]. Этот процесс продолжаем до тех пор, пока длина отрезка, на котором находится корень, не станет меньше ε. Корень ξ получим как среднее арифметическое концов найденного отрезка, причем погрешность корня не превышает ε/2.

метода половинного деления

Пусть корень ξ уравнения f (х ) = 0 отделен и находится на отрезке [a , b ], т.е. f (a ) ∙ f (b ) < 0, причем b – а > ε [здесь f (х) – непрерывная функция]. Как и ранее, возьмем на отрезке [a , b ] промежуточную точку, однако не произвольным образом, а так, чтобы она являлась серединой отрезка [a , b ], т. е. с = (а + b )/2. Тогда отрезок [a , b ] точкой с разделится на два равных отрезка [а , с ] и [с , b ], длина которых равна (b – а )/2 (рис. 2.2).

Приближённые методы решения алгебраического уравнения

... предположениях уравнение (1.1) имеет в точности один корень на интервале (a , b ). 2. Метод дихотомии Этот метод ещё называется методом вилки. Нам необходимо найти корень уравнения (1.1) на отрезке [ a , b ]. Рассмотрим отрезок [x ... Таким образом, разность с 2 -с 1 меньше любого наперёд заданного положительного числа. Это означает, что с 2 -с 1 = 0, т. е.: с 1 =с 2 =с Найденная точка интересна тем, ...

Если f (с ) = 0, то с – точный корень уравнения f (х ) = 0. Если же f (с ) ≠ 0, то из двух образовавшихся отрезков [a , с ] и [с , b ] выберем тот, на концах которого функция f (х) принимает значения противоположных знаков; обозначим его [a _l , b ₁ ]. Затем отрезок [a _l , b ₁ ] также делим пополам и проводим те же рассуждения. Получим отрезок [а ₂ , b ₂ ], длина которого равна (b – а )/2² . Процесс деления отрезка пополам производим до тех пор, когда на каком-то n-м этапе либо середина отрезка будет корнем уравнения (случай, весьма редко встречающийся на практике), либо будет получен отрезок [a _n , b _n ] такой, что b _n – а _n = (b – а)/2ⁿ ≤ ε и а _n ≤ ξ ≤ b _n (число n указывает на количество проведенных делений).

Числа а _n и b _n – корни уравнения f (х ) = 0 с точностью до ε. За приближенное значение корня, как указывалось, выше, следует взять ξ = (a _n + b _n )/2, причем погрешность не превышает (b – а )/2^{n +1} .

2.2. МЕТОД ХОРД

Метод хорд является одним из распространенных методов решения алгебраических и трансцендентных уравнений. В литературе он также встречается под названиями «метода ложного положения» (regulafalsi), «метода линейного интерполирования» и «метода пропорциональных частей».

Пусть дано уравнение f(х) = 0, где f (х) – непрерывная функция, имеющая в интервале [а, b] производные первого и второго порядков. Корень считается отделенным и находится на отрезке [а, b], т.е. f(a)-f (b) < 0.

Идея метода хорд состоит в том, что на достаточно малом промежутке [а, b] дуга кривой у = f (x) заменяется стягивающей ее хордой. В качестве приближенного значения корня принимается точка пересечения хорды с осью Ох.

Ранее мы рассмотрели четыре случая расположения дуги кривой, учитывая значения первой и второй производных.

Рассмотрим случаи, когда первая и вторая производные имеют одинаковые знаки, т. е, f'(х) ∙ f» (х) > 0.

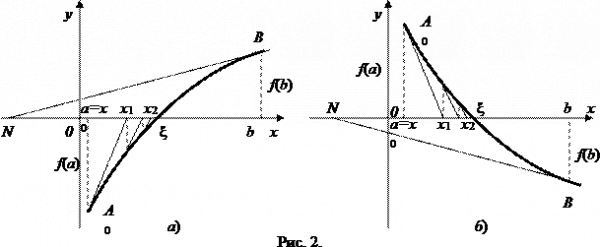
Пусть, например, f(a) < 0, f(b) > 0, f'(х) > 0, f»(х) > 0 (рис. 3.18, а).

График функции проходит через точки А ₀ (a; f(a)), В(b; f(b))- Искомый корень уравнения f(х) = 0 есть абсцисса точки пересечения графика функции у = f(х) с осью Ох. Эта точка нам неизвестна, но вместо нее мы возьмем точку x₁ пересечения хорды А и В с осью Ох. Это и будет приближенное значение корня.

Уравнение хорды, проходящей через точки А ₀ и В, имеет вид

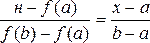
Найдем значение х = х ₁ , для которого у = 0:

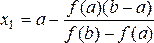
Эта формула носит название формулы метода хорд. Теперь корень ξ находится внутри отрезка [x ₁ , b]. Если значение корня х₁ нас не устраивает, то его можно уточнить, применяя метод хорд к отрезку [х₁ , b].

Рис

Соединим точку А ₁ (x₁ ; f (x₁ ) с точкой В (b; f (b)) и найдем х₂ – точку пересечения хорды А₁ В с осью Ох:

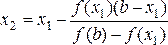
Продолжая этот процесс, находим

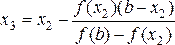
и вообще

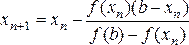
Процесс продолжается до тех пор, пока мы не получим приближенный корень с заданной степенью точности.

По приведенным выше формулам вычисляются корни и для случая, когда f(а) > 0, f(b) < 0, f'(x) < 0, f»(x) < 0 (рис. 3.18, б).

Теперь рассмотрим случаи, когда первая и вторая производные имею разные знаки, т.е. f'(x) ∙ f'(x) < 0.

Пусть, например, f(a) > 0, f(b) < 0, f'(х) < 0, f»(х) > 0 (рис. 3.19, а).

Соединим точки A (a; f (а)) и В ₀ (b; f (b)) и запишем уравнение хорды, проходящей через А и B₀ :

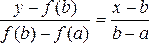
Найдем х ₁ , как точку пересечения хорды с осью Ох, полагая у = 0:

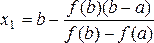
Корень ξ теперь заключен внутри отрезка [a, x ₁ ]. Применяя меч од хорд к отрезку [а, x₁ ], получим

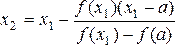
и вообще

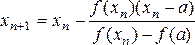
По этим же формулам находится приближенное значение корня и для случая, когда f(а) < 0, f(b)>0, f'(х) > 0, f»(х) < 0 (рис. 3.19, б).

Итак, если f'(х) ∙ f»(х) > 0, то приближенный корень вычисляется по формулам (1) и (2); если же f(х) ∙ f»(x) < 0, то – по формулам (3) и (4).

Однако выбор тех или иных формул можно осуществить, пользуясь простым правилом: неподвижным концом отрезка является тот, для которого знак функции совпадает со знаком второй производной.

Если f(b) ∙ f» (х) > 0, то неподвижен конец b, а все приближения к корню ξ лежат со стороны конца а [формулы (1) и (2)]. Если f(а)×f»(x) > 0. то неподвижен конец а, а все приближения к корню ξ лежат со стороны конца b [формулы (3) и (4).

2.3. МЕТОД НЬЮТОНА (МЕТОД КАСАТЕЛЬНЫХ)

Пусть корень уравнения f (х) = 0 отделен на отрезке [а , b ], причем f ‘(х ) и f «(x ) непрерывны и сохраняют постоянные знаки на всем отрезке [а, b].

метода Ньютона

Первый случай

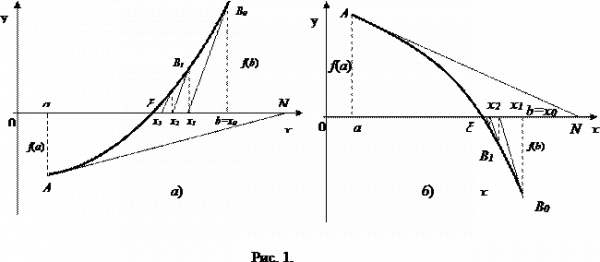
Полагая у = 0, х = х1, получим

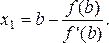(1)

Теперь корень уравнения находится на отрезке [ а , х ₁ ]. Применяя снова метод Ньютона, проведем касательную к кривой в точке B ₁ (x ₁ ; f (x ₁ )) и полечим

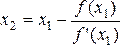
и вообще

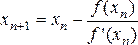(2)

Получаем последовательность приближенных значений x ₁ , х ₂ , …, x _n , …, каждый последующий член которой ближе к корню ξ, чем предыдущий. Однако все х _n , остаются больше истинного корня ξ, т.е. х _n – приближенное значение корня ξ с избытком.

Второй случай

Полагая у = 0, x = x1 находим

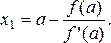(3)

Корень ξ находится теперь на отрезке [ х ₁ , b ]. Применяя снова метод Ньютона, проведем касательную в точке A ₁ (x ₁ ; f (x ₁ )) и получим

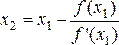
и вообще

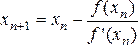(4)

Получаем последовательность приближенных значений х ₁ , х ₂ , … ,х _n ,…, каждый последующий член которой ближе к истинному корню ξ, чем предыдущий, т.е. х _n – приближенное значение корня ξ с недостатком.

Сравнивая эти формулы с ранее выведенными, замечаем, что они отличаются друг от друга только выбором начального приближения: в первом случае за х ₀ принимался конец b отрезка, во втором – конец а .

При выборе начального приближения корня необходимо руководствоваться следующим правилом: за исходную точку следует выбирать тот конец отрезка [ а , b ], в котором знак функции совпадает со знаком второй производной. В первом случае f (b ) ∙ f »(х ) > 0 и начальная точка b = x₀ , во втором f (a ) ∙ f «(x ) > 0 и в качестве начального приближения берем а = х ₀ .

Соответствие между переменными, используемыми в блок-схеме и в программном коде главной программы приведено в Таблице 1.

Соответствие между переменными, используемыми в блок-схеме и в программном коде процедуры Save приведено в Таблице 2.

Таблица 1

Соответствие между переменными, используемыми в блок-схеме и в программном коде главной программы

Обозначения принятые при описании задачи	Обозначения в программе	Наименование
а	а	Левая граница интервала
b	b	Правая граница интервала
е	е	Точность
х	х	Корень
Key	Key	Содержит символ нажатой клавиши

Таблица 2

Соответствие между переменными, принятыми при описании задачи и в процедуре Save

Обозначения принятые при описании задачи	Обозначения в программе	Наименование
f	f	Файловая переменная
S	S	Название файла

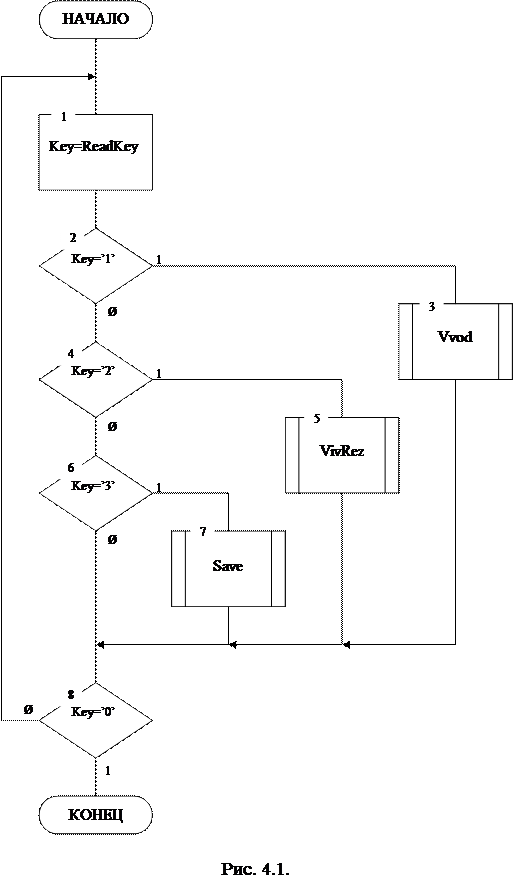
Структурная схема главной программы приведена на рис. 4.1.

Блок 1: ввод клавиши выбора пункта меню;

• Блок 2: если выполняется условие Key=’1’ то выполнить блок, 3 иначе выполнить блок 4;
• Блок 3: обращение к процедуре ввода исходных данных Vvod;
• Блок 4: если выполняется условие Key=’2’ то выполнить блок 5, иначе выполнить блок 6;
• Блок 5: обращение к процедуре поиска корня и вывода его на экранVivRez;
• Блок 6: если выполняется условие Key=’3’ то выполнить блок 7, иначе выполнить блок 8;
• Блок 7: обращение к процедуре поиска корня и сохранения его в файл;
• Блок 8: если выполняется условие Key=’0’ то выйти из программы, иначе вернуться к блоку 1.

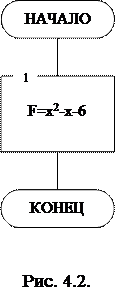
Структурная схема подпрограммы функции f изображена на Рис. 4.2.

Блок 1: присваивание заголовку функции заданного варианта.

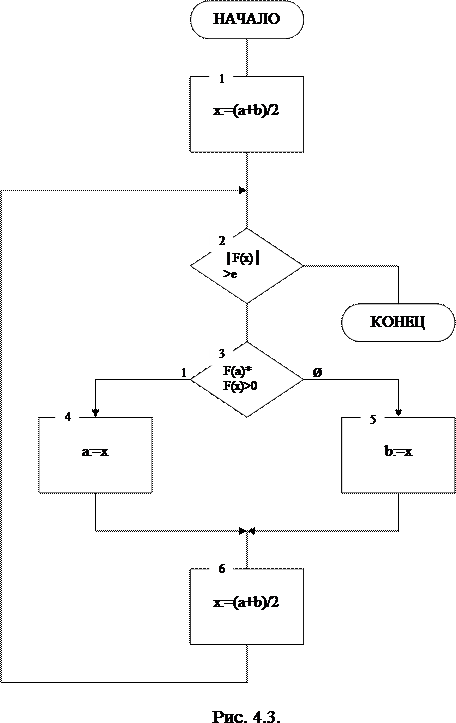
Структурная схема подпрограммы процедуры PolDelизображена на Рис. 4.3.

Блок 1: вычисление начального значения х;

• Блок 2: если значение функции в точке х отстоит от 0 на величину превышающую заданную точность е то выполнить цикл уточнения – перейти к блоку 3, иначе выйти из подпрограммы;
• Блок 3: если функция в точке а и в точке х имеет одинаковый знак то выполнить блок 4, иначе выполнить блок 5;
• Блок 4: левая граница перемещается в точку х;
• Блок 5: правая граница перемещается в точку х;
• Блок 6: вычисление нового значения х.

Структурная схема подпрограммы процедуры Vvodизображена на Рис. 4.4.

Блок 1: вывод запроса на ввод левой границы интервала;

• Блок 2: ввод а – левой границы интервала;
• Блок 3: вывод запроса на ввод правой границы интервала;
• Блок 4: ввод b– правой границы интервала;
• Блок 5: вывод запроса на ввод точности вычисления корня уравнения;
• Блок 6: ввод е – точности вычисления корня уравнения.

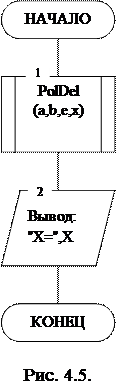
Структурная схема подпрограммы процедуры Vivrezизображена на Рис. 4.5.

Блок 1: обращение к процедуре вычисления корня уравнения PolDel;

• Блок 2: вывод найденного корня.

Структурная схема подпрограммы процедуры Saveизображена на Рис. 4.6.

Блок 1: вывод запроса названия файла;

• Блок 2: ввод названия файла;
• Блок 3: обращение к процедуре подключения файла с введённым именем;
• Блок 4: обращение к процедуре открытия файла для записи;
• Блок 5: обращение к процедуре вычисления корня уравнения PolDel;
• Блок 6: вывод в файл полученного значения корня;
• Блок 7: обращение к процедуре закрытия файла.

Листинг программы находится в приложении А.

Для контрольного примера найдём значение корня на интервале от 0 до 5. Найдём этот корень графически с использованием программы MicrosoftExcel (см. табл 6.1., рис. 6.1).

Найдём этот корень при помощи программы (см. рис 6.2.-6.3).

Полученное при помощи программы значение корня соответствует расчётному.

Таблица. 6.1

Расчетные точки графика функции f(x)=x ² -x-6, полученные при помощи программы MicrosoftExcel

x	y
0	-6
1	-6
2	-4
3	0
4	6
5	14

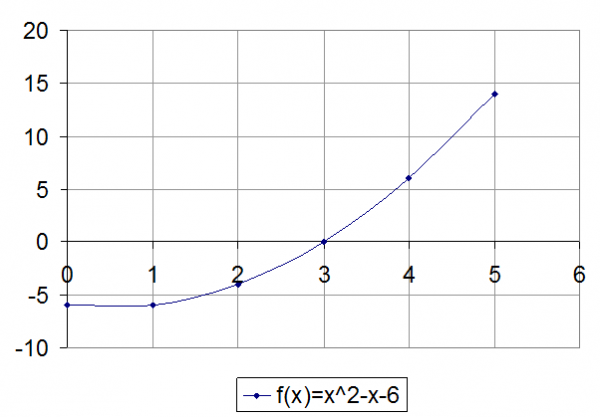
Рис. 6.1.

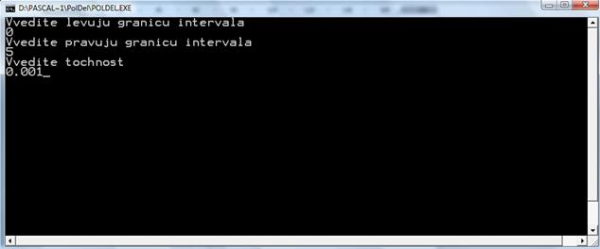
Рис. 6.1.

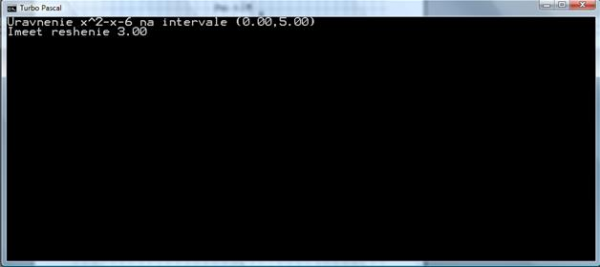
Рис. 6.2.

Для работы с программой нужно запустить программу POLDEL.EXE, находящийся на дискете в приложении D, занимающий 20 кБ.

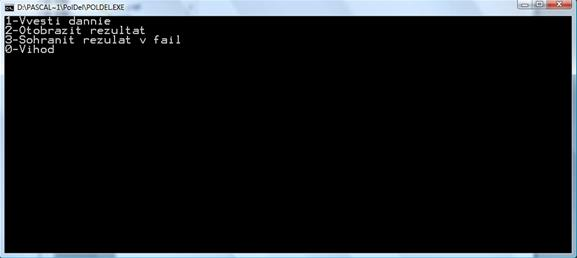
После запуска программы на экране появляется меню программы в котором содержатся следующие пункты (см. Прил. Б).

1) 1-Ввести данные

2) 2-Отобразить результат

3) 3-Сохранить результат в файл

4) 0-Выход

ввода исходных данных

просмотра результата вычисления

сохранения результата

выхода из программы

В данной курсовой работе была разработана программа, решающая нелинейное уравнение. Для его решения был выбран метод половинного деления.

1. Кетков Ю.Л., Кетков А.Ю. Практика программирования: Бейсик, Си, Паскаль. Самоучитель. – СПб.: БХВ-Петербург, 2001. 408 с.: ил.

2. Любиев О.Н., Филиппенко Л.Н., Филиппенко Г.Г. Методические указания к выполнению курсовой работы по дисциплинам «Программирование на ЯВУ, Информатика», Новочеркасск, ЮРГТУ, 2003г. – 256 с.

3. Фаронов В.В. «Турбо Паскаль 7.0» Начальный курс. Учебное пособие. Издание 7-е, переработанное. – М.: «Нлидж», издатель Молчалева С.В., 2001.-576 с. с ил.

4. Абрамов В.Г., Трифонов Н.П. Введение в язык Паскаль. – М. :Наука, 1988.-320 с.

ЛИСТИНГ ПРОГРАМЫ

Program PolD;

Uses

CRT;

Var

a,b,e,x:real;

• Function F(var x:real):real;

begin

f:=sqr(x)-x-6;

• end;

{================================}

Procedure PolDel(a,b,e:real; var x:real);

begin

x:=(a+b)/2;

• while abs(F(x))>e do

begin

if F(a)*F(x)>0 then a:=x

else b:=x;

• x:=(a+b)/2;
• end;
• end;

{===============================}

Procedure Vvod;

begin

Clrscr;

• Writeln(‘Vvedite levuju granicu intervala’);
• Readln(a);
• Writeln(‘Vvedite pravuju granicu intervala’);
• ReadLn(b);
• Writeln(‘Vvedite tochnost’);
• ReadLn(e);
• end;

{===============================}

Procedure Vivrez;

begin

Clrscr;

• PolDel(a,b,e,x);

• Writeln(‘Uravnenie x^2-x-6 na intervale (‘,a:0:2,’,’,b:0:2,’)’);

• Writeln(‘Imeet reshenie ‘,x:0:2);

ReadKey

end;

{===============================}

Procedure Save;

var

f:text;

• S:string;

begin

Clrscr;

• Writeln(‘Vvedite nazvanie faila’);
• ReadLn(S);
• Assign(f,s);

{$I-}

ReWrite(f);

{$I+}

PolDel(a,b,e,x);

• Writeln(f,’Uravnenie x^2-x-6 na intervale (‘,a:0:2,’,’,b:0:2,’)’);

• Writeln(f,’Imeet reshenie ‘,x:0:2);

Close(f)

end;

{===============================}

var

Key:Char;

Begin

repeat

Clrscr;

• Writeln(‘1-Vvesti dannie’);
• Writeln(‘2-Otobrazit rezultat’);
• Writeln(‘3-Sohranit rezulat v fail’);
• Writeln(‘0-Vihod’);
• Key:=ReadKey;

Case Key of

‘1’:Vvod;

• ‘2’:VivRez;
• ‘3’:Save;
• end;
• until Key=’0′;
• end.

МЕНЮ ПРОГРАММЫ

ДИСКЕТА С ПРОГРАММОЙ