Устойчивость сжатых стержней. Прочность при циклически изменяющихся нагрузках (напряжениях)

метки: Критический, Предельный, Нагрузка, Стержень, Прочность, Материал, Предел, Элемент

БЕЛОРУССКИЙ ГОСУДРАСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ

Кафедра инженерной графики

РЕФЕРАТ

На тему:

«Устойчивость сжатых стержней. Прочность при циклически изменяющихся нагрузках (напряжениях)»

МИНСК, 2008

Устойчивость равновесия сжатого стержня

В нагруженных телах при любом деформированном состоянии имеет место равновесие между внешними и внутренними силами. Деформированное состояние характеризуется формой тела, формой равновесия. Под устойчивостью понимают свойство тела сохранять свою первоначальную форму равновесия.

Рассмотрим формы равновесия при сжатии стержней. При сжатии короткого жесткого стержня (рис. 1, а) его рассчитывают на прочность и жесткость по формулам для осевого сжатия (подразд. 5.4).

При сжатии стержня, имеющего достаточно большую длину по сравнению с поперечными размерами, возможно следующее. Пока сжимающая сила F мала и ось стержня (рис. 1, б, г) строго прямолинейна, стержень находится в состоянии устойчивого равновесия. При величине сжимающей силы, равной некоторому критическому значению F_cr ось стержня искривляется (рис. 1, в, д).

В этом случае начальная (расчетная) прямолинейная форма равновесия становится неустойчивой. Критической силой F_cr называется наименьшее значение сжимающей силы, при котором ось сжатого стержня теряет прямолинейность.

По определению Эйлера, критической силой называется сжимающая сила, требуемая для самого малого наклонения колонны.

д

г

в

б

а

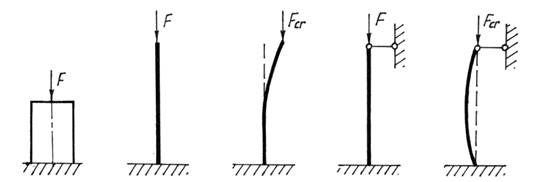
Рис. 1

Понятие устойчивости не нужно смешивать с понятием прочности, каждое из них имеет самостоятельное значение. Например, сжатый стержень при действии силы, большей критической, изогнется, но деформации его будут упругими и он после снятия нагрузки восстановит свою первоначальную форму. Потеря устойчивости в этом случае не связана с потерей прочности; но в иных случаях потеря устойчивости, изменяя формы элемента, может привести к разрушению или невозможности элемента выполнять свои функции.

устойчивость

F _adm = F_cr /n_S , (1)

n _S

Потеря устойчивости была причиной многих аварий и катастроф; она возможна при кручении, изгибе и сложных деформациях.

Определение критической силы, задача Эйлера

F _cr

d ² y/dx² = М_и /EI. (2)

а

б

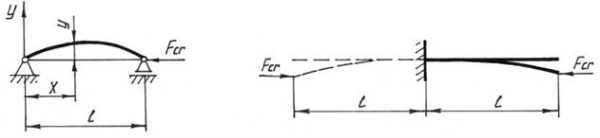
Рис. 2

Изгиб происходит в плоскости минимальной жесткости, т.е. поперечные сечения будут поворачиваться вокруг той оси, относительно которой момент инерции I имеет минимальное значение. Изгибающий момент по абсолютной величине в любом сечении равен

М _и = F_cr ·y, (3)

где у – прогиб поперечного сечения. Так как прогиб у и вторая производная от него d² y/dx² при любом направлении оси у всегда имеют противоположные знаки, уравнение (5.92) выразим как

d ² y/dx² = (–F_cr ·y)/(EI).

(4)

Обозначая

k ² = F_cr /(EI), (5)

представим уравнение (5.94) в виде y» + k ² y = 0. Это линейное дифференциальное уравнение второго порядка. Его общее решение имеет вид

y = C sin kx + D cos kx. (6)

Для определения постоянных интегрирования С и D используем известные граничные условия, а именно, условия крепления на концах стержня: при х = 0 и при х = ℓ прогиб отсутствует, т.е. у = 0.

Подставляя в уравнение (6) данные первого условия, определим, что D = 0, а стержень изгибается по синусоиде у = Csinkx. Из второго граничного условия найдем С sinkℓ = 0. Полученное соотношение справедливо, если С = 0 или sinkℓ = 0. Если считать С = 0, то при D = 0 прогиб (5.96) во всех поперечных сечениях по длине стержня при любых значениях х отсутствует, что противоречит исходной предпосылке. Выражение sinkℓ = 0 справедливо, когда kℓ = nπ, где n – произвольное целое число (n = 0, 1, 2, …).

Подставляя значение k = (πn)/ℓ в выражение (5), получим что

F _cr = k² EI = (π² n² EI)/ℓ² . (7)

наименьшее

F _cr = (π² EI)/ℓ² . (8)

Используя особенности упругой линии, можно распространить полученное решение на другие случаи закрепления стержня. Так, если стержень на одном конце жестко защемлен, а на другом – свободен (рис. 2, б), то упругую линию стержня легко привести путем зеркального отображения относительно заделки к упругой линии шарнирно закрепленного стержня (рис. 2, а).

Очевидно, критическая сила стержня с таким закреплением длиной ℓ будет равна критической силе шарнирно закрепленного стержня длиной 2ℓ.

Общее выражение критической силы для сжатого стержня в обобщенном виде с учетом его типа крепления примет вид

F _cr = (π² EI)/(υℓ)² (9)

υ – коэффициент приведения длины

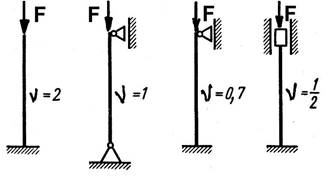
Рис. 3

Прочность при циклически изменяющихся нагрузках (напряжениях).

Понятие об усталости материалов

Работа механизмов характеризуется определенностью движений и нагружений звеньев, повторяемостью через определенные промежутки времени (периоды) этих движений. Значительная часть элементов механизмов (валы, зубья зубчатых колес и т.д.) испытывает в процессе эксплуатации периодические изменяющиеся по величине и знаку механические нагрузки. Замечено, что при таком нагружении разрушение деталей происходит при напряжениях, значительно меньших предельных напряжений (предела текучести) при статическом нагружении. Характер разрушения материалов при переменных повторяющихся нагрузках существенно отличается от вида разрушения при статическом нагружении. Разрушение начинается с образования на поверхности элементов микротрещин, которые развиваются вглубь материала, уменьшая площадь поперечного сечения детали. Разрушение происходит внезапно при достаточном ослаблении сечения и на поверхности разрушения видны две характерные зоны: зона постепенного развития трещины и зона внезапного разрушения. Процесс постепенного накопления повреждений под действием повторяющихся знакопеременных нагрузок, приводящий к внешне непроявляющемуся изменению свойств (электропроводимость, микротвердость и др.) материала, к зарождению и развитию трещин, и, наконец, к разрушению элемента, называют усталостью . Усталостное разрушение – длительный процесс, связанный с многократным нагружением. Свойство материала (изделия) сопротивляться усталости называют выносливостью, или усталостной прочностью .

Совокупность последовательных значений напряжений (нагрузок) за один период называют циклом напряжений (нагрузок).

Замечено, что сопротивление усталости зависит от значений наибольшего и наименьшего напряжений цикла, их отношения и практически не зависит от закона изменения (синусоидальный, треугольный, трапецеидальный и др.) напряжений внутри цикла. Будем считать, что напряжения меняются во времени по закону, близкому к синусоиде (рис. 4).

Цикл напряжений характеризуется следующими величинами: максимальным σ _max и минимальным σ _min напряжениями, т.е. наибольшим и наименьшим по алгебраическому значению (с учетом знаков) напряжениями; средним напряжением σ _m , равным алгебраической полусумме σ _max и σ _min (σ_m = (σ_max + σ_min )/2); амплитудой цикла напряжений σ _a , равной полуразности σ _max и σ _min (σ_a = (σ_max – σ_min )/2); коэффициентом асимметрии цикла R , равным отношению минимального напряжения к максимальному, т.е. R = σ_min / σ_max . На рис. 4, а показан асимметричный цикл напряжений, когда |σ_max | ≠ |σ_min |. Наиболее часто на практике встречаются симметричный и отнулевой циклы напряжений. Для симметричного цикла имеем σ_max = σ; σ_min = –σ; σ_a = σ; σ_m = 0; R = –1; а для отнулевого (пульсационного): σ_max = σ; σ_min = 0; σ_a = σ_m = σ/2; R = 0, где σ – максимальное по величине напряжение цикла. Постоянное статическое напряжение (рис. 4, г) можно рассматривать как частный случай переменного с параметрами σ_max = σ_min = σ_m = σ; σ_a = 0; R = + 1. Наиболее опасны симметричные циклы нагружения.

Все переменные циклы напряжений, кроме симметричного, называют асимметричными. Циклы с одинаковыми коэффициентами асимметрии R называют подобными . При действии переменных касательных напряжений все приведенные выше характеристики и соотношения остаются в силе с заменой σ на τ .

г

в

б

а

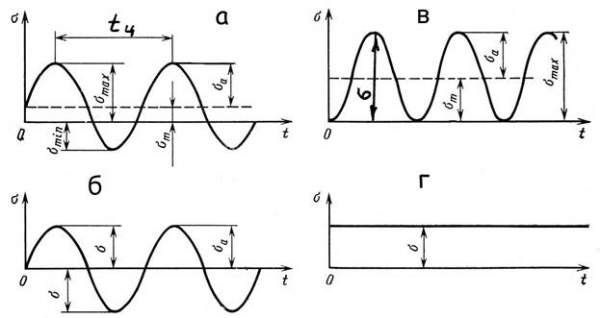
Рис. 4

Характеристики усталостной прочности материалов. Предел выносливости

предел выносливости σ

материалов предел выносливости 1">

Рис. 5

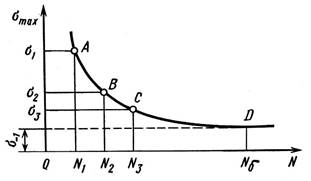
Рис. 6

кривой усталости

σ ₂

В литературе предлагаются десятки уравнений, описывающих кривые усталости разных материалов, образцов. В инженерных расчетах чаще всего используют степенное уравнение кривой усталости

σ ^m N = const, (10)

где N – число циклов до разрушения при максимальном напряжении σ цикла; m – показатель степени, зависящий от материала, параметров образца, для металлов m = 5 … 10.

σ _–1

, (11)

или рассчитать возможное число циклов N нагружения при задаваемом, большем предела выносливости, максимальном напряжении σ_{–1 N} цикла

N = N _σ (σ_–1 /σ_{–1 N} )^m , (12)

σ _–1

Определение характеристик усталостной прочности материалов путем испытаний на усталость трудоемкий и дорогостоящий процесс из-за длительности и значительного разброса результатов испытаний. Ищут эмпирические зависимости приближенной оценки значений предела выносливости от величины механических свойств материала при статическом нагружении. Так, величина предела выносливости при изгибе с симметричным циклом нагружения для углеродистой стали σ _–1 = (0,4 … 0,45)σ_ut ; для цветных металлов σ_–1 = = (0,24 … 0,5)σ_ut , где σ _ut – предел прочности материала при растяжении.

Влияние коэффициента асимметрии цикла на усталостную прочность. Диаграмма предельных циклов напряжений

σ _–1

σ _max = σ_m + σ_a . (13)

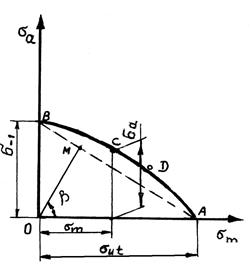
Рис. 7

Диаграмму предельных циклов напряжений строят в координатах σ _m – σ_a (рис. 7).

Точка А диаграммы соответствует пределу прочности материала σ _ut при статическом растяжении, точка В – пределу выносливости σ_–1 при симметричном цикле. Промежуточные точки диаграммы можно определить, используя зависимость (13) при обработке результатов испытаний на оборудовании, позволяющем создавать асимметричные циклы нагружения. Например, задавшись средним напряжением σ _m , устанавливаем в результате серии испытаний значение предельной амплитуды σ _a , соответствующей базовому числу циклов нагружения. Результат представляют на диаграмме точкой С . Продолжая испытания с разными величинами σ _m , получают множество точек, через которые должна проходить кривая искомой диаграммы. Площадь диаграммы, ограниченная кривой А D СВ и осями координат, определяет область безопасных с точки зрения разрушения циклов нагружения. Полученная путем сложных длительных испытаний кривая может быть заменена прямой АВ . Рабочая область безопасного нагружения сократится, но при этом получаем погрешность, увеличивающую запас прочности рассчитываемых элементов. Упрощенную диаграмму легко построить, для этого достаточно знать только значения предела прочности материала при растяжении σ _ut и предела выносливости σ_–1 при симметричном цикле нагружения. Имея приближенную диаграмму предельных циклов напряжений (см. рис. 7), можно определить предел выносливости σ _R при любом цикле нагружения. Если известен коэффициент асимметрии R цикла нагружений, величину σ _R определяют по диаграмме в следующей последовательности.

Произвольный луч ОМ диаграммы является геометрическим местом точек, характеризующих циклы с одинаковым коэффициентом асимметрии R . Угол наклона β луча к оси σ _m связан с величиной R

tg β = σ _a /σ_m = (1 – R)/(1+R).

(14)

Для определения по диаграмме искомого предела выносливости при известном R проводим под углом β = arctg [(1 – R)/(1 + R)] к оси абсцисс луч из точки О до пересечения в точке М с прямой АВ . Предел выносливости σ _R находим , используя выражение (13) как сумму координат точки М (σ_R = = σ_m + σ_a ).

Для отнулевого цикла можно принять σ ₀ ≈ (1,45 … 1,65)σ_–1 .

Факторы, влияющие на предел выносливости

На выносливость, сопротивление усталости элементов влияют ряд факторов, которые не учитываются в расчетах на прочность при статических нагрузках. В частности, на предел выносливости значительно влияют не только свойства материала, но и концентрация напряжений, размеры поперечных сечений элементов, состояние поверхности и другие факторы. Рассмотрим их влияние более подробно.

Влияние концентрации напряжений, Влияние размеров деталей, Влияние состояния поверхности

коэффициента влияния поверхностного упрочнения К

С учетом совместного влияния перечисленных факторов предел выносливости элемента σ _Rd меньше предела выносливости σ_R стандартных образцов. Его определяют по формуле

σ _Rd = (σ_R ·K_d ·K_F ·K_v )/K_σ (15)

При известном максимальном напряжении σ _max цикла запас прочности при переменных напряжениях равен

n = σ _Rd /σ_max . (16)

Обычно коэффициент запаса усталостной прочности находится в пределах 1,3 … 5. При расчетах на прочность по касательным переменным напряжениям все приведенные выше рассуждения имеют силу, естественно, обозначения σ в соответствующих выражениях необходимо заменить на τ .

ЛИТЕРАТУРА

[Электронный ресурс]//URL: https://inzhpro.ru/referat/predelnaya-kriticheskaya-nagruzka/

1. Красковский Е.Я., Дружинин Ю.А., Филатова Е.М. Расчет и конструирование механизмов приборов и вычислительных систем: Учебное пособие. М.: – Высш. шк., 2001. – 480 с.

2. Сурин В.М. Техническая механика: Учебное пособие. – Мн.: БГУИР, 2004. – 292 с.

3. Ванторин В.Д. Механизмы приборных и вычислительных систем: Учебное пособие. – М.: Высш. шк., 1999. – 415 с.