–это кроссплатформенная система компьютерной алгебры (СКА), обладающая сходным с Matlab синтаксисом встроенного языка. Разработка системы Scilab ведется сотрудниками французского Национального института информатики и автоматизации (INRIA – InstitutNationaldeRechercheenInformatiqueetAutomatique) с 80-х годов прошлого века.
Изначально это был коммерческий проект под названием Blaise, а затем Basile. С 2003 года продукт получил новое имя Scilab и стал бесплатным. В настоящее время он распространяется по свободной лицензии CeCILL.
Сама система Scilab, как и Matlab, предназначена прежде всего для численных расчетов и работы с матрицами. Кроме того, она обладает развитыми средствами программирования (включая отладчик скриптов), так что ее в какой-то мере можно рассматривать как систему разработки высокотехнологичных приложений.
1 Программирование в Scilab
В Scilab встроен мощный язык программирования с поддержкой объектов.
Работа в Scilab может осуществляться не только в режиме командной строки, но и в так называемом программном режиме.
Для создания программы (программу в Scilab иногда называют сценарием) необходимо:
1. Вызвать команду Editor из меню (см. рис. 1).
2. В окне редактора Scipad набрать текст программы.
3. Сохранить текст программы с помощью команды File – Save в виде файла с расширением sce , например, file.sce .
4. После этого программу можно будет вызвать, набрав в командной строке exec, например, exec(«file.sce»).
Другие способы вызова — воспользоваться командой меню File – Exec. . . или, находясь в окне Scipad, выполнить команду Execute – Load into Scilab (Ctrl+L ).
Программный режим достаточно удобен, так как он позволяет сохранить разработанный вычислительный алгоритм в виде файла и повторять его при других исходных данных в других сессиях. Кроме обращений к функциям и операторов присваивания, в программных файлах могут использоваться операторы языка программирования Scilab (язык программирования Scilab будем называть sci-языком).
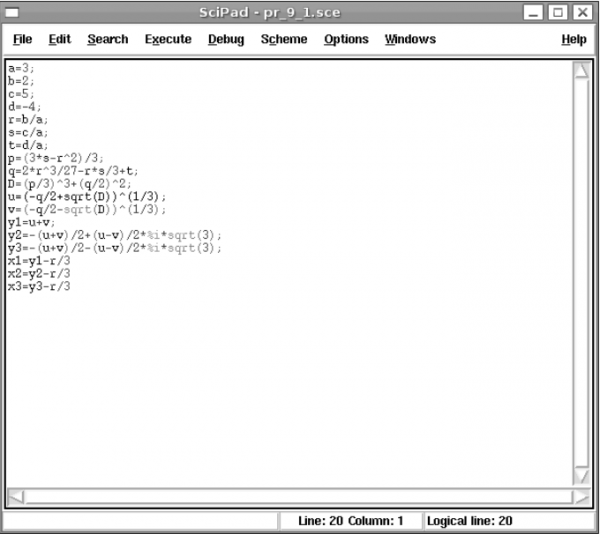
Рис. 1 Окно Scipad с программой решения кубического уравнения
2 Основные операторы sci-языка
2.1 Функции ввода-вывода в Scilab
Для организации простейшего ввода в Scilab можно воспользоваться функциями
Создание проекта для тестирования знаний студентов по языку программирования ...
... разработки приложений был выбран продукт фирмы Borland Delphi 7.0, что обусловлено очень богатыми возможности среды программирования (работа ... какие-либо настройки запрашиваются во время работы программы в виде отдельной формы, а ... новую информацию. Анализ результатов проверки данных тестов позволит диагностировать и психофизиологическую личность ... следует выбрать пункт меню File -> New -> Frame, либо ...
x=input(’title’);
или
x=x_dialog(’title’, ’stroka’);
— Функция input выводит в командной строке Scilab подсказку title и ждет, пока пользователь введет значение, которое в качестве результата возвращается в переменную х. Функция x_dialog выводит на экран диалоговое окно с именем title, после чего пользователь может щелкнуть OK, и тогда stroka вернется в качестве результата в переменную x, либо ввести
новое значение вместо stroka, которое и вернется в качестве результата в переменную x. На рисунке 2 представлено диалоговое окно, которое формируется строкой x=x_dialog(’Input X’,’5’).
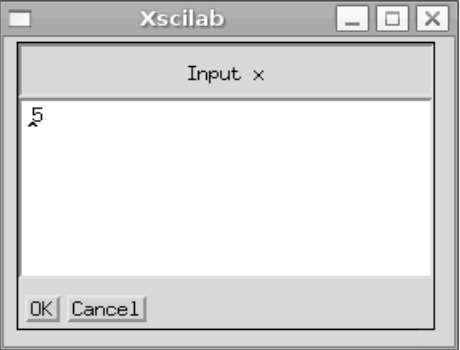
Рис. 2 Окно ввода
Функция input преобразовывает введенное значение к числовому типу данных, а функция x_dialog возвращает строковое значение. Поэтому при использовании функции x_dialog для ввода числовых значений возвращаемую ею строку следует преобразовать в число с помощью функции evstr. Можно предложить следующую форму использования функции x_dialog для ввода числовых значений:
- x=evstr(x_dialog(’title’,’stroka’));
Для вывода в текстовом режиме можно использовать функцию disp следующей структуры:
disp(b)
Здесь b — имя переменной или заключенный в кавычки текст.
2.2 Оператор присваивания
Оператор присваивания имеет следующую структуру
a=b
здесь a — имя переменной или элемента массива, b — значение или выражение.
В результате выполнения оператора присваивания переменной a присваивается значение выражения b.
2.3 Условный оператор
Одним из основных операторов, реализующих ветвление в большинстве языков программирования, является условный оператор if. Существует обычная и расширенная формы оператора if в Scilab. Обычный if имеет вид
if условие
операторы1
else
операторы2
end
Здесь условие — логическое выражение, операторы1, операторы2 — операторы языка Scilab или встроенные функции. Оператор if работает по следующему алгоритму: если условие истинно, то выполняются операторы1, если ложно — операторы2.
В Scilab для построения логических выражений могут использоваться условные операторы: &, and (логическое и), |, or (логическое или), ˜, not (логическое отрицание) и операторы отношения: (больше), == (равно), ˜=, (не равно), = (больше или равно).
Зачастую при решении практических задач недостаточно выбора выполнения или невыполнения одного условия. В этом случае можно, конечно, по ветке else написать новый оператор if, но лучше воспользоваться расширенной формой оператора if.
if условие1
операторы1
else
if условие2
операторы2
else
if условие 3
операторы3
Else
if условие n
операторы n
else
операторы
end
В этом случае оператор if работает так: если условие1 истинно, то выполняются операторы1, иначе проверяется условие2, если оно истинно, то выполняются операторы2, иначе проверяется условие3 и т. д. Если ни одно из условий по веткам else и elseif не выполняется, то выполняются операторы по ветке else.
Приближённые методы решения алгебраического уравнения
... где бы уравнение имело ровно один корень: на концах промежутков имело значения разных знаков. Там где данное условие не выполняется, те промежутки ... с 2 -с 1 меньше любого наперёд заданного положительного числа. Это означает, что с 2 -с 1 = 0, т. е.: с 1 =с 2 =с ... меньше 2Е . Тогда середина последнего отрезка даст значение корня с требуемой точностью. Дихотомия проста и очень надёжна. К простому ...
Задача 1.
В качестве примера программирования разветвляющегося процесса рассмотрим решение биквадратного уравнения ax4 + bx2 + c = 0.
Для решения биквадратного уравнения необходимо заменой y = x^2 привести его к квадратному и решить это уравнение. После этого для нахождения корней биквадратного уравнения необходимо будет извлечь корни из найденных значений y. Входными данными этой задачи являются коэффициенты биквадратного уравнения a, b, c. Выходными данными являются корни уравнения x1, x2, x3, x4 или сообщение о том, что действительных корней нет.
Алгоритм состоит из следующих этапов:
1. Ввод коэффициентов уравнения a, b и c;
2. Вычисление дискриминанта уравнения d;
3. Если d
4. Если y1
5. Если y1 0 и y2 0, то вычисляются четыре корня по формулам ±√y1, ±√y2 и выводятся значения корней.
6. Если условия 4) и 5) не выполняются, то необходимо проверить знак y1.
7. Если y1 неотрицательно, то вычисляются два корня по формуле ±√y1, иначе оба корня вычисляются по формуле ±√y2.
Программа решения биквадратного уравнения на sci-языке приведена на рисунках3-4, ее вызов и результаты — на рисунке 5.

Рис. 3 Программа решения биквадратного уравнения

Рис. 4 Программа решения биквадратного уравнения


Рис. 5 Результат выполнения программы
2.4 Оператор альтернативного выбора
Еще одним способом организации разветвлений является оператор альтернативного выбора select следующей структуры:
select параметр
case значение1 then операторы1
case значение2 then операторы2
else операторы
end
Оператор select работает следующим образом: если значение параметра равно значениию1, то выполняются операторы1, иначе, если параметр равен значениию2, то выполняются операторы2. В противном случае, если значение параметра совпадает со значением3, то выполняются операторы3 и т. д. Если значение параметра не совпадает ни с одним из значений в группах case, то выполняются операторы, которые идут после служебного слова else.
Конечно, любой алгоритм можно запрограммировать без использования select, используя только if, но использование оператора альтернативного выбора select делает программу более компактной.
Основные характеристики и параметры надёжности
... различными функциями и числовыми параметрами. Правильный выбор количественных показателей надежности ЭВМ позволяет объективно сравнивать технические ... постепенного изменения параметров элементов до тех пор, пока значение одного из параметров не выйдет ... оператор, обслуживающий ЭВМ, должен отрегулировать или заменить отказавший элемент. Самоустраняющиеся отказы исчезают без вмешательства оператора ...
Рассмотрим использование оператора select на примере решения следующей задачи.
Задача 2
Вывести на печать название дня недели, соответствующее заданному числу D, при условии, что в месяце 31 день и 1-е число — понедельник.
Для решения задачи воспользуемся условием, что 1-е число — понедельник. Если в результате остаток от деления заданного числа D на семь будет равен единице, то это понедельник, двойке — вторник, тройке — среда и так далее. Вычислить остаток от деления числа x на k можно по формуле x − int(x/k) ∗ x. Следовательно, при построении алгоритма необходимо использовать семь условных операторов.
Решение задачи станет значительно проще, если при написании программы воспользоваться оператором варианта (см. рис. 6).
Вызов программы представлен на рис. 7.

Рис. 6 Решение задачи 2

Рис. 7 Вызов функции для решения задачи 2
Рассмотрим операторы цикла в Scilab. В sci-языке есть два вида цикла: оператор цикла с предусловием while и оператор for.
2.5 Оператор while
Оператор цикла while имеет вид
while условие
операторы
end
Здесь условие — логическое выражение; операторы будут выполняться циклически, пока логическое условие истинно.
Оператор цикла while обладает значительной гибкостью, но не слишком удобен для организации «строгих» циклов, которые должны быть выполнены заданное число раз. Оператор цикла for используется именно в этих случаях.
2.6 Оператор for
Оператор цикла for имеет вид
for x=xn:hx:xk
операторы
end
Здесь x — имя скалярной переменной — параметра цикла, xn — начальное значение параметра цикла, xk — конечное значение параметра цикла, hx — шаг цикла. Если шаг цикла равен 1, то hx можно опустить, и в этом случае оператор for будет таким.
for x=xn:xk
операторы
end
Выполнение цикла начинается с присвоения параметру стартового значения (x = xn).
Затем следует проверка, не превосходит ли параметр конечное значение (x xk).
Если x xk, то цикл считается завершенным, и управление передается следующему за телом цикла оператору. Если же x 6 xk, то выполняются операторы в цикле (тело цикла).
Далее параметр цикла увеличивает свое значение на hx (x = x + hx).
После чего снова производится проверка значения параметра цикла, и алгоритм повторяется.
Заключение
Система Scilab предназначена для численных расчетов и работы с матрицами. Кроме того, она обладает развитыми средствами программирования (включая отладчик скриптов), так что ее можно рассматривать и как систему разработки высокотехнологичных приложений. В Scilab встроен мощный язык программирования с поддержкой объектов. Работа в Scilab может осуществляться в режиме командной строки и в программном режиме. Особенностью пакета является то, что он предназначен исключительно для реализации численных методов и по умолчанию оперирует с любыми значениями как с числами с плавающей точкой. В этой программе очень хорошо реализована линейная алгебра, матричное исчисление, работа со статистическими функциями, а также графика и симуляция различных процессов.
Промышленный цикл и его фазы
... в целом. Цель работы: Изучить промышленный цикл и его фазы. Задачи исследования: 1. Рассмотреть типологию экономических циклов; классификацию и периодичность кризисов. 2. Выявить причины экономических кризисов и циклов. 3. Проанализировать промышленный цикл и его фазы. 4. Рассмотреть современные особенности ...
Список использованной литературы
[Электронный ресурс]//URL: https://inzhpro.ru/referat/po-sistemam-avtomaticheskogo-upravleniya-scilab/
1. Дьяконов, В. П. Справочник по применению системы PC MATLAB. — М.: «Физматлит», 1993. — С. 112.
2. Дьяконов, В. П. Компьютерная математика. Теория и практика. — СПб: «Питер», 1999, 2001. — С. 1296.
3. Дьяконов, В. П. MATLAB 5 — система символьной математики. — М.: «Нолидж», 1999. — С. 640.
4. Дьяконов, В.П., Абраменкова И.В. MATLAB. Обработка сигналов и изображений. Специальный справочник. — СПб.: «Питер», 2002. — С. 608.
5. Алексеев, Е. Р. Scilab. Решение инженерных и математических задач. — Москва ALT Linux; БИНОМ. Лаборатория знаний 2008.
