— устройства, предназначенные для обработки информации в цифровой форме (последовательности сигналов высокого — «1» и низкого — «0» уровней в двоичной логике, последовательность «0», «1» и «2» в троичной логике, последовательности «0», «1», «2», «3», «4», «5», «6», «7», «8»и «9» в десятичной логике).
Физически логические элементы могут быть выполнены механическими, электромеханическими (на электромагнитных реле), электронными (на диодах и транзисторах), пневматическими, гидравлическими, оптическими и др.
С развитием электротехники от механических логических элементов перешли к электромеханическим логическим элементам (на электромагнитных реле), а затем к электронным логическим элементам на электронных лампах, позже — на транзисторах. После доказательства в 1946 г. теоремы Джона фон Неймана о экономичности показательных позиционных систем счисления стало известно о преимуществах двоичной и троичной систем счисления по сравнению с десятичной системой счисления. От десятичных логических элементов перешли к двоичным логическим элементам. Двоичность и троичность позволяет значительно сократить количество операций и элементов, выполняющих эту обработку, по сравнению с десятичными логическими элементами.
Логические элементы выполняют логическую функцию (операцию) с входными сигналами (операндами, данными).
Всего возможно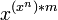 
логических функций и соответствующих им логических элементов, где — основание системы счисления, — число входов (аргументов), — число выходов, т.е. бесконечное число логических элементов. Поэтому в данной статье рассматриваются только простейшие и важнейшие логические элементы.
Всего возможны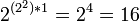 
двоичных двухвходовых логических элементов и 
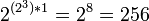двоичных трёхвходовых логических элементов (Булева функция).
Кроме 16 двоичных двухвходовых логических элементов и 256 трёхвходовых двоичных логических элементов возможны 19 683 двухвходовых троичных логических элемента и 7 625 597 484 987 трёхвходовых троичных логических элементов (троичные функции).
1. Двоичные логические операции с цифровыми сигналами (битовые операции)
Логические основы цифровой техники
... последовательностным устройством. 2. Способы задания логических функций логический цифровой шифратор В классической математике для ... 0 X 1 и X2 несовместны Логическое И-НЕ; элемент (штрих) Шеффера; отрицание конъюнкции X ... Логическое НЕ; инверсия; логическое отрицание 1 0 элементарными логическими функциями, Рассмотрим способ построения таблиц истинности для сложных функций многих переменных. двоичной ...
Логические операции (булева функция) своё теоретическое обоснование получили в алгебре логики.
Логические операции с одним операндом называются унарными , с двумя — бинарными , с тремя — тернарными (триарными , тринарными ) и т. д.
Из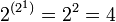 
возможных унарных операций с унарным выходом интерес для реализации представляют операции отрицания и повторения, причём, операция отрицания имеет большую значимость, чем операция повторения, так как повторитель может быть собран из двух инверторов, а инвертор из повторителей не собрать.
1.1. Отрицание, НЕТ, НЕ
| A | B = A |
|---|---|
| 0 | 1 |
| 1 | 0 |
Мнемоническое правило для отрицания звучит так: На выходе будет:
- «1» тогда и только тогда, когда на входе «0»,
- «0» тогда и только тогда, когда на входе «1»
1.2. Повторение, ДА
| A | B = A |
|---|---|
| 0 | 0 |
| 1 | 1 |
Преобразование информации требует выполнения операций с группами знаков, простейшей из которых является группа из двух знаков. Оперирование с большими группами всегда можно разбить на последовательные операции с двумя знаками.
Из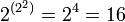 
возможных бинарных логических операций с двумя знаками c унарным выходом интерес для реализации представляют 10 операций, приведённых ниже.
1.3. Конъюнкция (логическое умножение).
Операция 2И. Функция min(A,B)
| A | B | f (AB ) |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
Логический элемент, реализующий функцию конъюнкции, называется схемой совпадения. Мнемоническое правило для конъюнкции с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда на всех входах действуют «1»,
- «0» тогда и только тогда, когда хотя бы на одном входе действует «0»
1.4. Дизъюнкция (логическое сложение).
Операция 2ИЛИ. Функция max(A,B)
| A | B | f (AB ) |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 1 |
Мнемоническое правило для дизъюнкции с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда хотя бы на одном входе действует «1»,
- «0» тогда и только тогда, когда на всех входах действуют «0»
1.5. Инверсия функции конъюнкции. Операция 2И-НЕ (штрих Шеффера)
| A | B | f (AB ) |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Мнемоническое правило для И-НЕ с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда хотя бы на одном входе действует «0»,
- «0» тогда и только тогда, когда на всех входах действуют «1»
1.6. Инверсия функции дизъюнкции. Операция 2ИЛИ-НЕ (стрелка Пирса)
| A | B | f (AB ) |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Мнемоническое правило для ИЛИ-НЕ с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда на всех входах действуют «0»,
- «0» тогда и только тогда, когда хотя бы на одном входе действует «1»
1.7. Эквивалентность (равнозначность), 2ИСКЛЮЧАЮЩЕЕ_ИЛИ-НЕ
XNOR gate
| A | B | f (AB ) |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Мнемоническое правило эквивалентности с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда на входе действует четное количество «1»,
- «0» тогда и только тогда, когда на входе действует нечетное количество «1»
1.8. Сложение по модулю 2 (2Исключающее_ИЛИ, неравнозначность).
Инверсия равнозначности.
В англоязычной литературе 2XOR.
[Электронный ресурс]//URL: https://inzhpro.ru/referat/osnovyi-tsifrovoy-tehniki/
| A | B | f (AB ) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Мнемоническое правило для суммы по модулю 2 с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда на входа действует нечётное количество «1»,
- «0» тогда и только тогда, когда на входа действует чётное количество «1»
1.9. Импликация от A к B (инверсия декремента)
| A | B | f (AB ) |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Мнемоническое правило для инверсии декремента звучит так: На выходе будет:
- «0» тогда и только тогда, когда на «B» меньше «А»,
- «1» тогда и только тогда, когда на «B» больше либо равно «А»
1.10. Импликация от B к A (инверсия инкремента)
| A | B | f (AB ) |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Мнемоническое правило для инверсии инкремента звучит так: На выходе будет:
- «0» тогда и только тогда, когда на «B» больше «А»,
- «1» тогда и только тогда, когда на «B» меньше либо равно «А»
1.11. Декремент. Запрет импликации по B. Инверсия импликации от A к B
| A | B | f (AB ) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Мнемоническое правило для инверсии импликации от A к B звучит так: На выходе будет:
- «1» тогда и только тогда, когда на «A» больше «B»,
- «0» тогда и только тогда, когда на «A» меньше либо равно «B»
1.12. Инкремент. Запрет импликации по A. Инверсия импликации от B к A
| A | B | f (AB ) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Мнемоническое правило для инверсии импликации от B к A звучит так: На выходе будет:
- «1» тогда и только тогда, когда на «B» больше «A»,
- «0» тогда и только тогда, когда на «B» меньше либо равно «A»
Примечание 1, Примечание 2
функционально полным логическим базисом
- И, НЕ (2 элемента)
- ИЛИ, НЕ (2 элемента)
- И-НЕ (1 элемент)
- ИЛИ-НЕ (1 элемент).
Для преобразования логических функций в один из названых базисов необходимо применять Закон (правило) де-Моргана.
2. Физические реализации логических элементов
Физические реализации одной и той же логической функции в разных системах электронных и неэлектронных элементов отличаются друг от друга.
3. Классификация электронных транзисторных физических реализаций логических элементов
Логические элементы подразделяются и по типу использованных в них электронных элементов. Наибольшее применение в настоящее время находят следующие логические элементы:
- РТЛ (резисторно-транзисторная логика)
- ДТЛ (диодно-транзисторная логика)
- ТТЛ (транзисторно-транзисторная логика)
Обычно входной каскад логических элементов ТТЛ представляет собой простейшие компараторы, которые могут быть выполнены различными способами (на многоэмиттерном транзисторе или на диодной сборке).
В логических элементах ТТЛ входной каскад, кроме функций компараторов, выполняет и логические функции. Далее следует выходной усилитель с двухтактным (двухключевым) выходом.
В логических элементах КМОП входные каскады также представляют собой простейшие компараторы. Усилителями являются КМОП-транзисторы. Логические функции выполняются комбинациями параллельно и последовательно включенных ключей, которые одновременно являются и выходными ключами.
Транзисторы могут работать в инверсном режиме, но с меньшим коэффициентом усиления. Это свойство используются в ТТЛ многоэмиттерных транзисторах. При подаче на оба входа сигнала высокого уровня (1,1) первый транзистор оказывается включенным в инверсном режиме по схеме эмиттерного повторителя с высоким уровнем на базе, транзистор открывается и подключает базу второго транзистора к высокому уровню, ток идёт через первый транзистор в базу второго транзистора и открывает его. Второй транзистор «открыт», его сопротивление мало и на его коллекторе напряжение соответствует низкому уровню (0).
Если хотя бы на одном из входов сигнал низкого уровня (0), то транзистор оказывается включенным по схеме с общим эмиттером, через базу первого транзистора на этот вход идёт ток, что открывает его и он закорачивает базу второго транзистора на землю, напряжение на базе второго транзистора мало и он «закрыт», выходное напряжение соответствует высокому уровню. Таким образом, таблица истинности соответствует функции 2И-НЕ.
- ТТЛШ (то же с диодами Шоттки)
Для увеличения быстродействия логических элементов в них используются транзисторы Шоттки (транзисторы с диодами Шоттки), отличительной особенностью которых является применение в их конструкции выпрямляющего контакта металл-полупроводник вместо p-n перехода. При работе этих приборов отсутствует инжекция неосновных носителей и явления накопления и рассасывания заряда, что обеспечивает высокое быстродействие. Включение этих диодов параллельно коллекторному переходу блокирует насыщение выходных транзисторов, что увеличивает напряжения логических 0 и 1, но уменьшает потери времени на переключение логического элемента при том же потребляемом токе (или позволяет уменьшить потребляемый ток при сохранении стандартного быстродействия).
Так, серия 74хх и серия 74LSxx имеют приблизительно равное быстродействие (в действительности, серия 74LSxx несколько быстрее), но потребляемый от источника питания ток меньше в 4-5 раз (во столько же раз меньше и входной ток логического элемента).
- КМОП (логика на основе комплементарных ключей на МОП транзисторах)
- ЭСЛ (эмиттерно-связанная логика)
Эта логика, иначе называемая логикой на переключателях тока, построена на базе биполярных транзисторов, объединённых в дифференциальные каскады. Один из входов обычно подключён внутри микросхемы к источнику опорного (образцового) напряжения, примерно посредине между логическими уровнями. Сумма токов через транзисторы дифференциального каскада постоянна, в зависимости от логического уровня на входе изменяется лишь то, через какой из транзисторов течёт этот ток. В отличие от ТТЛ, транзисторы в ЭСЛ работают в активном режиме и не входят в насыщение или инверсный режим. Это приводит к тому, что быстродействие ЭСЛ-элемента при той же технологии (тех же характеристиках транзисторов) гораздо больше, чем ТТЛ-элемента, но больше и потребляемый ток. К тому же, разница между логическими уровнями у ЭСЛ-элемента намного меньше, чем у ТТЛ (меньше вольта), и, для приемлемой помехоустойчивости, приходится использовать отрицательное напряжение питания (а иногда и применять для выходных каскадов второе питание).
Зато максимальные частоты переключения триггеров на ЭСЛ более, чем на порядок превышают возможности современных им ТТЛ, например, серия К500 обеспечивала частоты переключения 160-200 МГц, по сравнению с 10-15 МГц современной ей ТТЛ серии К155. В настоящее время и ТТЛ(Ш), и ЭСЛ практически не используются, так как с уменьшением проектных норм КМОП технология достигла частот переключения в несколько гигагерц.
3.1. Инвертор
Одним из основных логических элементов является инвертор. Инвертирующими каскадами являются однотранзисторный каскад с общим эмиттером, однотранзисторный каскад с общим истоком, двухтранзисторный двухтактный выходной каскад на комплементарных парах транзисторов с последовательным включением транзисторов по постоянному току (применяется в ТТЛ и КМОП), двухтранзисторный дифференциальный каскад с параллельным включением транзисторов по постоянному току (применяется в ЭСЛ) и др. Но одного условия инвертирования недостаточно для применения инвертирующего каскада в качестве логического инвертора. Логический инвертор должен иметь смещённую рабочую точку на один из краёв проходной характеристики, что делает каскад неустойчивым в середине диапазона входных величин и устойчивым в крайних положениях (закрыт, открыт).
Такой характеристикой обладает компаратор, поэтому логические инверторы строят как компараторы, а не как гармонические усилительные каскады с устойчивой рабочей точкой в середине диапазона входных величин. Таких каскадов, как и контактных групп реле, может быть два вида: нормально закрытые (разомкнутые) и нормально открытые (замкнутые).
4. Применение логических элементов
Логические элементы входят в состав микросхем, например ТТЛ элементы — в состав микросхем К155 (SN74), К133; ТТЛШ — 530, 533, К555, ЭСЛ — 100, К500 и т. д.
5. Комбинационные логические устройства
Комбинационными
- Шифратор
- Дешифратор
- Мультиплексор
- Демультиплексор
- Полусумматор
- Сумматор
Все они выполняют простейшие двоичные, троичные или n-ичные логические функции.
6. Последовательностные цифровые устройства
Последовательностными
- Триггер
- Счётчик импульсов
- Регистр
- Венъюнктор
- Секвентор
Данный реферат составлен на основе .
