ПРИЛОЖЕНИЯ………………………………………………………………………………………………………………………………….
В настоящее время логистика выступает как научное направление, которое играет ведущую роль в рационализации и автоматизации производства. Эта наука охватывает вопросы снабжения предприятия сырьем, материалами, полуфабрикатами, организацию сбыта и распределения, то есть осуществляет транспортировку готовой продукции.
Логистика базируется на кибернетике, исследовании операций, теории систем, экономической теории, экономике отрасли и др.
Основной целью логистики является рациональное управление материальными потоками для удовлетворения спроса и доставки грузов точно в срок. Парадигма логистики: нужный товар нужного качества в нужном месте и в нужный срок. Концепция логистики — построение интегрированных логистических систем начиная от этапа проектирования до утилизации вторсырья и отходов.
Суть данной курсовой работы заключается в выработке оптимального решения для доставки нерудных строительных материалов на объекты строительства с минимальными затратами на доставку и с минимальными потерями времени. По ходу выполнения курсовой работы встает вопрос о решении комплекса взаимосвязанных задач, результаты каждой из которых является исходными данными для следующих.
Необходимо решить следующие задачи:
1. Найти кратчайшие пути в транспортной сети.
2. Закрепить пункты назначения за пунктами отправления.
3. Определить оптимальный состава транспортных средств, использующихся для перевозки строительных материалов.
4. Определить поток ресурсов минимальной стоимости.
Все эти задачи являются актуальными для любого типа производства, особенно в условиях новой, рыночной экономики, когда (по данным статистики в настоящее время около 2% времени затрачивается на производство продукции и 85% на ее транспортировку к месту назначения. ) время и стоимость доставки продукции потребителям непосредственно влияет на экономические показатели эффективности работы предприятия.
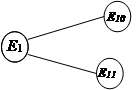
Имеются три карьера с песком (пункты Е 1 , Е2 и Е3 ).
Из этих карьеров песок через ряд промежуточных пунктов Е4 -Е9 направляется на строящиеся дороги (пункты Е10 , Е11 ).
Управление качеством продукции на предприятии
... задачей является обеспечение выпуска продукции, соответствующей требованиям рынка, приемлемой в отношении цены и качества, то есть конкурентоспособной. 1. Теоретические основы изучения качества продукции на предприятии 1.1 Понятие качества и его роль в ...
Транспортная сеть(схема 1), по которой производится перевозка, представляет собой неориентированный граф G=(Е, е), где Е — вершины графа, соответствующие конечным и промежуточным пунктам перевозки, а е — ребра, соединяющие вершины графа, в данном случае — дороги, по которым перевозятся нерудные строительные материалы.
Пункты отправления (т.е. карьеры) обслуживаются экскаваторами с базы механизации, каждый из которых имеет определенную производительность.
Песок с карьеров на строящиеся дороги перевозится с помощью автосамосвалов, которые имеются на автотранспортном предприятии.
Над ребрами указаны расстояния между соседними узлами (км); объемы песка в пунктах отправления и потребность в нем в пунктах назначения приведена в таблице 1.
Задача состоит в том, чтобы закрепить пункты отправления за пунктами назначения, определить оптимальный количественный и качественный состав автосамосвалов, которые перевозят требуемый объем песка с карьеров на объекты строительства, и составить почасовой график работы этих автосамосвалов.
Таблица 1.
| i (номер пункта) | Объем песка, имеющегося в i-м пункте отправления, тыс. м3 (а i). |
Объем песка, требующегося в i-м пункте назначения, тыс. м3 ( bj). |
| 1 | 48 | 65 |
| 2 | 22 | 40 |
| 3 | 35 |
![]() (1)
(1)
В таблице 2 представлены типы и некоторые характеристики экскаваторов, работающих на карьерах 1-3.
Характеристики экскаваторов
| Номер карьера | Марка экскаватора | Объем ковша, м3 |
| 1 | Э-6525 | 0,65 |
| 2 | Э — 10011Е | 1,00 |
| 3 | Э — 1252Б | 1,25 |
Для перевозки песка используются имеющиеся на АТП автосамосвалы с грузоподъемностью 7, 10, 27тонн.
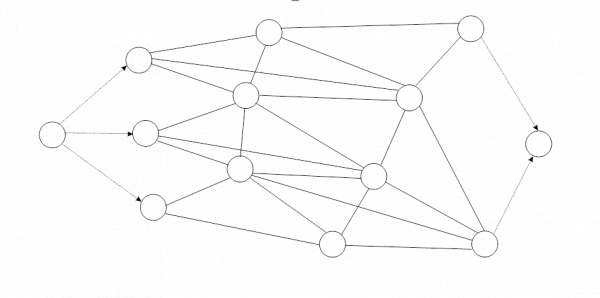
Схема 1. “Транспортная сеть с ограниченными пропускными способностями”.
Задача заключается в определении стоимости перевозки 1 м 3 песка на расстояние, соответствующее длине каждого ребра.
Стоимость транспортировки 1 м 3 песка на 1997 год в долларах США определяется по формуле:
- Сij = (С(l) * 1,02 * 1,57 * 7500*r) / 6000; (2)
где С(l) — тарифная плата за перевозку 1 тпеска на 1 км., руб. Она является переменной величиной и зависит от расстояния Lij (таблица 2);
- r — плотность песка (1.6 т/м 3 ).
Прочие сомножители являются поправочными коэффициентами, которые учитывают изменение величины тарифной платы вследствие инфляции и влияния рыночных факторов.
Таблица 3 Тарифная плата за перевозку 1 т. груза
| Расстояние, км | Тарифная плата за перевозку 1 т. груза 1-го км , руб на 1984 год | Расстояние, км | Тарифная плата за перевозку 1 т. груза 1-го км , руб на 1984 год |
| 1 | 0,25 | 16 | 1 |
| 2 | 0,30 | 17 | 1,04 |
| 3 | 0,35 | 18 | 1,08 |
| 4 | 0,40 | 19 | 1,12 |
| 5 | 0,45 | 20 | 1,16 |
| 6 | 0,50 | 21-25 | 1,28 |
| 7 | 0,55 | 26-30 | 1,48 |
| 8 | 0,60 | 31-35 | 1,68 |
| 9 | 0,65 | 36-40 | 1,88 |
| 10 | 0,70 | 41-45 | 2,06 |
| 11 | 0,75 | 46-50 | 2,21 |
| 12 | 0,80 | 51-60 | 2,44 |
| 13 | 0,85 | 61-70 | 2,72 |
| 14 | 0,90 | 71-80 | 2,92 |
| 15 | 0,95 | 81-90 | 3,12 |
|
Свыше — за 1 км+ 3,4 коп |
91-100 | 3,32 | |
Рассчитываем стоимость перевозок исходя из расстояний, указанных на ребрах транспортной сети:
Таблица 4. Локальные стоимости перевозок.
| Ребро (ЕiЕj) | Расстояние,км | Стоимость перевозки, долл/м 3 |
| Е1-Е9 | 15 | 3,04 |
| Е9-Е10 | 15 | 3,04 |
| Е9-Е11 | 10 | 2,24 |
| Е2-Е5 | 11 | 2,40 |
| Е5-Е6 | 6 | 1,60 |
| Е6-Е10 | 20 | 3,71 |
| Е6-Е9 | 13 | 2,72 |
| Е9-Е11 | 10 | 2,24 |
| Е3-Е4 | 14 | 2,88 |
| Е4-Е8 | 12 | 2,56 |
| Е8-Е9 | 19 | 3,59 |
| Е9-Е10 | 15 | 3,04 |
| Е4-Е11 | 11 | 2,40 |
Задача заключается в нахождении ребер, соединяющих каждый пункт отправления с каждым пунктом назначения и имеющих минимальную суммарную длину.
Задача решается составлением минимального дерева-остова.
Алгоритм, в конечном счете, сводится к перебору последовательно всех возможных вариантов пути и выбору из них кратчайшего.
Расчет кратчайшего пути производится по формуле:
Uj=(Ui+Lij),
где Uj — кратчайшее расстояние до текущего пункта j,км;
- Ui — кратчайшее расстояние до предыдущего пункта i,км;
- Lij — расстояние между i и j пунктами,км.
В результате решения этой задачи мы получили набор из 6 кратчайших маршрутов, соединяющих между собой все пункты отправления и все пункты назначения.
Ниже, в таблице 5, представлены эти маршруты с указанием промежуточных пунктов, через которые они проходят, и общей длины маршрута.
Таблица 5.
| Маршрут | Промежуточные пункты | Стоимость перевозки 1м3 песка по маршруту, тыс. руб. | Длина мар-шрута, км |
| Е1 Е10 | Е1 -Е 9 -Е 10 | 4,74 | 30 |
| Е1 Е11 | Е1 -Е9 -Е11 | 4,09 | 25 |
| Е2 Е10 | Е2 -Е5 -Е6 -Е10 | 6,02 | 37 |
| Е2 Е11 | Е2 -Е5 -Е6 -Е9 -Е11 | 6,02 | 40 |
| Е3 Е10 | Е3 -Е4 -Е8 -Е9 -Е10 | 7,81 | 60 |
| Е3 Е11 | Е3 -Е4 -Е11 | 4,09 | 25 |
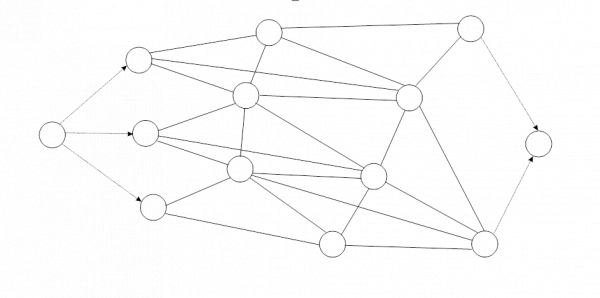
Схема 2.Графическое изображение найденных кратчайших путей в сети
Целью транспортной задачи является нахождение наиболее рационального способа распределения ресурсов, находящихся в пунктах отправления, по пунктам назначения, с учетом стоимости доставки ресурсов.
Исходные данные для решения транспортной задачи представляют собой матрицу. В клетках этой матрицы сверху указаны стоимости (Cij) перевозки 1 м 3 груза из i-го пункта отправления в j-й пункт назначения, а в нижней части клеток будут показаны объёмы перевозок по этому маршруту (Xij).
Целевая функция транспортной задачи заключается в минимизации общей стоимости всех перевозок:
F =![]() ® min
® min
Ход решения задачи:
1. Приводим исходную матрицу (вычитаем из Сij каждой строки минимальное значение Сij в этой строке; затем для столбцов, в которых нет ни одного нуля, из каждого Сij в столбце вычитаем минимальное Сij).
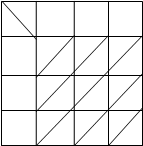 |
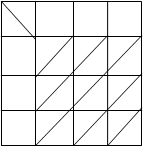 |
|
|||
|
|||
|
|
2. Проводим первичное распределение потока ресурсов по клеткам с нулевой стоимостью и закрываем столбцы и строки.
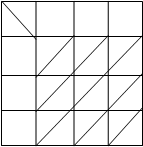 |
3. Поскольку распределение оказалось неоптимальным, т.е. не все столбцы оказались закрытыми, проводим преобразование: выбираем минимальное Cij среди клеток, стоящих на пересечении открытых столбцов и открытых строк, и вычитаем это значение Cij из значений Cij открытых столбцов и прибавляем его к Cij закрытых строк. Перераспределяем поток
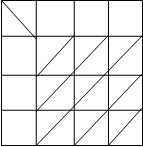
4. Распределение все еще не оптимально, но появилась цепочка, т.е. последовательность клеток с Cij, равным последовательно 0®0*®0’. Переносим 35 единиц потока вдоль цепочки. Перераспределяем поток , и получаем оптимальную матрицу.
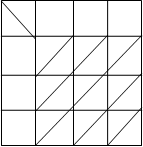 |
Стоимость перевозок, соответствующая оптимальному плану, равна
C= 43000*6,08 + 5000*5,28 + 22000*7,71 + 35000*5,28 = 642260 долл..
Оптимальные объемы перевозок, полученные в результате решения транспортной задачи:
Е 1 Е10 = 43000 м3
Е 1 Е11 = 5000 м3
Е 2 Е10 = 22000 м3
Е 3 Е11 = 35000 м3
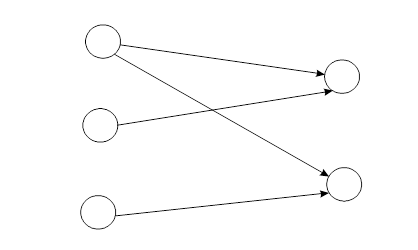
Схема 3. Маршруты перевозок песка от каждого карьера до каждого пункта назначения.
Рассмотрим маршрут Е 2 Е10. Он представляет собой одноканальную замкнутую систему массового обслуживания с вызовом из одного источника.
Расстояние между пунктами 37 км.
Необходимые формулы для расчетов:
T ц = tож + tпогр + 2L*60/vср + tм + tразг (1)
T ц — продолжительность цикла автосамосвала, мин.
T ож — время ожидания, мин.
T погр — время погрузки, мин.
L — расстояние между пунктами, км.
v ср — средняя скорость автосамосвала, км/ч (50 км/ч).
T м — время маневрирования, мин.
T разг — время разгрузки, мин.
Количество автосамосвалов определяется по формуле
m1 = t ц / tпогр (2)
Эта формула применима в том случае, если автосамосвалы подаются под загрузку равномерно, а продолжительность погрузки имеет незначительные отклоненияот среднего значения tц.
В реальной ситуации величины являются случайными и зависят от множества факторов, определяемых работой в забое и транспортными условиями. В результате этого в некоторые моменты времени возникнут простои экскаватора или автосамосвалов, что приведет к нарушению согласованной работы.
Поэтому для расчета машин применяется дополнительная формула:
m2 = Пэ/Па (3)
Коэффициент ожидания (загрузки) определяется по формуле
![]() (4)
(4)
Таблица 6. Продолжительность погрузки автосамосвалов.
| Емкость ковша,м 3 | Грузоподъемность автосамосвала,т | Время погрузки,мин |
| 0,65 | 4,5 | 1 |
| 6,0 | 1,7 | |
| 1,00 | 7,0 | 2,0 |
| 10,0 | 3,8 | |
| 1,25 | 27,0 | 9,2 |
Оптимальный комплект машин выбирается из различных комбинаций марок экскаваторов и автосамосвалов.
Таблица 7. Варианты комбинаций марок экскаваторов и автосамосвалов.
| Номер варианта | 1 | 2 | 3 | 4 | 5 |
| Емкость ковша экскаватора, м 3 | 0,65 | 1,00 | 1,25 | ||
| Грузоподъемность автосамосвала,т | 4,5 | 6 | 7 | 10 | 27 |
Производительность экскаватора с объемом ковша 1 м 3 и нормой выработки 100 м3 за 1.2 часа составляет
Пэ = 100/1,2 = 83,33 м 3 /час.
Производительность экскаватора с объемом ковша 0,65 м 3 с нормой выработки 100 м3 за 1,45 часа равна
Пэ = 100/1,45=68,97 м 3 /час.
Производительность экскаватора с объемом ковша 1,25 м 3 с нормой выработки 100 м3 за 0,89 часа равна
Пэ = 100/0,89=112,35 м 3 /час.
Производительность одного автосамосвала определяется по формуле
Па = Qa* Кисп * Кв / (tц*x), где (5)
Па — производительность автосамосвала, м 3 /час;
- Qa — грузоподъемность автосамосвала, т;
- Кисп — коэффициент использования грузоподъемности;
Кв — коэффициент использования по времени (0,9)
tц — продолжительность цикла автосамосвала, час;
x — плотность материала, т/ м 3 .
1. Па = 1,48 м 3 /ч
2. Па = 1,96 м 3 /ч
3. Па = 2,27 м 3 /ч
4. Па = 3,18 м 3 /ч
5. Па = 8,12 м 3 /ч
Количество машин определяется по формулам (1) и (2).
В таблице 6 рассматривается семейство автосамосвалов q* = {4,5; 6; 7; 10; 27}.
T ц 4.5 = 1,5+1+2*37*60/50+0,5+0,5=92,3 мин
T ц 6 =1,5+1,7+2*37*60/50+0,5+0,5= 93 мин.;
T ц 7 =1,5+2+2*37*60/50+0,5+0,5= 93,3мин.;
T ц 10 =1,5+3,8+2*37*60/50+0,5+1= 95,6 мин.;
T ц 27 =1,5+9,2+2*37*60/50+0,5+1= 101 мин.;
Таблица 8
| Грузоподъемность автосамосвала, т | Объем ковша, м3 |
Tцикла , мин. |
Требуемое количество машин ( m) |
Коэффициент ожидания ( a) | |
| 4,5 | 0,65 | 92,3 | 92 | 47 | 0,01 |
| 6 | 93 | 55 | 36 | 0,018 | |
| 7 | 1,00 | 93,3 | 47 | 37 | 0,021 |
| 10 | 95,6 | 25 | 27 | 0,039 | |
| 27 | 1,25 | 101 | 11 | 14 | 0,091 |
Оптимальная структура транспортных средств из всех вариантов подбирается на основе минимальных приведенных затрат и максимальной производительности.
Поскольку АТП может предоставить не более 30 машин, то рассмотрению подлежат только автосамосвалы с грузоподъемностью 10 и 27 тонн.
Относительная эффективность использования машин проверялась с помощью программы “mod1” на ПЭВМ “Искра 1080”. Результаты работы программы представлены в таблице 5.
Таблица 9
| Грузоподъемность автосамосвала, т | p (коэффициент простоя экскаватора) | w (средняя длина очереди) |
| 10 | 0,1789 (для т=25) | 2,7661 |
| 27 | 0,2815 | 2,0220 |
( т.к. коэффициент простоя экскаватора должен находиться в интервале 0,15-0,18)
Определение суммарной производительности автосамосвалов
Суммарная производительность автосамосвалов на этом маршруте составляет
SПа= 3,18*25= 79,50 м 3 /час
Производительность экскаватора с объемом ковша 1 м 3 и нормой выработки 100 м3 за 1.2 часа составляет
Пэ = 100/1,2 = 83,33 м 3 /час.
Однако, если учесть, что 17,89% своего времени экскаватор простаивает, что его производительность равна Пэ’=83,33*(1-0,1789) = 68,42 м 3 /час, так что соблюдается неравенство
Пэ <m*Па
Расчет приведенных затрат
производится по формуле
Пз=Сэ(1-р 0 ) + ЕнQэ + m[a+b*1n(1-j)+ ЕнQa], где
Пз — приведенные затраты;
- Сэ — стоимость машино-часа экскаватора, руб. (37,04/8)
р 0 — коэффициент простоя экскаватора (0,1789)
Ен — нормативный коэффициент эффективности,равный 0,12
Qэ, Qa — инвентарно-расчетная стоимость экскаватора и автосамосвала в расчете на машино-час,(Qэ’ = 21175/3075, Qa = 9170/2750 ),
m — количество автосамосвалов (25)
a — часть стоимость машино — часа, не зависящая от прбега. автосамосвала, руб. (11,07/8)
b — затраты, приходящиеся на 1 км пробега самосвала, руб. (0,261)
j — коэффициент простоя (j=w/m=2,7661 /25),
где w — среднее число автосамосвалов в очереди(w = т-(1-р 0 )/а;
Вероятность простоя экскаватора определяется по формуле:
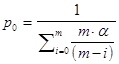 ;
;
— Таблица 10. Технико-экономические составляющие затрат на самосвал.
| Грузоподъемность автосамосвала, т | а | b | Qa |
| 4,5 | 0,850 | 0,127 | 1,313 |
| 6 | 1,039 | 0,156 | 1,923 |
| 7 | 1,165 | 0,176 | 2,335 |
| 10 | 1,384 | 0,261 | 3,335 |
| 27 | 2,510 | 0,551 | 9,507 |
Таблица 11 Технико-экономические составляющие затрат на экскаватор
| Обем ковша, м 3 | Сэ | Qэ | Продолжительность рабочего цикла |
| 0,65 | 3,911 | 4,608 | 16,6 |
| 1,00 | 4,63 | 6,886 | 17,2 |
| 1,25 | 4,890 | 8,020 | 18 |
Пз = 37,04/8*(1-0,1789)+0,12*21175/3075+25*(11,07/8+0,261*50 (1-0,110)+0,12*9170/2750) = 340,4 руб.
Удельные затраты:
Пу = Пз / Пэ(1-р 0 ) кэ, где
Пэ — производительность экскаватора, м 3 /час
Кэ — коэффициент перевыполнения производительности ведущей машины, равный 1,15;
Пу = 340,4/(83,33*(1-0,1789)) 1,15=4,3358 р/(м 3 /час).
Рассмотрим маршрут Е 3 Е11. Он представляет собой одноканальную замкнутую систему массового обслуживания с вызовом из одного источника.
Расстояние между пунктами 25 км.
Необходимые формулы для расчетов (1), (2), (3).
Производительность экскаватора с объемом ковша 1 м 3 и нормой выработки 100 м3 за 1.2 часа составляет
Пэ = 100/1,2 = 83,33 м 3 /час.
Производительность экскаватора с объемом ковша 0,65 м 3 с нормой выработки 100 м3 за 1,45 часа равна
Пэ = 100/1,45=68,97 м 3 /час.
Производительность экскаватора с объемом ковша 1,25 м 3 с нормой выработки 100 м3 за 0,89 часа равна
Пэ = 100/0,89=112,35 м 3 /час.
2. Па = 2,80 м 3 /ч
3. Па = 3,26 м 3 /ч
4. Па = 4,48 м 3 /ч
5. Па = 10,72 м 3 /ч
В таблице 6 рассматривается семейство автосамосвалов q* = {4,5; 6; 7; 10; 27}.
T ц 4.5 = 1,5+1+2*37*60/50+0,5+0,5 = 65,2мин.;
T ц 6 =1,5+1,7+2*37*60/50+0,5+0,5= 65,5 мин.;
T ц 7 =1,5+2+2*37*60/50+0,5+0,5= 67,8мин.;
T ц 10 =1,5+3,8+2*37*60/50+0,5+1= 76,5 мин.;
T ц 27 =1,5+9,2+2*37*60/50+0,5+1= 101 мин.;
Таблица 12.
| Грузоподъемность автосамосвала, т |
Tцикла , мин. |
Требуемое количество машин ( m) |
Коэффициент ожидания ( a) | |
| 6 | 65,2 | 24 | 25 | 0,023 |
| 7 | 67,5 | 22 | 26 | 0,030 |
| 10 | 67,8 | 14 | 19 | 0,038 |
| 27 | 76,5 | 6 | 11 | 0,081 |
Относительная эффективность использования машин проверялась с помощью программы “mod1” на ПЭВМ “Искра 1080”. Результаты работы программы представлены в таблице 5.
Таблица 13
| Грузоподъемность автосамосвала, т | p (коэффициент простоя экскаватора) | w (средняя длина очереди) |
| 6 | 0,1718(т=24) | 2,668 |
| 7 | 0,1575(т=26) | 2,4342 |
| 10 | 0,0770(т=19) | 2,0810 |
| 27 | 0,1567(т=14) | 2,0220 |
Как видно из таблицы 5, оптимальные показатели простоя наблюдаются у автосамосвалов с грузоподъемностью 6,7,27 тонн.
Таблица 14. Определение оптимального сотава комплекта машин.
| Объем ковша, м 3 | Грузоподъемность автосамосвала, т | Количество автосамосвалов | Приведенные затраты, руб | Удельные приведенные затраты, руб |
| 0,65 | 6 | 24 | 200,59 | 1,04 |
| 1,00 | 7 | 26 | 253,59 | 1,032 |
| 1,25 | 27 | 14 | 386,31 | 1,031 |
Оптимальная структура транспортных средств из всех вариантов подбирается на основе минимальных приведенных затрат и максимальной производительности.
На основании полученных данных можно определить, что оптимальным вариантом будет пустить по лучу 14 двадцатисемитонных автосамосвалов.
Определение суммарной производительности автосамосвалов
Производительность каждого из автосамосвалов, использующихся на маршруте Е 3 Е11 , равна
Па = 10,72 м 3 /час;
Суммарная производительность автосамосвалов на этом маршруте составляет
SПа= 10,72*14 = 150,08 м 3 /час
Производительность экскаватора с объемом ковша 1,25 м 3 с нормой выработки 100 м3 за 0,89 часа равна
Пэ = 100/0,89=112,35 м 3 /час.
Однако, если учесть, что 15,67% своего времени экскаватор простаивает, что его производительность равна Пэ’=112,35*(1-0,1567) = 94,74 м 3 /час, так что соблюдается неравенство
Пэ <m*Па
|
Из карьера Е 1 обслуживаются два объекта строительства: Е10 и Е11.
Таким образом, эта система является одноканальной замкнутой системой массового обслуживания с вызовом из двух источников.
Расчет количества машин производится по формулам (1) и (2).
В таблице 6 приведены результаты расчетов по семейству автосамосвалов q* = {6; 7; 10; 27} для маршрута Е1 Е10 длиной 30 км .
T ц 6 =1,5+2,7+2*36*60/50+0,5+0,5= 77,2 мин.;
T ц 7 =1,5+3+2*36*60/50+0,5+0,5=77,5 мин.;
T ц 10 =1,5+4,8+2*36*60/50+0,5+1=79,8 мин.;
T ц 27 =1,5+13,5+2*36*60/50+0,5+1=88,5 мин.;
2. Па = 2,36 м 3 /ч
3. Па = 2,74 м 3 /ч
4. Па = 3,80 м 3 /ч
5. Па = 9,27 м 3 /ч
Таблица 15.
| Грузоподъемность автосамосвала, т |
Tцикла , мин. |
Требуемое количество машин ( m) | |
| 6 | 77,2 | 29 | 29 |
| 7 | 77,5 | 26 | 31 |
| 10 | 79,8 | 17 | 22 |
| 27 | 88,5 | 7 | 13 |
В таблице 8 приведены результаты расчетов по семейству автосамосвалов q* = {6; 7; 10; 27} для маршрута Е1 Е11 длиной 25 км .
Таблица 16
| Грузоподъемность автосамосвала, т |
Tцикла , мин. |
Требуемое количество машин ( m) | |
| 6 | 65,2 | 24 | 25 |
| 7 | 65,5 | 22 | 26 |
| 10 | 67,8 | 14 | 19 |
| 27 | 76,5 | 6 | 11 |
T ц 6 =1,5+2,7+2*40*60/50+0,5+0,5= 65,2мин.;
T ц 7 =1,5+3+2*40*60/50+0,5+0,5=65,5 мин.;
T ц 10 =1,5+4,8+2*40*60/50+0,5+1=67,8 мин.;
T ц 27 =1,5+13,5+2*40*60/50+0,5+1= 76,5мин.;
2. Па = 2,80 м 3 /ч
3. Па = 3,24 м 3 /ч
4. Па = 4,48 м 3 /ч
5. Па = 10,72 м 3 /ч
Необходимое количество автосамосвалов для каждого комплекта машин и для каждого маршрута рассчитывается по формулам (1) и (2).
Среднее количество машин по двум лучам определяется по формуле:
![]()
где m1 и m2 — рассчитанное количество автосамосвалов по каждому лучу;
- tц1, tц2 — рассчитанная продолжительность циклов автосамосвалов по каждому лучу.
Таблица . Количество автосамосвалов, необходимых для маршрутов Е1-Е10 и Е1 — Е11.
| Маршрут | Грузоподъемность автосамосвала,т | Количество автосамосвалов(m1) | Количество автосамосвалов(m2) | Максимальное количество автосамосвалов |
| Е1-Е10 | 6 | 29 | 29 | 29 |
| 7 | 26 | 31 | 31 | |
| 10 | 16 | 22 | 22 | |
| 27 | 7 | 13 | 13 | |
| Е1-Е11 | 6 | 24 | 25 | 25 |
| 7 | 22 | 26 | 26 | |
| 10 | 14 | 19 | 19 | |
| 27 | 6 | 11 | 11 |
Целесообразно использовать автосамосвалы с грузоподъемностью 10 и 27 тонн.
m ср1 =(22*79,8+19*67,8)/(79,8+67,8)=21
m ср2 =(13*88,5+11*76,5)/(88,5+76,5)=12
m ср1 =(22*79,8+11*76,5)/(79,8+76,5)=17
m ср1 =(13*88,5+19*67,8)/(88,5+67,8)=16
Далее максимальное число автосамосвалов распределяется по двум лучам по формулам:
- m1″=tц1/tц1+tц2;
- m2″=tц2/tц1+tц2;
— Суммарная производительностьсистемы представлена в таблице.
| № | Е1-Е10 | Е1-Е11 | Для всей системы: | ||
| m1″ | m1″*Па | m2″ | m2″*Па | m1″*Па+m2″*Па | |
| 1 | 12 | 45,6 | 9 | 162,12 | 207,72 |
| 2 | 6 | 22,8 | 6 | 96,94 | 119,94 |
| 3 | 9 | 34,2 | 8 | 85,76 | 119,96 |
| 4 | 9 | 96,48 | 7 | 26,6 | 123,08 |
Выбирается тот комплект машин, который обеспечивает максимальную производительность, в пределах условия m1″*Па+m2″*Па>Пэ на 20%. Этому условию удовлетворяет вариант
Экскаватор с объемом ковша 1,00
12 автосамосвалов грузоподъемностью 10 т на маршрут Е1-Е10;
9автосамосвалов грузоподъемностью 10 т на маршрут Е1-Е11;
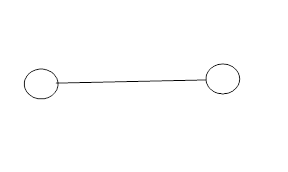
Cij*=Cij, если 0<xij<bij;
![]()
Схема 4. Пропускные способности сети.
Пропускные способности отдельных участков сети определяются исходя из рассчитанной выше суммарной производительности потоков автосамосвалов, идущих по этим участкам сети.
Пропускная способность вычисляется по формуле:
b ij =mik *Па ik *kа,
где bij — пропускная способность по ребру между двумя пунктами, м 3 /час
к — число маршрутов;
- ka — коэффициент перевыполнения (1,15-1,20);
- Пропускная способность ребер, через которые одновременно проходят несколько маршрутов, представляет собой сумму пропускных способностей каждого из этих маршрутов.
Ниже представлен список маршрутов и соответствующих им пропускных способностей.
Е 1 Е10 -55м3 /час
Е 1 Е11 — 48м3 /час
Е 2 Е10 — 95,4м3 /час
Е 3 Е11 — 180м3 /час
Транспортная сеть с нанесенными на ней пропускными способностями и стоимостями перевозок представлена на схеме 3..
Постановка задачи: задана сеть с одним истоком Е 0 и одним стоком Е12 , и промежуточными вершинами Е1 -Е11 . Каждому ребру поставлены в соответствие две величины: пропускная способность bij и дуговая стоимость Cij (стоимость доставки единицы потока по ребру Еij).
Необходимо найти поток из источника в сток заданной величины В, обладающий минимальной стоимостью.
Целевая функция:
F = ![]() ® min
® min
Ограничения:
0£x £ bij, i ¹ j, i,j = 0,n
![]() — закон сохранения потока
— закон сохранения потока
![]() — поток, идущий из источника, равен потоку, входящему в сток, и равен максимальному потоку в сети.
— поток, идущий из источника, равен потоку, входящему в сток, и равен максимальному потоку в сети.
При наличии ограничений на пропускные способности ребер можно последовательно находить различные пути минимальной стоимости и пропускать по ним поток до тех пор, пока суммарная величина потока по всем путям не будет равна заданной величине потока.
Алгоритм Басакера-Гоуэна
Положим все дуговые потоки равными нулю (Xij=0).
Находим в сети путь с минимальной стоимостью и определяем модифицированные дуговые стоимости Cij, зависящие от величины найденного потока следующим образом:
С * ij = Cij , если 0£xij £ bij , и С* ij =¥, если xij =bij .
Ход решения задачи:
1. Выбираем путь с минимальной стоимостью. Это маршрут Е1Е11. Максимальная величина потока, равная минимальной пропускной способности, равна v1 =48 м3 /час. С1=5,28.Q1=min(bij)=min(103;48)=48. Х111=49. Закрываем дугу Е9-Е11.
2. Выбираем путь с минимальной стоимостью. Это маршрут Е3 — Е11. Максимальная величина потока, равная минимальной пропускной способности, равна v2=180 м3 /час. С1=5,28.Q1=min(bij)=min(180;180)=180. Х311=180. Закрываем дуги Е3-Е4,Е4-Е11.
3. Выбираем путь с минимальной стоимостью. Это маршрут Е1 — Е10. Максимальная величина потока, равная минимальной пропускной способности, равна v3=55 м3 /час. С1=6,08.Q1=min(bij)=min(55;55)=180. Х110=55. Закрываем дуги Е1-Е9,Е9-Е10.
4. Выбираем путь с минимальной стоимостью. Это маршрут Е2 — Е10. Максимальная величина потока, равная минимальной пропускной способности, равна v4=95 м3 /час. С1=6,11. Q1=min(bij)=min(95;95)=95. Х210=55. Закрываем дуги Е2-Е5,Е5-Е6, Е6-Е10.
Все ребра закрыты, задача решена.
Пропускные способности каждого ребра:
| Маршрут | bij, м 3 /час |
| Е1-Е9 | 103 |
| Е9-Е10 | 55 |
| Е9-Е11 | 48 |
| Е2-Е5 | 95 |
| Е5-Е6 | 95 |
| Е6-Е10 | 95 |
| Е3-Е4 | 180 |
| Е4-Е11 | 180 |
Суммарный поток равен сумме всех потоков, проходящих через сечение (см. чертеж).
V=Sv i = 378 м3 /час.
Время выполнения данного объема перевозок:
- t = V/m*Па;
- где — t — время;
- V — объем перевозок;
- m*Па — производительность системы;
Е 1 Е10 — 942,5час
Е 1 Е11 — 124час
Е 2 Е10 — 276,72час
Е 3 Е11 — 558,03час
Почасовые графики перевозки нерудных материалов приведены в Приложении.
Изучение спроса на транспортные услуги свидетельствует, что важнейшим требованием клиентов к работе автомобильного транспорта является своевременность отправки и доставки грузов. Вызвано это стремлением многих грузовладельцев к сокращению запасов в производстве и в потреблении, поскольку их затраты на содержание запасов по ряду отраслей составляют более 20% на единицу выпускаемой продукции.
Это доказывает важность решения задачи оптимального управления движением потоков грузов. Оптимальность в данном случае выражается в том, что доставка грузов происходит точно в срок и при минимальных затратах на перевозку. Решить эту сложную комплексную задачу позволяют некоторые методы исследования операций, а также теоретические разработки логистической теории.
В настоящее время, при переходе к рыночной экономике, задача минимизации расходов на транспортировку и распространение продукции становится одной из основных задач каждого предприятия, так как успешное ее решение позволяет существенно снизить издержки на изготовление продукции и тем самым повысить прибыльность предприятия.
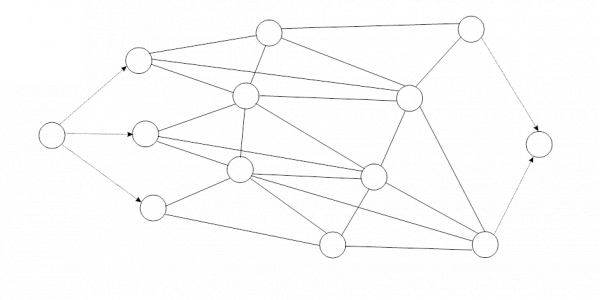
Схема 3. » Определение потока минимальной стоимости».
1. Яблонский А.А. Моделирование систем управления строительными процессами: Монография. — Москва, 1994. — Федеральная целевая программа книгоиздания России, — 296 с
2. Яблонский А.А., Тризина В.А. Управление потоком автосамосвалов, транспортирующих грунт экскаватора на два участка автодороги: Изв. Вузов.-1991. — №12. — с. 94-98.
3. Кофман А. Методы и модели исследования операций. — М.,Мир, 1996. — 523с.