Исторически геометрия начиналась с треугольника, поэтому вот уже два с половиной тысячелетия треугольник является как бы символом геометрии; но он не только символ, он — атом геометрии.
Почему именно треугольник можно считать атомом геометрии? Потому что предшествующие понятия — точка, прямая и угол — это неясные и неосязаемые абстракции вместе со связанным с ними набором теорем и задач. Поэтому сегодня школьная геометрия только тогда может стать интересной и содержательной, только тогда может стать собственно геометрией, когда в ней появляется глубокое и всестороннее изучение треугольника.
Удивительно, но треугольник, несмотря на свою кажущуюся простоту, является неисчерпаемым объектом изучения — никто даже в наше время не осмелится сказать, что изучил и знает все свойства треугольника.
Значит, изучение школьной геометрии не может осуществляться без глубокого изучения геометрии треугольника; ввиду многообразия треугольника как объекта изучения — а, значит, и источника различных методик его изучения — необходимо подбирать и разрабатывать материал для изучения геометрии замечательных точек треугольника. Причем при подборе этого материала не следует ограничиваться только лишь замечательными точками, предусмотренными в школьной программе Государственным образовательным стандартом, такими как центр вписанной окружности (точка пересечения биссектрис), центр описанной окружности (точка пересечения серединных перпендикуляров), точка пересечения медиан, точка пересечения высот. Но для глубокого проникновения в природу треугольника и постижения его неисчерпаемости необходимо иметь представления как можно о большем числе замечательных точек треугольника. Помимо неисчерпаемости треугольника как геометрического объекта, необходимо отметить удивительнейшее свойство треугольника как объекта изучения: изучение геометрии треугольника можно начинать с изучения любого его свойства, взяв его за основу; затем методику изучения треугольника можно построить так, чтобы на эту основу нанизывать все остальные свойства треугольника. Другими словами, с чего бы ни начинать изучение треугольника, всегда можно дойти до любых глубин этой удивительной фигуры. Но тогда — как вариант — можно начинать изучение треугольника с изучения его замечательных точек.
Цель курсовой работы состоит в изучении замечательных точек треугольника. Для достижения поставленной цели необходимо решить следующие задачи:
- Изучить понятия биссектрисы, медианы, высоты, серединного перпендикуляра и их свойства.
- Рассмотреть точку Жергонна, окружность Эйлера и прямую Эйлера, не изучаемые в школе.
1 Центр вписанной окружности треугольника
Замечательные точки треугольника — точки, местоположение которых однозначно определяется треугольником и не зависит от того, в каком порядке берутся стороны и вершины треугольника.
Измерения геометрических величин в курсе геометрии 7-9 классов
... треугольника, координатный метод, метод геометрических мест [16]. Далее мы рассмотрим, с какими измерительными следует знакомить школьников, и как эти инструменты могут помочь в изучении геометрии. §4. Измерительные в школе Измерения ... являются не только неотъемлемой частью процесса обучения математике в школе, но и ...
Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противоположной стороне.
Теорема. Каждая точка биссектрисы неразвернутого угла равноудалена (т.е. равноудалена от прямых, содержащих стороны треугольника) от его сторон. Обратно: каждая точка, лежащая внутри угла и равноудаленная от сторон угла, лежит на его биссектрисе.
Доказательство. 1) Возьмем произвольную точку М на биссектрисе угла ВАС, проведем перпендикуляры МК и МL к прямым АВ и АС и докажем, что МК=МL. Рассмотрим прямоугольные треугольники ΔАМК и ΔАМL. Они равны по гипотенузе и острому углу (АМ — общая гипотенуза, 1 = 2 по условию).
Следовательно, МК=МL.
Пусть точка М лежит внутри ВАС и равноудалена от его сторон АВ и АС. Докажем, что луч АМ — биссектриса ВАС. Проведем перпендикуляры МК и МL к прямым АВ и АС. Прямоугольные треугольники АКМ и АLM равны по гипотенузе и катету (АМ — общая гипотенуза, МК=МL по условию).
Следовательно, 1 = 2. Но это и означает, что луч АМ — биссектриса ВАС. Теорема доказана.
Следствие. Биссектрисы треугольника пересекаются в одной точке, (центр вписанной окружности, и центр).
Обозначим буквой О точку пересечения биссектрис АА1 и ВВ1 треугольника АВС и проведем из этой точки перпендикуляры ОК, ОL и ОM соответственно к прямым АВ, ВС и СА. По теореме (Каждая точка биссектрисы неразвернутого угла равноудалена от его сторон. Обратно: каждая точка, лежащая внутри угла и равноудаленная от сторон угла, лежит на его биссектрисе) мы говорим о том, что ОК = ОМ и ОК = OL. Поэтому OM = OL, т е точка O равноудалена от сторон АСВ и, значит лежит на биссектрисе СС1 этого угла. Следовательно, все три биссектрисы ΔАВС пересекаются в точке О, что и требовалось доказать.
окружность биссектриса треугольник прямая
1.2 Свойства биссектрисы треугольника
Биссектриса BD (рис. 1.1) любого угла ΔABC делит противоположную сторону на части AD и CD, пропорциональные прилежащим сторонам треугольника.
Требуется доказать, что если ABD = DBC, то AD : DC =АВ : ВС.
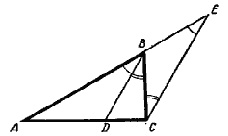
Рис.1.1
Проведём СЕ || BD до пересечения в точке Е с продолжением стороны АВ. Тогда, согласно теореме о пропорциональности отрезков, образующихся на прямых, пересечённых несколькими параллельными прямыми, будем иметь пропорцию: AD : DC = АВ: BE. Чтобы от этой пропорции перейти к той, которую требуется доказать, достаточно обнаружить, что ВЕ = ВС, т. е. что ΔВСЕ равнобедренный. В этом треугольнике Е =ABD (как углы соответственные при параллельных прямых) и ВСЕ = DBC (как углы накрест лежащие при тех же параллельных прямых).
Но ABD = DBC по условию; значит, Е = ВСЕ, а потому равны и стороны BE и ВС, лежащие против равных углов.
История измерения углов
... части. Градус является наиболее распространенной единицей измерения углов. Определение 2. Углом в 1 радиан называется центральный угол, опирающийся на дугу окружности, имеющую длину, ... трисекция угла), история ее происхождения. Построение трисектрисы угла (лучей, делящих угол) с помощью циркуля и линейки. Общее доказательство о трисекции угла, зависимость между ней и антипараллелограммом. реферат ...
Теперь, заменив в написанной выше пропорции BE на ВС, получим ту пропорцию, которую требуется доказать.
20 Биссектрисы внутреннего и смежного с ним угла треугольника перпендикулярны.
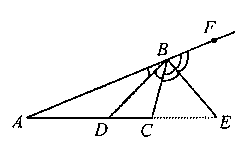
Рис. 1.2
Доказательство. Пусть BD — биссектриса ABC (рис.1.2), а BE — биссектриса смежного с указанным внутренним углом внешнего CBF, ΔABC. Тогда если обозначить ABD = DBC = α, CBE = EBF = β, то 2α + 2β= 1800 и, таким образом, α+ β = 900. А это и означает, что BD⊥ BE.
30 Биссектриса внешнего угла треугольника делит противолежащую сторону внешним образом на части, пропорциональные прилежащим сторонам.
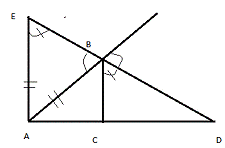
Рис.1.3
(Рис.1.3) AB: BC = AD: DC, ΔAED ~ ΔCBD, AE/BC = AD/DC = AE/BC.
40 Биссектриса любого угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника.
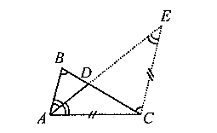
Рис. 1.4
Доказательство. Рассмотрим ΔABC. Пусть для определенности биссектриса CAB пересекает сторону BC в точке D (рис.1.4).
Покажем, что BD: DC = AB: AC. Для этого проведем через точку C прямую, параллельную прямой AB, и обозначим через E точку пересечения этой прямой AD. Тогда DAB=DEC, ABD=ECD и поэтому ΔDAB ~ ΔDEC по первому признаку подобия треугольников. Далее, так как луч AD — биссектриса CAD , то CAE = EAB = AEC и, значит, ΔECA равнобедренный. Отсюда AC=CE. Но в таком случае из подобия ΔDAB и ΔDEC следует, что BD: DC=AB: CE =AB: AC, а это и требовалось доказать.
Если биссектриса внешнего угла треугольника пересекает продолжение стороны, противолежащей вершине этого угла, то отрезки от полученной точки пересечения до концов противолежащей стороны пропорциональны прилежащим сторонам треугольника.
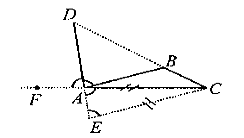
Рис. 1.5
Доказательство. Рассмотрим ΔABC. Пусть F — точка на продолжении стороны CA, D — точка пересечения биссектрисы внешнего BAF треугольника с продолжением стороны CB (рис. 1.5).
Покажем, что DC:DB=AC:AB. Действительно, проведем через точку C прямую, параллельную прямой AB, и обозначим через E точку пересечения этой прямой с прямой DA. Тогда треугольник ADB ~ ΔEDC и, значит, DC:DB=EC:AB. А поскольку ∠EAC= ∠BAD= ∠CEA, то в равнобедренном ΔCEA сторона AC=EC и, таким образом, DC:DB=AC:AB, что и требовалось доказать.
3 Решение задач на применение свойств биссектрисы
Задача 1. Пусть O — центр окружности, вписанной в ΔABC, CAB = α. Доказать, что COB = 900 + α/2.
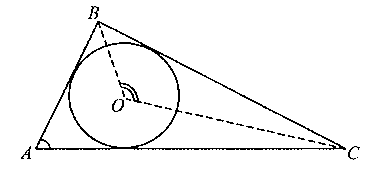
Рис. 1.6
Решение. Так как O — центр вписанной в ΔABC окружности (рис 1.6), то лучи BO и CO — биссектрисы ABC и BCA соответственно. А тогда COB = 1800 — (OBC +BCO)= 1800 — (ABC + BCA)/2 = 1800 -( 1800 — α)/2 = 900 + α/2, что и требовалось доказать.
Сборка объективов насыпной конструкции Расчет автоколлимационных точек
... прямой липни, называемой оптической осью системы. В зависимости от точности центрирования линз различают следующие основные типы объективов. 1. Объективы «насыпной» конструкции, в которых линзы в оправах ... работу объектива в реальных условиях эксплуатации; выпуск необходимого количества объективов в установленные сроки. сборки объектива ... вращении шпинделя описывают окружности. Смещения центров кривизны ...
Задача 2. Пусть O — центр описанной около ΔABC окружности, H — основание высоты, проведенной к стороне BC. Доказать, что биссектриса CAB является также и биссектрисой ∠OAH.
Решение.
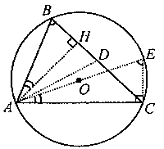
Рис. 1.7
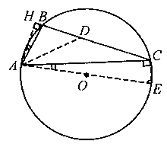
Рис.1.8
Пусть AD — биссектриса CAB, AE — диаметр описанной около ΔABC окружности (рис.1.7,1.8).
Если ΔABC — остроугольный (рис. 1.7) и, значит, ABC<900, то так как ABC = AEC= ½ дуги AC, а ΔBHA и ΔECA прямоугольные (BHA =ECA = 900 ), то ΔBHA ~ ΔECA и, следовательно, CAO = CAE =HAB. Далее, BAD и CAD равны по условию, поэтому HAD = BAD — BAH =CAD — CAE = EAD = OAD. Пусть теперь ABC = 900 . В этом случае высота AH совпадает со стороной AB, то точка O будет принадлежать гипотенузе AC и поэтому справедливость утверждения задачи очевидна.
Рассмотрим случай, когда ABC > 900 (рис.1.8).
Здесь четырехугольник ABCE вписан в окружность и, следовательно, AEC = 1800 — ABC. С другой стороны, ABH = 1800 — ABC, т.е. AEC = ABH. А поскольку ΔBHA и ΔECA — прямоугольные и, значит, HAB = 900 — ABH = 900 — AEC = EAC, то HAD = HAB +BAD = EAC + CAD = EAD = OAD. Случаи, когда BAC и ACB — тупые рассматриваются аналогично. ⊥
4 Точка Жергонна
Точкой Жергонна называется точка пересечения отрезков, которые соединяют вершины треугольника с точками касания сторон, противоположных этим вершинам, и вписанной в треугольник окружности.
Пусть точка O — центр вписанной окружности треугольника ABC. Пусть вписанная окружность касается сторон треугольника BC,AC и AB в точках D,E и F соответственно. Точка Жергонна — это точка пересечения отрезков AD, BE и CF. Пусть точка O — центр вписанной окружности ΔABC. Пусть вписанная окружность касается сторон треугольника BC, AC и AB в точках D, E и F соответственно. Точка Жергонна — это точка пересечения отрезков AD, BE и CF.
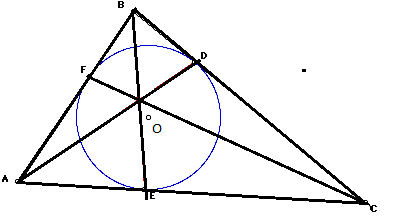
Рис.1.9
Докажем, что эти три отрезка действительно пересекаются в одной точке. Заметим, что центр вписанной окружности — это точка пересечения биссектрис углов ΔABC, а радиусы вписанной окружности OD, OE и OF ⊥ сторонам треугольника. Тем самым, имеем три пары равных треугольников (AFO и AEO, BFO и BDO, CDO и CEO).
Рис.1.10
Произведения AF·BD · CE и AE · BE · CF равны, поскольку BF = BD, CD = CE, AE = AF, следовательно, отношение этих произведений равно , и по теореме Чевы (Пусть точки A1, B1, С1 лежат на сторонах BC, AC и AB ΔABC соответственно. Пусть отрезки AA1, BB1 и CC1 пересекаются в одной точке. Тогда
(обходим треугольник по часовой стрелке)), отрезки пересекаются в одной точке.
Свойства вписанной окружности:
Окружность называется вписанной в треугольник, если она касается всех его сторон.
Использование методов подобия и анализа размерностей в компьютерном ...
... величин. Это простое соображение является основой дисциплины, известной как анализ размерностей (Баренблатт). Основой анализа размерностей является так называемая π-теорема. Грубо говоря, эта теорема утверждает, ... выполнении преобразований, а также содержательная интуиция являются здесь существенными элементами. Анализ размерностей позволяет нам понять размерностные (то есть связанные с длиной, ...
В любой треугольник можно вписать окружность.
Дано: ABC — данный треугольник, О — точка пересечения биссектрис, М, L и К — точки касания окружности со сторонами треугольника (рис. 1.11).
Доказать: О — центр окружности, вписанной в АВС.
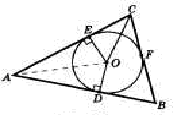
Рис.1.11
Доказательство. Проведем из точки О перпендикуляры OK, OL и ОМ соответственно к сторонам АВ, ВС и СА (рис.1.11).
Так как точка О равноудалена от сторон треугольника ABC, то ОК = OL = ОМ. Поэтому окружность с центром О радиуса ОК проходит через точки K, L, M. Стороны треугольника ABC касаются этой окружности в точках К, L, М, так как они перпендикулярны к радиусам ОК, OL и ОМ. Значит, окружность с центром О радиуса ОК является вписанной в треугольник ABC. Теорема доказана.
Центр окружности, вписанной в треугольник, является точкой пересечения его биссектрис.
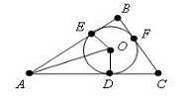
Рис.1.12
Пусть ABC данный, O — центр вписанной в него окружности, D, E и F — точки касания окружности со сторонами (рис.1.12).
Δ AEO = Δ AOD по гипотенузе и катету (EO = OD — как радиус, AO — общая).
Из равенства треугольников следует, что ∠ OAD = ∠ OAE. Значит AO биссектриса угла EAD. Точно также доказывается, что точка O лежит на двух других биссектрисах треугольника.
Радиус, проведенный в точку касания, перпендикулярен касательной.
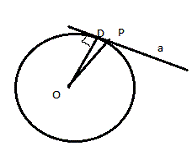
Рис.1.13
Доказательство. Пусть окр.(O; R) данная окружность (рис.1.13), прямая a касается ее в точке P . Пусть радиус OP не перпендикулярен к a . Проведем из точки O перпендикуляр OD к касательной. По определению касательной, все ее точки, отличные от точки P , и, в частности, точка D лежат вне окружности. Следовательно, длина перпендикуляра OD больше R длины наклонной OP . Это противоречит свойству наклонной, и полученное противоречие доказывает утверждение.
ГЛАВА 2. 3 замечательные точки треугольника, окружность Эйлера, прямая Эйлера.
1 Центр описанной окружности треугольника
Серединным перпендикуляром к отрезку называется прямая, проходящая через середину отрезка и перпендикулярная к нему.
Теорема. Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. Обратно: каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.
Доказательство. Пусть прямая m — серединный перпендикуляр к отрезку АВ, точка О — середина отрезка.
Рассмотрим произвольную точку М прямой m и докажем, что АМ=ВМ. Если точка М совпадает с точкой О, то это равенство верно, так как О — середина отрезка АВ. Пусть М и О — различные точки. Прямоугольные ΔОАМ и ΔОВМ равны по двум катетам (ОА=ОВ, ОМ — общий катет), поэтому АМ=ВМ.
Рассмотрим произвольную точку N, равноудаленную от концов отрезка АВ, и докажем, что точка N лежит на прямой m. Если N — точка прямой АВ, то она совпадает с серединой О отрезка АВ и поэтому лежит на прямой m. Если точка N не лежит на прямой АВ, то рассмотрим ΔАNB, который равнобедренный, так как АN=BN. Отрезок NO — медиана этого треугольника, а следовательно, и высота. Таким образом, NO перпендикулярна АВ, поэтому прямые ON и m совпадают, и, значит, N — точка прямой m. Теорема доказана.
Разработка логической игры «Точки»
... Го — настольная логическая игра. Как и в шахматах, в ней все зависит от способности игрока предвидеть ход игры, составить и воплотить ... и его нельзя рассматривать как серьезную систему для разработки современных приложений. Более того. Basic считается языком для ... курсового проекта состоит в том что бы реализовать игру «Точки» на любом из объектно-ориентированных языков программирования. Актуальность ...
Следствие. Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке, (центр описанной окружности).
Обозначим О, точку пересечения серединных перпендикуляров m и n к сторонам АВ и ВС ΔАВС. По теореме (каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. Обратно: каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.) мы делаем вывод что ОВ=ОА и ОВ=ОC поэтому: ОА=ОС, т е точка О равноудалена от концов отрезка АС и, значит, лежит на серединном перпендикуляре p к этому отрезку. Следовательно, все три серединных перпендикуляра m, n и p к сторонам ΔАВС пересекаются в точке О.
У остроугольного треугольника эта точка лежит внутри, у тупоугольного — вне треугольника, у прямоугольного — на середине гипотенузы.
Свойство серединного перпендикуляра треугольника:
Прямые, на которых лежат биссектрисы внутреннего и внешнего углов треугольника, выходящие из одной вершины, пересекаются с серединным к противолежащей стороне перпендикуляром с диаметрально противоположных точках описанной около треугольника окружности.
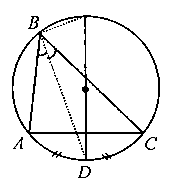
Рис. 2.1
Доказательство. Пусть, например, биссектриса ABC пересекает описанную около ΔABC окружность в точке D (рис. 2.1).
Тогда так как вписанные ABD и DBC равны, то AD= дуге DC. Но серединный к стороне AC перпендикуляр также делит дугу AC пополам, поэтому точка D будет принадлежать и этому серединному перпендикуляру. Далее, поскольку по свойству 30 из пункта 1.3 биссектриса BD ABC , смежного с ABC, то последняя пересечет окружность в точке, диаметрально противоположной точке D, так как вписанный прямой угол всегда опирается на диаметр.
2 Ортоцентр окружности треугольника
Высота — перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону.
Высоты треугольника (или их продолжения) пересекаются в одной точке, (ортоцентр).
Доказательство. Рассмотрим произвольный ΔАВС и докажем, что прямые АА1, ВВ1, СС1, содержащие его высоты, пересекаются в одной точке. Проведем через каждую вершину ΔАВС прямую, параллельную противоположной стороне. Получим ΔА2B2C2. Точки А, B и С являются серединными сторон этого треугольника. Действительно, АВ=А2C и АВ=СВ2 как противоположные стороны параллелограммов АВА2C и АВСВ2, поэтому А2C=СВ2. Аналогично С2A=АВ2 и С2B=ВА2. Кроме того, как следует из построения, СС1 перпендикулярен А2B2, АА1 перпендикулярен В2C2 и ВВ1 перпендикулярен А2C2. Таким образом, прямые АА1,ВВ1 и СС1 являются серединными перпендикулярами к сторонам ΔА2B2C2. Следовательно, они пересекаются в одной точке.
В зависимости от вида треугольника ортоцентр может находиться внутри треугольника в остроугольных, вне его — в тупоугольных или совпадать с вершиной, в прямоугольных — совпадает с вершиной при прямом угле.
Основы теории подобия (метод обобщенных переменных)
... в точке В — в момент времени τв . В геометрически подобной модели сходственная частица находится в подобной точке а в момент времени τа , в точке b— в момент времени τ b . Рис. 1. Условия подобия в натуре (a) и в ... положения теории подобия (теоремы подобия) Основные положения теории подобия заключены в теоремах подобия, которые лежат в основе практического применения теории подобия. подобные явления ...
Свойства высоты треугольника:
Отрезок, соединяющий основания двух высот остроугольного треугольника, отсекает от него треугольник, подобный данному, с коэффициентом подобия равным косинусу общего угла.
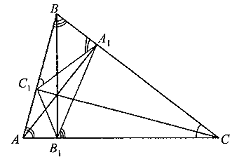
Рис. 2.2
Доказательство. Пусть AA1, BB1 , CC1 — высоты остроугольного треугольника ABC, а ABC = β (рис. 2.2).
Прямоугольные треугольники BA1A и CC1B имеют общий β, поэтому они подобны, а значит, BA1/BA = BC1/BC = cos β. Отсюда следует, что BA1/BC1=BA/BC = cos β, т.е. в ΔC1BA1 и ΔABC стороны, прилежащие к общему β, пропорциональны. А тогда по второму признаку подобия треугольников ΔC1BA1 ~ ΔABC, причем коэффициент подобия равен cos β. Аналогичным образом доказывается, что ΔA1CB1 ~ ΔABC с коэффициентом подобия cos BCA, а ΔB1AC1 ~ ΔABC с коэффициентом подобия cos CAB.
Высота, опущенная на гипотенузу прямоугольного треугольника, делит его на два подобных между собой и подобных исходному треугольнику, треугольника.
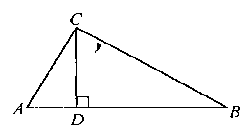
Рис. 2.3
Доказательство. Рассмотрим прямоугольный ΔABC, у которого ∠BCA = 900 , а CD — его высота (рис. 2.3).
Тогда подобие ΔADC и ΔBDC следует, например, из признака подобия прямоугольных треугольников по пропорциональности двух катетов, поскольку AD/CD = CD/DB. Каждый же из прямоугольных треугольников ADC и BDC подобен исходному прямоугольному треугольнику уже хотя бы на основании признака подобия по двум углам.
Решение задач на применение свойств высот
Задача 1. Доказать, что треугольник, одной из вершин которого является вершина данного тупоугольного треугольника, а две другие вершины — это основания высот тупоугольного треугольника, опущенных из двух других его вершин, подобен данному треугольнику с коэффициентом подобия, равным модулю косинуса угла при первой вершине.
Решение. Рассмотрим тупоугольный ΔABC с тупым CAB. Пусть AA1, BB1, CC1 — его высоты (рис. 2.4, 2.5, 2.6) и пусть CAB = α, ABC = β, BCA = γ.
Доказательство того факта, что ΔC1BA1 ~ ΔABC (рис.2.4) с коэффициентом подобия k = cosβ, полностью повторяет рассуждения, проведенные при доказательстве свойства 1, пункта 2.2.
Докажем, что ΔA1CB ~ ΔABC (рис. 2.5) с коэффициентом подобия k1= cos γ, а ΔB1AC1 ~ ΔABC (рис. 2.6) с коэффициентом подобия k2 = |cosα|.
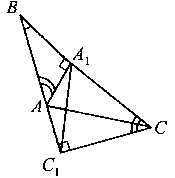
Рис. 2.4
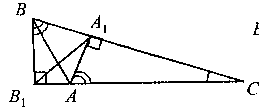
Рис. 2.5
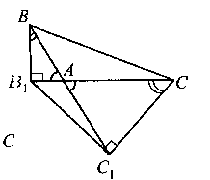
Рис. 2.6
Действительно, прямоугольные треугольники CA1A и CB1B имеют общий угол γ и поэтому подобны. Отсюда следует, что B1C/ BC = A1C / AC= cos γ и, значит, B1C/ A1C = BC / AC = cos γ, т.е. в треугольниках A1CB1 и ABC стороны, образующие общий ∠γ, пропорциональны. А тогда по второму признаку подобия треугольников ΔA1CB ~ ΔABC, причем коэффициент подобия k1= cos γ. Что же касается последнего случая (рис.2.6), то из рассмотрения прямоугольных треугольников ΔBB1A и ΔCC1A с равными вертикальными углами BAB1 и C1AC следует, что они подобны и, значит, B1A / BA = C1A / CA = cos (1800 — α) = |cosα|, так как ∠α — тупой. Отсюда B1A / C1A = BA /CA = |cosα| и, таким образом, в треугольниках ΔB1AC1 и ΔABC стороны, образующие равные углы, пропорциональны. А это означает, что ΔB1AC1 ~ ΔABC с коэффициентом подобия k2 = |cosα|.
Крым с экологической точки зрения
... К". Одно из перспективных направлений крымской пищевой промышленности - розлив натуральной минеральной воды. В Крыму отмечается значительное разнообразие минеральных вод - столовых, ... металлургический завод "Азовсталь" в Мариуполе. При переработке керченских руд получают также феррованадий. Промышленность строительных материалов в Крыму представлена разработанными производствами, базирующимися ...
Задача 2. Доказать, что если точка O — точка пересечения высот остроугольного треугольника ABC, то ABC + AOC = 1800, BCA + BOA = 1800, CAB + COB = 1800.
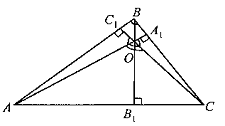
Рис.2.7
Решение. Докажем справедливость первой из приведенных в условии задачи формул. Справедливость остальных двух формул доказывается аналогично. Итак, пусть ABC = β, AOC =γ. A1, B1 и C1 — основания высот треугольника, проведенных из вершин A, B и C соответственно (рис.2.7).
Тогда из прямоугольного треугольника BC1C следует, что BCC1 = 900 — β и, таким образом, в прямоугольном треугольнике OA1C угол COA1 равен β. Но сумма углов AOC + COA1 =γ + β дает развернутый угол и поэтому AOC + COA1 = AOC + ABC = 1800, что и требовалось доказать.
Задача 3. Доказать, что высоты остроугольного треугольника являются биссектрисами углов треугольника, вершинами которого являются основания высот данного треугольника.
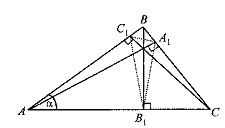ис.2.8
Решение. Пусть AA1, ВВ1, CC1 — высоты остроугольного треугольника ABC и пусть CAB = α (рис.2.8).
Докажем, например, что высота AA1 является биссектрисой угла C1A1B1. Действительно, так как треугольники C1BA1 и ABC подобны (свойство 1), то BA1C1 = α и, значит, C1A1A = 900 — α. Из подобия же треугольников A1CB1 и ABС следует, что AA1B1 = 900 — α и поэтому C1A1A = AA1B1= 900 — α. Но это и означает, что AA1 — биссектриса угла C1A1B1. Аналогично доказывается, что две другие высоты треугольника ABC являются биссектрисами двух других соответствующих углов треугольника A1B1C1.
3 Центр тяжести окружности треугольника
Медианой треугольника называется отрезок, соединяющий любую вершину треугольника с серединой противолежащей стороны.
Доказательство. Рассмотрим произвольный ΔАВС.
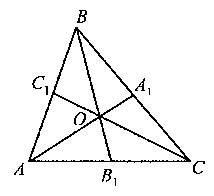
Рис. 2.9
Обозначим буквой О точку пересечения медиан АА1 и ВВ1 и проведем среднюю линию А1B1 этого треугольника. Отрезок А1B1 параллелен стороне АВ, поэтому 1 = 2 и 3 = 4. Следовательно, ΔАОВ и ΔА1ОВ1 подобны по двум углам, и, значит, их стороны пропорциональны: АО:А1O=ВО:В1O=АВ:А1B1. Но АВ=2А1B1, поэтому АО=2А1O и ВО=2В1O. Таким образом, точка О пересечения медиан АА1 и ВВ1 делит каждую из них в отношении 2:1,считая от вершины.
Аналогично доказывается, что точка пересечения медиан ВВ1 и СС1 делит каждую из них в отношении 2:1, считая от вершины, и, следовательно, совпадает с точкой О и делятся ею в отношении 2:1,считая от вершины.
Взаимосвязь науки и техники: основные точки зрения
... трудятся специалисты самых различных областей науки и техники. В силу этого координация всех ... схемы. Одной из наиболее важных, с точки зрения философии, особенностей современных научно-технических ... научно-технической проблемы. Однако несмотря на то, что на первый взгляд главной задачей здесь ... увидеть со стороны”, скорее можно ее почувствовать как нечто живое. Для постнеклассической науки в целом ...
Свойства медианы треугольника:
10 Медианы треугольника пересекаются в одной точке и делятся точкой пересечения в отношении 2:1, считая от вершины.
Дано: ΔАВС, АА1,ВВ1 — медианы.
Доказать: АО:ОА1=ВО:ОВ1=2:1
Доказательство. Проведем среднюю линию А1В1 (рис.2.10), по свойству средней линии А1В1||АВ, А1В1=1/2 AB. Так как А1В1 || АВ, то 1 = 2 накрест лежащие при параллельных прямых АВ и А1В1 и секущей АА1. 3 = 4 накрест лежащие при параллельных прямых А1В1 и АВ и секущей ВВ1.
Следовательно, ΔАОВ ~ ΔА1OB1 по равенству двух углов, значит, стороны пропорциональны: AO/A1O = OB/OB1 = AB/A1B = 2/1, AO/A1O = 2/1; OB/OB1 = 2/1.
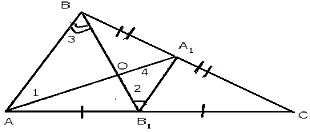
Рис.2.10
Медиана разбивает треугольник на два треугольника одинаковой площади.
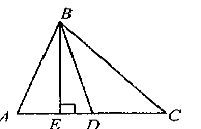
Рис.2.11
Доказательство. BD — медиана ΔABC (рис.2.11), BE — его высота. Тогда ΔABD и ΔDBC равновелики, так как они имеют равные основания AD и DC соответственно и общую высоту BE.
Весь треугольник разделяется своими медианами на шесть равновеликих треугольников.
Если на продолжении медианы треугольника отложить от середины стороны треугольника отрезок, равный по длине медиане, то концевая точка этого отрезка и вершины треугольника являются вершинами параллелограмма.
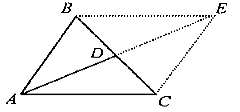
Рис. 2.12
Доказательство. Пусть D — середина стороны BC ΔABC (рис. 2.12), E — такая точка на прямой AD, что DE=AD. Тогда поскольку диагонали AE и BC четырехугольника ABEC в точке D их пересечения делятся пополам, то из свойства 13.4 и следует, что четырехугольник ABEC — параллелограмм.
Решение задач на применение свойств медиан:
Задача 1. Доказать, что если O — точка пересечения медиан ΔABC, то ΔAOB, ΔBOC и ΔAOC равновелики.
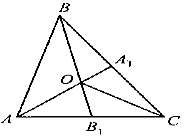
Рис.2.13
Решение. Пусть AA1 и BB1 — медианы ΔABC(рис. 2.13).
Рассмотрим ΔAOB и ΔBOC. Очевидно, что SΔAOB = SΔAB1B — SΔAB1O , SΔBOC = SΔBB1C — SΔOB1C . Но по свойству 2 имеем SΔAB1B = SΔBB1C , SΔAOB = SΔOB1C , откуда следует, что SΔAOB = SΔBOC . Аналогично доказывается и равенство SΔAOB = SΔAOC.
Задача 2. Доказать, что если точка O лежит внутри ΔABC и ΔAOB, ΔBOC и ΔAOC равновелики, то O — точка пересечения медиан ΔABC.
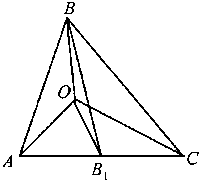
Рис. 2.14
Решение. Рассмотрим ΔABC (2.14) и предположим, что точка O не лежит на медиане BB1 . Тогда так как OB1 — медиана ΔAOC, то SΔAOB1 = SΔB1OC , а поскольку по условию SΔAOB = SΔBOC , то SΔAB1OB = SΔBOB1C . Но этого быть не может, так как SΔABB1 = SΔB1BC . Полученное противоречие означает, что точка O лежит на медиане BB1. Аналогично доказывается, что точка O принадлежит и двум другим медианам ΔABC. Отсюда и следует, что точка O действительно является точкой пересечения трех медиан ΔABC.
Задача 3. Доказать, что если в ΔABC стороны AB и BC не равны, то его биссектриса BD лежит между медианой BM и высотой BH.
Доказательство. Опишем около ΔABC окружность и продолжим его биссектрису BD до пересечения с окружностью в точке K. Через точку K будет проходить серединный к отрезку AC перпендикуляр (свойство1, из пункта 2.1), который с медианой имеет общую точку M. Но так как отрезки BH и MK параллельны, а точки B и K лежат по разные стороны от прямой AC, то точка пересечения отрезков BK и AC принадлежат отрезку HM, а это и доказывает требуемое.
Задача 4. В ΔABC медиана BM в два раза меньше стороны AB и образует с ней угол 400. Найдите ABC.
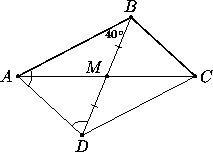
Рис 2.15
Решение. Продлим медиану BM за точку M на ее длину и получим точку D ( рис. 2.15).
Так как AB = 2BM , то AB = BD , то есть треугольник ABD — равнобедренный. Следовательно, BAD = BDA = (180o — 40o) : 2 = 70o. Четырёхугольник ABCD является параллелограммом, так как его диагонали точкой пересечения делятся пополам. Значит, CBD = ADB = 700 . Тогда ABC = ABD + CBD =1100.Ответ 1100.
Задача 5. Стороны ∆ABC равны a, b, c . Вычислить медиану mc, проведенную к стороне с.( рис.2.16 ).
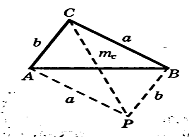
Рис.2.16
Решение. Удвоим медиану, достроив ∆ABC до параллелограмма АСВР, и применим к этому параллелограмму теорему 8. Получим: CP2+AB2 = 2AC2+2BC2, т.е. (2mc)2+c2= 2b2+2a2, откуда находим:
2.4 Окружность Эйлера. Прямая Эйлера
Теорема. Основания медиан, высот произвольного треугольника, а также середины отрезков, соединяющих вершины треугольника с его ортоцентром, лежат на одной окружности, радиус которой равен половине радиуса описанной около треугольника окружности. Эта окружность называется окружностью девяти точек или окружностью Эйлера.
Доказательство. Возьмем серединный ∆MNL (рис. 2.17) и опишем около него окружность W. Отрезок LQ — медиана в прямоугольном ∆AQB, поэтому LQ=1/2AB. Отрезок MN=1/2AB, т.к. MN- средняя линия ∆ABC. Отсюда следует, что трапеция QLMN — равнобочная. Так как окружность W проходит через 3 вершины равнобочной трапеции L, M, N, то она пройдет и через четвертую вершину Q. Аналогично доказывается, что P принадлежит W, R принадлежит W.
Перейдем к точкам X, Y, Z. Отрезок XL перпендикулярен BH как средняя линия ∆AHB. Отрезок BH перпендикулярен AC и так как AC параллельно LM, то BH перпендикулярно LM. Следовательно, XLM=П/2. Аналогично, XNM= П/2.
В четырехугольнике LXNM два противоположных угла прямые, поэтому около него можно описать окружность. Это будет окружность W. Итак, X принадлежит W, аналогично Y принадлежит W, Z принадлежит W.
Серединный ∆LMN подобен ∆ABC. Коэффициент подобия равен 2. Следовательно, радиус окружности девяти точек равен R/2.
Свойства окружности Эйлера:
Радиус окружности девяти точек равен половине радиуса окружности, описанной около ∆ABC.
Окружность девяти точек гомотетична окружности, описанной около ∆ABC, с коэффициентом ½ и центром гомотетии в точке H.
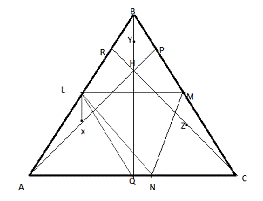
Рис. 2.18
Теорема. Ортоцентр, центроид, центр описанной окружности и центр окружности девяти точек лежат на одной прямой. Прямая Эйлера.
Доказательство. Пусть H — ортоцентр ∆ABC (рис.2.18) и O — центр описанной окружности. По построению серединные перпендикуляры ∆ABC содержат высоты серединного ∆MNL, т. O одновременно ортоцентром ∆LMN. ∆LMN ~ ∆ABC, их коэффициент подобия равен 2, поэтому BH=2ON.
Проведем через точки H и O прямую. Получим два подобных треугольника ∆NOG и ∆BHG. Так как BH=2ON, то и BG=2GN. Последнее означает что точка G является центроидом ∆ABC. Для точки G выполняется соотношение HG:GO=2:1.
Пусть далее TF есть серединный перпендикуляр ∆MNL и F — точка пересечения этого перпендикуляра с прямой HO. Рассмотрим подобные ∆TGF и ∆NGO. Точка G — центроид ∆MNL, поэтому коэффициент подобия ∆TGF и ∆NGO равен 2. Отсюда OG=2GF и так как HG=2GO, то HF=FO и F — середина отрезка HO.
Если провести те же рассуждения относительно серединного перпендикуляра к другой стороне ∆MNL, то он также должен пройти через середину отрезка HO. Но это означает, что точка F — точка серединных перпендикуляров ∆MNL. Такая точка является центром окружности Эйлера. Теорема доказана.
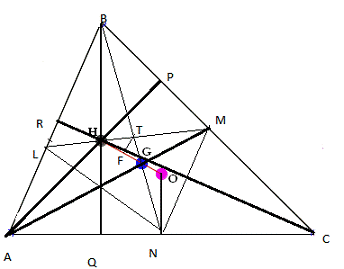
Рис.2.18
ЗАКЛЮЧЕНИЕ
В данной работе мы рассмотрели 4 замечательные точки треугольника, изучаемые в школе и их свойства, на основе которых мы можем решать множество задач. Так же были рассмотрены точка Жергонна, окружность Эйлера и прямая Эйлера.
1. Геометрия 7-9. Учебник для средних школ // Атанасян Л.С., Бутузов В.Ф. и др. — М.: Просвещение, 1994.
2. Амелькин В.В. Геометрия на плоскости: Теория, задачи, решения: Учеб. Пособие по математике // В. В. Амелькин, В.Л. Рабцевич, В.Л. Тимохович — Мн.: «Асар », 2003.
- В.С. Болодурин, О.А. Вахмянина, Т.С. Измайлова // Пособие по элементарной геометрии. Оренбург, ОГПИ, 1991.
- Прасолов В.Г.
Задачи по планиметрии. — 4-е изд., дополненное — М.: Изд-во Московского центра непрерывного математического обра-зования, 2001.
