Изгиб прямолинейного стержня

метки: Технический, Сечение, Механик, Изгибать, Стержень, Уравнение, Момент, Реакция

БЕЛОРУССКИЙ ГОСУДРАСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ

Кафедра инженерной графики

РЕФЕРАТ

На тему:

Изгиб прямолинейного стержня

МИНСК, 2008

Общие понятия о деформации изгиба

М _и

Если изгибающий момент в поперечном сечении является единственной составляющей внутренних сил, изгиб называется чистым.

М _и

М _и

Использование уравнений равновесия и возможно для систем сил, действующих на свободные тела

Формально несвободные изгибаемые стержни можно считать свободными используя принцип освобождаемости от связей. Согласно ему, любое несвободное тело можно представить свободным, отбросив ограничивающие его движение связи (опоры) и заменив их действие силами реакции этих связей . Уравнения равновесия и можно использовать для определения внутренних сил в поперечных сечениях изгибаемых стержней при условии, что помимо внешних сил будут учитываться и силы реакций опор. Поэтому прежде чем определить внутренние силы в поперечных сечениях изгибаемых стержней, нужно уметь находить величину и направление реакций опор. Известно, что реакция связи (опоры) направлена всегда в сторону, противоположную той, куда связь не дает перемещаться телу. Если связь препятствует поступательному движению тела, ее реакция – сила; если связь препятствует вращательному движению, ее реакция – момент сил.

Рис. 2

г

в

б

а

в

б

в

б

а

а

Рис. 3

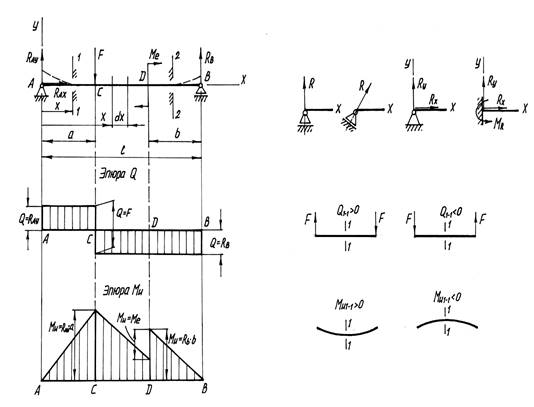
Рис. 1

Различают три основных типа опор стержней при изгибе.

Подвижная шарнирная опора, Неподвижная шарнирная опора, Жесткая заделка или защемление

Далее, «заменив» опоры силами их реакций, составляют уравнения равновесия для системы сил, действующей на изгибаемый стержень. Независимых уравнений равновесия для плоской системы сил три. Задача статически определима, если число неизвестных составляющих реакций опор не более трех.

Это возможно при следующих вариантах крепления изгибаемых стержней: защемление стержня одним концом (контактные пружины) или крепление стержня с помощью подвижной и неподвижной шарнирных опор (валы).

При большем количестве неизвестных составляющих реакций применяют иные, не рассматриваемые в пособии, способы решения.

Если при вычислении величину реакции опоры получили отрицательной , со знаком минус , то действительное направление реакции будет противоположно принятому , что обязательно нужно учитывать при определении внутренних сил.

Пример .

Определим реакции в опорах А и В изгибаемого стержня, схема нагружения (F, M_e ) и размеры (a, b, ℓ) которого представлены на рис. 1, а. Заменим подвижную опору В реакцией R_B , а неподвижную шарнирную опору А – составляющими R_AX и R_AY . «Свободный» стержень под действием внешних сил и сил реакций опор находится в покое. Отсутствие возможных составляющих плоского движения (поступательные перемещения вдоль осей x и y и вращательное движение в плоскости действия сил, т.е. вокруг оси z ) стержня выразим с помощью уравнений равновесия:

. (1)

R _B

Определение внутренних усилий при изгибе. Построение эпюр поперечных сил и изгибающих моментов

При плоском поперечном изгибе в поперечных сечениях стержня возникают следующие составляющие внутренних сил – поперечная сила Q и изгибающий момент М_и . Для их определения используют метод сечений.

Поперечная сила, Изгибающий момент

При определении Q и М _и используется скользящая система координат, когда отсчет сечений ведут либо от крайнего левого, либо от крайнего правого сечения стержня.

Для консольных жестко закрепленных с одной стороны (рис. 5.24, а) стержней поперечную силу и изгибающий момент удобнее определить без нахождения реакций опоры, рассматривая по отношению к сечению силы, действующие на незакрепленный участок стержня. Значения Q и М_и в точке закрепления В будут равны составляющим реакции опоры, т.е. Q_B = F = R_BY , М_{и B} = F·ℓ= M_RB .

Поперечная сила Q и изгибающий момент М_и в общем случае зависят от положения сечения по длине стержня, т.е. от величины х . Проверку условий прочности проводят в опасных наиболее нагруженных сечениях, в сечениях с наибольшими внутренними силами и максимальными напряжениями. Для нахождения опасных сечений и для наглядного представления о характере изменения внутренних сил строят графики распределения поперечных сил Q = Q (x) и изгибающего момента М_и = М_и (х) по длине стержня, т.е. эпюры поперечных сил и изгибающего момента .

Стержень разбивают на участки, на протяжении которых нагрузка однородна. Для эпюр Q и М_и проводят линии, параллельные продольной оси стержня. Границы участков сносят на эти линии. Для каждого участка составляют общие выражения величины поперечной силы Q = Q (x) и изгибающего момента М_и = М_и (х), для чего рассматривают произвольные сечения в пределах участка. Далее строят эпюры Q и М_и , задавая аргументу х значения в пределах каждого участка. Величины поперечной силы и изгибающего момента откладывают как ординаты эпюры в масштабе: Рассмотрим изменение τ для стержня прямоугольного сечения (рис. 5.23, б).

Статический момент заштрихованной площадки относительно нейтральной оси z равен

, где – расстояние от оси z до центра масс отсеченной части сечения. Это уравнение параболы. Касательные напряжения определим по формуле учитывая, что I_z = bh³ /12;

.

Эпюру касательных напряжений (рис. 5.23, в) строим по трем точкам: τ _{y = h /2} = τ_{y = – h /2} = 0; τ_{y = 0} = 1,5 (Q/A).

Наибольшие касательные напряжения в поперечном сечении действуют на уровне нейтральной оси. Для стержней прямоугольного сечения они в 1,5 раза больше того напряжения, которое получилось бы при равномерном распределении касательных напряжений по сечению.

Касательные напряжения при изгибе максимальны на нейтральной оси и при других формах поперечного сечения. Для стержней круглого поперечного сечения они равны τ _max = (4/3)(Q/A), для стержней кольцевого сечения – τ_max = 2(Q/A).

Условие прочности стержней при изгибе по касательным напряжениям имеет вид τ _max ≤ τ_adm , где τ _adm – допускаемое напряжение материала стержня на срез или сдвиг. Отметим, что касательные напряжения в поперечных сечениях изгибаемых стрежней много меньше нормальных, поэтому расчет на прочность ведут обычно по нормальным напряжениям в соответствии с выражением без учета влияния поперечных сил.

Определение деформаций при изгибе

перемещением у

а

в

д

г

б

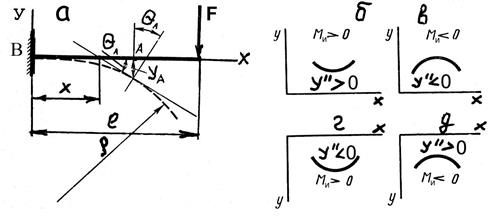
Рис. 4

Касательная к изогнутой оси стержня в любой ее точке составит с первоначальной осью угол, равный углу поворота θ сечения в данной точке. Тангенс угла θ наклона касательной tgθ = dy/dx. Но так как фактические значения углов поворота поперечных сечений при изгибе малы, порядка тысячных долей радиана, можно тангенс угла приравнять значению угла (tgθ ≈ θ) и найти связь между углом поворота сечения и прогибом в виде зависимости θ ≈ ≈ dy/dx.

Из курса математики известна следующая зависимость для кривизны K линии, расположенной в плоскости x0y:

. (2)

Но так как (dy/dx) ² = tg² θ = θ² << 1, то выражение (2) упростим, представив в виде

. (3)

М _и

K = 1/ρ = М _и /(EI_z ).

(4)

Сравнивая полученные выражения кривизны в зависимостях (3) и (4), получим дифференциальное уравнение изогнутой оси стержня:

, (5)

интегрирование которого не представляет затруднений. Выбор знака в выражении определяется принятой системой координат.

М _и

Кривизна линии положительная, т.е. y» = d ² y/dx² > 0, если вогнутость кривой совпадает с положительным направлением оси у (рис. 4, б, д) и наоборот (рис. 4, в, г).

При принятом направлении оси у вверх, знаки правой и левой частей уравнения (5) всегда одинаковы, т.е. при y» > 0 и М_и > 0, а при y» < 0 и М_и < 0. Поэтому выражение 5) представим как

d ² y/dx² = М_и / (EI_z ).

(6)

Для нахождения уравнений, определяющих деформации сечений стержня или их угловые и линейные перемещения, необходимо произвести интегрирование уравнения. Проинтегрировав уравнение один раз, получим уравнение углов поворота

θ = dy/dx = . (7)

Интегрируя уравнение (5.80) второй раз, получим уравнение прогибов

, (8)

где С и D – постоянные интегрирования, определяемые из граничных условий, каковыми являются условия крепления изгибаемых стержней.

Так, для стержня, жестко закрепленного одним концом, в месте крепления должны быть равны нулю и прогиб у, и угол поворота сечения. Для стержня, опирающегося на шарнирные крепления, прогиб равен нулю в местах крепления.

Пример .

Определить прогиб и угол поворота свободного конца консоли стержня (рис 4, а) длиной ℓ , нагруженного на конце сосредоточенной силой F. Жесткость стержня постоянна по длине и равна EI .

Начало координат примем в точке В жесткого закрепления стержня. Ось у направим вверх, ось х – вправо.

В произвольном поперечном сечении, отстоящем на расстоянии х от начала координат, изгибающий момент равен М_и = –F (ℓ – x).

Дифференциальное уравнение изогнутой оси примет вид EI(d² y/dx² ) = –F(ℓ – x).

Интегрируя это уравнение, получим EI(dy/dx) = = –F× [ℓx – (x² /2)] + С. Интегрируя далее, получим уравнение прогибов

EIy = –F [(ℓx ² /2) – (x³ /6)] + Cx + D.

Приняв во внимание, что в месте закрепления при х =0 прогиб у и угол поворота сечения θ = dy/dx равны нулю, найдем, что постоянные интегрирования С =0 и D = 0. Тогда на свободном конце стержня при х = ℓ, прогиб y = (–Fℓ³ )/(3EI) и угол поворота торцового сечения θ = dy/dx = (–Fℓ² )/(2EI).

Знак минус в выражениях прогиба и угла поворота указывает, что прогиб осуществляется в направлении, противоположном положительному направлению оси у , т.е. вниз, а торцовое сечение поворачивается по направлению движения часовой стрелки.

ЛИТЕРАТУРА

[Электронный ресурс]//URL: https://inzhpro.ru/referat/tehnicheskaya-mehanika-izgib/

1. Красковский Е.Я., Дружинин Ю.А., Филатова Е.М. Расчет и конструирование механизмов приборов и вычислительных систем: Учебное пособие. М.: – Высш. шк., 2001. – 480 с.

2. Сурин В.М. Техническая механика: Учебное пособие. – Мн.: БГУИР, 2004. – 292 с

3. Ванторин В.Д. Механизмы приборных и вычислительных систем: Учебное пособие. – М.: Высш. шк., 1999. – 415 с.