Резьбовые соединения

метки: Соединение, Резьбовой, Технический, Механик, Деталь, Напряжение, Прочность, Материал

Любая машина или механизм состоят из деталей, соединенных в сборочные единицы.

без применения сборочных операций

соединению

не соединенные на предприятии-изготовителе

Среди большого разнообразия деталей и узлов есть такие, которые используют почти во всех (или во многих) машинах: крепеж, валы, подшипники, редукторы, муфты и т.д. Такие детали (узлы) называют деталями машин общего назначения. Их изучением, расчетом и занимаются в курсе «Детали машин и основы Другие детали (узлы) встречаются только в определенных типах машин. Например, колеса, гусеницы, коленчатые валы, суппорты, крюки, штампы и т.д. Они называются деталями специального назначения и изучаются в спецкурсах.

1. Расчет деталей машин

1.1 Ряды предпочтительных чисел

это технический закон

ряды предпочтительных чисел

рядов чисел геометрической прогрессии

n	5	10	20	40	80
?	1,6	1,25	1,12	1,06	1,03
ряд	R 5	R 10	R 20	R 40	R 80

Наиболее распространенным является «средний» ряд чисел R 20:

1	1,12	1,25	1,4	1,6	1,8
2	2,24	2,5	2,8	3,15	3,55
4	4,5	5	5,6	6,3	7,1
8	9	10.

Предпочтительные числа других порядков можно получить переносом запятой в любую сторону, т.е. умножением на 10, 10 ² … 10^–2 , 10^–1 и т.д.

нормальных линейных размеров

Зная числа рядов, можно иметь «в голове» параметры многих стандартов.

1.2 Основные критерии работоспособности деталей машин

Критерий – это «мерило значения чего-либо», граница допустимости решения, ограничение целевой функции.

Важнейшими критериями работоспособности деталей машин являются прочность, жесткость, износостойкость, теплостойкость, вибрационная устойчивость.

При работоспособность деталей обеспечивают выбором материала и расчетом размеров по основному критерию. Выбор критерия обусловлен характером воздействия нагрузки, среды и вызываемым видом отказа.

В настоящее время самым распространенным критерием работоспособности является прочность.

Этому критерию должны удовлетворять все детали и узлы

принципа независимости действия сил

поверхностные напряжения

Генрих Герц

две контактные задачи

а) с первоначальным (до приложения нагрузки) контактом по линии,

например, сжатие двух цилиндров по общей образующей (рис. 1.1);

8

Вследствие упругих деформаций под действием сжимающей нагрузки w = F / l линия контакта переходит в узкую полоску шириной 2а (2а << ), на которой возникают контактные напряжения _Н , изменяющиеся по эллиптическому закону.

для первоначального контакта по линии

_Н = Z _E (w / _пр )^1/2 [_H ], (1.1)

где w = F / l – удельная (на 1 мм длины линии контакта) линейная нагрузка, Н/мм; Z _E – коэффициент влияния механических свойств материалов деталей;

1/ _пр = 1/₁ 1/₂ – приведенная кривизна поверхностей контакта: ₁ и ₂ – радиусы кривизны. Знак плюс – контакт двух выпуклых тел (рис. 1.1), знак минус – контакт выпуклого ₁ и вогнутого ₂ тел .

Рис. 1.1 Рис. 1.2

б) с первоначальным контактом в точке, например, сжатие шара на плоскости (рис. 1.2).

Числовые значения _Н намного превышают другие виды напряжений и даже пределы текучести _Т и прочности _В . Например, в подшипниках качения _{Н max} = = 4200 МПа, а _Т = 1700 МПа и _В = 1900 МПа у стали ШХ15 для них.

Кроме _Н , в зоне контакта возникают также касательные напряжения

_{Н max} = 0,3_{Н max} в точке, отстоящей от поверхности контакта на глубину 0,78а .

Отсутствие мгновенного разрушения объясняется тем, что в зоне действия _Н и _Н материал находится в условиях всестороннего объемного сжатия .

по принципу суперпозиции

По критерию [] делают оценку прочности изделия.

Виды прочностных расчетов

ориентировочный, предварительный расчет

9

основной и окончательный вид расчета

1.3 Расчет на сопротивление усталости при переменных напряжениях

1.3.1 Переменные напряжения

Нагрузка – это общее понятие силы, момента силы, давления. Нагрузки делят на статические и динамические.

не вызывает колебаний системы и приводит к постоянным напряжениям

вызывает появление колебаний и переменных напряжений

Переменные напряжения могут возникать и при постоянной нагрузке

Переменные напряжения характеризуются циклами изменения напряжений.

Характеристика цикла (рис. 1.3)

синусоидальный закон

2. Время одного цикла называют периодом Т . Если задан ресурс L , то общее число циклов N = L / T .

3. Наибольшее _max и наименьшее _min напряжения – величины алгебраические (со знаками).

Коэффициент асимметрии цикла R, Среднее напряжение, Амплитуда

Рис. 1.3

Если | _max | |_min |, то цикл называют асимметричным.

Если _min = 0, то R = 0, _m = _а = 0,5_max – цикл отнулевой (рис. 1.3, б ).

Если | _max | = |_min | и _max > 0, а _min < 0 (рис. 1.3, в ), то R = –1, _m = 0, _а = _max – цикл симметричный, самый опасный для прочности (_а = _max ).

Если R = +1, то _max = _{min .} По величине и по знаку – это постоянные напряжения.

Примечание.

и к касательным напряжениям с заменой в формулах символа на .

усталостной трещине

1.3.2 Пределы выносливости

Циклическая долговечность материалов при переменных напряжениях характеризуется кривыми усталости (кривыми Велера).

Кривые усталости (рис. 1.4) получают экспериментально на стандартных образцах, задавая им различные величины напряжений _max и фиксируя число циклов N , при которых происходит разрушение образцов.

Уравнение кривой усталости:

где С – постоянная, соответствующая условиям проведения эксперимента.

Пределом выносливости материала называют максимальное напряжение, которое может выдержать образец материала при наработке заданного числа циклов.

два характерных участка

Рис. 1.4

При N < N _lim имеет место предел ограниченной выносливости _lim (_RN ).

Как видно из рис. 1.4, чем выше напряжение , тем раньше начнется усталостное разрушение.

Связь между пределами выносливости

_lim ^q N = _{lim b} ^q N _lim , откуда _lim = _{lim b} K _L ,

где K _L = (N _lim / N )^{1/ q} называют коэффициентом долговечности.

При N N _lim принимают K _L = 1.

Показатель степени q зависит от материала, термообработки, вида напряжений, влияния условий эксперимента и т.д. Он колеблется от 4 до 20, и его значения рекомендуются в каждом конкретном случае расчета детали (узла).

на стандартных испытательных образцах

В общем случае предел выносливости детали при асимметричном цикле нагружения:

_{lim D} = 2_-1 / [(1 – R ) K _D / K _L + _D (1 + R )], (1.2)

( _{lim D} – то же с заменой символов на ),

где _-1 – предел длительной выносливости образца при симметричном цикле нагружения, МПа; R – коэффициент асимметрии цикла; K _D = (K /K _d +1/K _F – – 1) / K _V – коэффициент снижения предела выносливости при переходе от образца к реальной детали. Здесь K – эффективный коэффициент концентрации напряжений; K _d – коэффициент влияния размеров детали; K _F – коэффициент влияния качества (шероховатости) поверхности; K _V – коэффициент влияния поверхностного упрочнения (термообработки); _D – коэффициент влияния асимметрии цикла напряжений; K _L = (N _{lim D} / N _E )^{1/ q} – коэффициент долговечности детали (узла).

Здесь N _{lim D} – базовое число циклов детали ; N _Е – эквивалентное число циклов изменения напряжений:

N _E = [(_i / _max )^q N _i ], (1.3)

где _max – напряжение от длительно действующей максимальной нагрузки переменного режима; _i и N _i – постоянное напряжение и соответствующее ему число циклов i -го постоянного блока циклограммы нагружения.

Коэффициенты в формуле (1.2) выбираются по справочникам.

1.4 Коэффициенты безопасности

Коэффициенты безопасности определяют по напряжениям и :

S = _пред / _max [S ]; S = _пред / _max [S ],

при постоянных напряжениях

При совместном действии

= 2,5…4 – для хрупких материалов.

2. Резьбовые соединения

2.1 Основные виды крепежных изделий

Резьба – это образование на поверхности детали выступов и впадин, идущих по винтовой линии. Резьбовое соединение имеет две детали: с наружной резьбой (винт) и с внутренней резьбой (гайка).

Все резьбы стандартизованы .

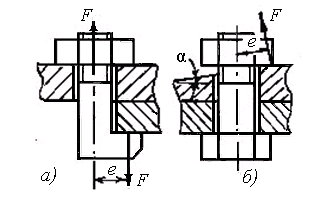
Для соединения деталей применяют болты (винт с гайкой, рис. 2.1, а ), винты (рис. 2.1, б ) – вместо гайки резьба в одной из скрепляемых деталей и шпильки (рис. 2.1, в ) – стержень с двумя нарезанными концами (синтез болта с гайкой и винта: ввинчивание по плотной посадке в деталь).

Соединения винтами – самые прогрессирующие, особенно при отсутствии в узлах мест под гайки и при высоких требованиях к их массе и внешнему виду.

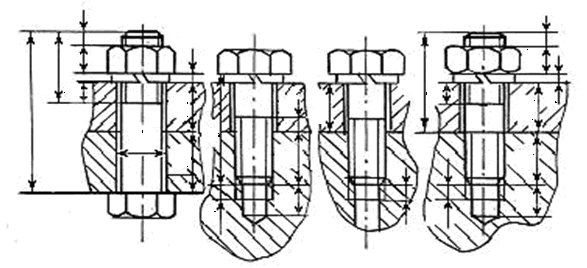
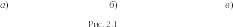
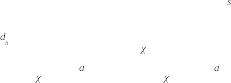
На рис. 2.1 указаны: d – номинальный (наружный) диаметр резьбы; l – длина болта, винта, шпильки; l ₀ – длина нарезанной части стержня под гайку; l ₁ – глубина завинчивания; l ₃ – выход стержня за гайку; = 6P – недорез резьбы; х = (2…2,5) Р – сбег резьбы; Н – высота гайки; Н ₁ , Н ₂ – толщины деталей; s – толщина шайбы; d _h – диаметр отверстия в деталях под стержень винта; Р – шаг резьбы.

крепежные детали разделяют на классы прочности и группы

Для стальных болтов, винтов и шпилек, Для стальных гаек

разрыв в соединении должен быть по резьбе стержня болта

Крепежные изделия в зависимости от условий эксплуатации могут быть изготовлены с защитным покрытием или без покрытия. Обозначение покрытий от 00 до 13. Например, 00 – без покрытия; 01 – цинковое с хроматированием; 02 – кадмиевое с хроматированием; 05 – окисное; 12 – серебряное; 13 – никелевое.

2.2 Краткие сведения из теории резьбовой пары

1. Момент завинчивания и осевая сила на винте

Подавляющее большинство резьбовых соединений с предварительной затяжкой. Затяжка создается при сборке с целью, чтобы после приложения рабочей нагрузки не происходило раскрытия стыка или сдвига соединяемых деталей.

При завинчивании гайки (или винта с головкой) необходимо приложить момент завинчивания Т _зав (рис. 2.2) для преодоления момента Т _Р сопротивления в резьбе и момента Т _Т сопротивления на торце гайки:

Т _зав = Т _Р + Т _Т , (2.1)

где T _P = F _t d ₂ / 2 = 0,5 F _зат d ₂ tg( + ₁ ); (2.2)

Т _Т = 0,5 F _зат f _T d _ср, (2.3)

В формулах (2.2) и (2.3): F _t – окружная (в плоскости, перпендикулярной к оси соединения) движущая сила; F _зат – осевая сила затяжки; d ₂ – средний диаметр резьбы; – угол подъема резьбы; ₁ – приведенный (с учетом влияния угла профиля ?) угол трения в резьбе: ₁ = / cos(/2), ? – угол трения материалов пары винт – гайка; f _T – коэффициент трения материалов пары гайка – деталь; d _ср – средний диаметр кольца (рис. 2.2): d _ср = 0,5 (D + d _h ).

Угол подъема резьбы определяют по среднему диаметру d ₂ (рис. 2.3):

tg = P _h / d ₂ = nP / d ₂ ,

где nP = P _h – ход резьбы, n – число заходов.

Подставляя в формулу (2.1) значения моментов Т _Р и Т _Т , получим

Т _зав = 0,5 F _зат d ₂ [tg( + ₁ ) + f _T d _ср / d ₂ ]. (2.4)

Все резьбы геометрически подобны. В среднем для метрической резьбы:

= 2 ⁰ 30; d ₂ 0,9d ; d _ср 1,4d ; ₁ = / cos30⁰ 1,15 1,15 arctgf . Тогда при f = f _T = 0,15 (резьба и торец гайки без смазки) Т _зав 0,2F _зат d . С другой стороны, принимая в среднем длину гаечного ключа L (рис. 2.2) от оси винта до середины ладони рабочего равной 14d , будем иметь момент завинчивания на ключе

Т _зав = F _P L = 14F _P d , где F _P – усилие рабочего. Из равенства 0,2F _зат d = 14F _P d получим F _зат = 70 F _P , т.е. за счет рычага на гаечном ключе и параметров соединения имеем выигрыш в силе затяжки в 70 раз. При f = f _T = 0,1 F _зат 100 F _P .

2. Самоторможение в резьбе

Самоторможение – это сохранение затянутого положения гайки так, что для ее отвинчивания следует приложить момент, противоположного направления моменту завинчивания. Момент отвинчивания:

Т _отв = 0,5 F _зат d ₂ [tg(₁ – ) + f _T d _ср / d ₂ ].

Условие самоторможения: Т _отв 0. Без учета трения на торце гайки (Т _Т = 0) должно быть tg(₁ – ) 0 и ₁ .

Если в среднем = 2 ⁰ 30, то ₁ 2⁰ 30; arctgf = ₁ / 1,15; f tg2⁰ 17 или

f 0,04. С учетом влияния момента Т _Т f 0,02.

при статической нагрузке все крепежные резьбы самотормозящие

3. КПД резьбовой пары

КПД резьбы определяют как отношение полезной работы на винте к затраченной работе на ключе при повороте гайки на произвольный угол.

Без учета трения на торце гайки КПД равен:

= tg / [tg( + ₁ )].

При = 2⁰ 30 и f = 0,1 0,3, а с учетом трения на торце (момента Т_Т ) КПД еще ниже.

4. Распределение осевой силы по виткам резьбы

На рис. 2.4 показано распределение осевой силы F _зат по виткам резьбы. На первый виток резьбы приходится около 1/3 F _зат , а на последний, десятый

виток – менее 1/100 F _зат . Основная причина столь неравномерной нагрузки – разноименное сочетание деформаций витков: болт растянут, гайка сжата .

Не имеет смысла увеличивать высоту гайки за счет числа z витков (более десяти).

Например, у стандартных шестигранных гаек при Н = 0,8d z = 6.

на создание одноименных деформаций в районе первых витков

5. Прочность резьбового участка стержня болта

При сборке стержень болта растягивается силой F _зат и скручивается моментом Т _Р сил сопротивления в резьбе. Момент Т _Т на торце гайки на стержень не передается.

Эквивалентное напряжение для пластичных материалов:

_Е = (² + 3² )^1/2 []_Р , (2.5)

где = F _зат /А ; А = d _P ² / 4; = T _P / W _К ; T _P = 0,5d ₂ tg( + ₁ ); W _К = d _P ³ / 16.

За расчетный диаметр d _Р принят d ₁ – внутренний диаметр резьбы стержня.

Формулу (2.5) после подстановки в нее и представим в виде

_Е = {1 + 12 [tg( + ₁ ) d ₂ /d ₁ ]² }^1/2 []_Р .

При = 2,5 ⁰ ; ₁ = 1,15arctgf и f = 0,15 ₁ = 9,8⁰ ; d ₂ / d ₁ 1,06 будем иметь _Е = 1,28. За расчетное значение принимают 1,3.

Условие прочности при затяжке гайки:

= 1,3 F _зат / (d ₁ ² / 4) []_Р , (2.6)

коэффициент

Рассчитывая напряжения по формуле (2.6), следует сделать вывод: при затяжке гаек с резьбой меньше М12 обязательно должен быть контроль усилия затяжки во избежание разрушения болтов .

6. Прочность витков резьбы на срез

Из условия равнопрочности витков

7. Эксцентричное нагружение болта

Эксцентричная нагрузка возникает

а) в болтах с так называемой костыльной головкой (рис. 2.6, а );

б) при перекосах опорных поверхностей под гайкой или головкой болта

(рис. 2.6, б ).

Рис. 2.6

Рис. 2.7

Под действием силы F в стержне болта действуют напряжения растяжения _Р и изгиба _и . При этом, как показывают расчеты, _и во много раз может превышать _Р . Напряжения изгиба являются самыми опасными для прочности болтов, винтов и шпилек .

Отсюда правила конструирования:

1. Не допускать черновых (необработанных) поверхностей под гайками, головками, шайбами.

2. Несопрягаемые (свободные) поверхности корпусных деталей не обрабатывают. В местах установки крепежа следует предусматривать:

а) на литых деталях – бобышки (местные выступы) под обработку высотой S = 2…3 мм (рис. 2.7, а );

• б) на сварных деталях – платики (рис. 2.7, б );

в) на любых деталях – цековки глубиной h = 1,25…1,6 мм (рис. 2.7, в ).

3) Использовать сферические, косые шайбы и другие выравнивающие от изгиба устройства.

2.3 Расчет болтовых соединений

Как правило, детали соединяются несколькими болтами, т.е. группой болтов. При расчете приняты следующие допущения:

1. все болты одинаковые и равнозатянутые;

2) поверхности стыка деталей не деформируются, остаются плоскими;

3) как правило, стыки имеют оси симметрии, болты располагаются симметрично относительно этих осей.

Расчет группового болтового соединения сводится к отысканию нагрузки для наиболее нагруженного болта и его расчету на прочность как единичного.

Выразив силы F _{T 2,} F _{T 3} … F _{Ti _} через F _{T 1} – наибольшую по величине, находящуюся на наибольшем расстоянии ₁ – F _{T 2} = F _{T 12} /₁ , …, F _Ti = F _{T 1 i} / ₁ , – и, подставив их в условие (2.9), получим

Т = F _{T 11} ² /₁ + F _{T 12} ² /₁ + … + F _{T 1 i} ² /₁ .

Отсюда F _{T 1} = Т ₁ / (₁ ² + ₂ ² + …+ _i ² ).

В общем виде для i -го болта

F _{Т i} = 10³ Т _i / (_i ² ), (2.10)

где Т , Нм; _i , мм; i = 1, 2…z .

3. При совместном действии силы F _F и силы F _{Т i} определяют полную сдвигающую силу F _d , действующую на наиболее нагруженный болт. На рис. 2.9 это болт 1 – угол между векторами F _F и F _{Т 1} острый. Для него по теореме косинусов сдвигающая сила будет равна:

F _{d 1} = [F _{Т 1} ² + F _F ² – 2F _{Т 1} F _F cos(F _{Т 1} F _F )]^1/2 .

отсутствие сдвига деталей в стыке

Соединение может быть выполнено в двух вариантах:

• а) на болтах, установленных в отверстия деталей с зазором;
• б) на болтах (по ГОСТ 7817–80), установленных в отверстия плотно, без зазора.

5. Болт с зазором. Сила F _d уравновешивается силами трения F _f на стыках. Они создаются силой затяжки F _зат болта при сборке (рис. 2.10): F _f = iF _зат f F _d . Откуда требуемая сила затяжки

F _зат = KF _d / (if ), (2.11)

где К = 1,5…2 – коэффициент запаса затяжки на сдвиг; i – число плоскостей стыка; f – коэффициент трения материалов деталей на стыке.

Если, например, принять К = 1,5, f = 0,15, i = 1, то требуемая сила F _зат должна быть в 10 раз больше внешней сдвигающей силы F _d . Отсюда большие

1. Нагрузка в зоне болта от центральной силы F _z : F _F = F _z / z .

2. Сила F _М от изгибающих моментов М распределяется по болтам (рис. 2.12) пропорционально их расстояниям от центральных осей.

F = F _F + F _{М x max} + F _{М y max} ,(2.13)

где знак плюс, если F _z растягивает стык; знак минус, если F _z сжимает стык.

Рис. 2.13

4. Возможность раскрытия стыка силой F предварительной затяжкой болтов F _зат. Применяют болты с зазором. При сборке соединения силой F _зат (рис. 2.13, а ) стержень болта растягивается, а соединяемые детали сжимаются (условно считают в пределах конусов 1 , 2 и цилиндра 3 сжатия).

После приложения к деталям внешней силы F (рис. 2.13, б )болт дополнительно растянется на величину l _Б , а детали ослабят свое первоначальное сжатие на l _Д (разгрузка стыка).

Условие равновесия сил

Q _Б + Q _Д = F , (2.14)

где Q _Б – часть внешней нагрузки, приходящейся на болт, Q _Д – часть внешней нагрузки, идущей на ослабление сжатого силой F _зат стыка.

Условие совместности деформаций

l _Б = l _Д , (2.15)

где по закону Гука l = Ql / (EA ) = Q , здесь Е – модуль упругости материала; А – площадь поперечного сечения на длине l ; = l / (EA ) – податливость, мм/Н.

Тогда из условия (2.14) Q _Д = F – Q _Б и из условия (2.15) будем иметь Q _ББ = (F – Q _Б )_Д . Откуда Q _Б = F _Д / (_Б + _Д ).

Соотношение податливостей называют коэффициентом основной (внешней) нагрузки: = _Д / (_Б + _Д ).

Тогда Q _Б = F и Q _Д = (1 – ) F . Только часть внешней силы F идет на дополнительное растяжение болта , остальная часть (1 – ) F расходуется на разгрузку сжатого стыка деталей (уменьшение силы затяжки в них).

Для жесткого стыка (стальные, чугунные детали) определено, что =

= 0,2… 0,3. При наличии в стыке упругих прокладок (медь, алюминий, картон, резина и т.д.) растет к единице. Если Q _Д = F _зат или F = F _зат / (1 –

чем больше сила затяжки F

Расчетная сила на болт с учетом скручивания стержня при затяжке гайки:

F _Б = 1,3F _зат + F . (2.16)

2.4 Сила затяжки

1. Сила затяжки из условия отсутствия сдвига

В случае общей схемы нагружения (рис. 2.8), кроме сдвигающей силы F _d , на стык действуют еще отрывающие F _z , M _x , M _y . Влияние моментов M _x и M _y не учитывают, поскольку (рис. 2.14) они не изменяют суммарной силы трения F _f на стыке (компенсация: слева – F _f , справа + F _f ).

Отрывающая сила F _z ослабляет давление и силу трения на стыке и требует увеличения затяжки. Сжимающая сила F _z увеличивает силу трения. На ослабление или усиление стыка деталей расходуется часть внешней нагрузки (1 – )F _z .

2. Сила затяжки из условия нераскрытия стыка

В этом случае каждый из z болтов предварительно затянут силой F _зат2 , т.е. весь стык нагружен силой zF _{зат 2} . Напряжения сжатия на стыке при этом:

_зат = zF _зат2 / A _ст ,

где А _ст – площадь стыка, мм² , (рис. 2.15).

Отрывающая сила F _z разгружает стык на величину (1 – )F _z . Напряжения сжатия _зат на стыке уменьшатся на _F = (1 – ) F _z / A _ст .

Наибольшие напряжения от изгиба стыка моментом М действуют в точках А и В . С учетом податливостей элементов соединения _М = 10³ (1 – ) М /W _ст ,

2.5 Порядок расчета болтов для общей схемы нагружения

2.5.1 Расчет при статической нагрузке

1. Расчетная осевая сила на наиболее нагруженном болте (болт с зазором) по формуле (2.16)

F _Б = 1,3F _зат + F ,

где F _зат определяют по формулам (2.17) и (2.18).

Если F _зат1 > F _зат2 (например, в 1,5 и более раза), то для восприятия силы F _d следует применятьразгружающие стык от сдвига а в формулу (2.16) подставлять значение F_зат2 .

2. Возможность затяжки болтов рабочим стандартным гаечным ключом определяется из соотношения F _зат = 70F _раб , откуда требуемое усилие рабочего: F _раб = F _зат / 70 [F _раб ] = [200…300] Н.

Если F _раб < [F _раб ], то необходим контроль затяжки при сборке.

Если F _раб > [F _раб ], то следует предусмотреть дополнительные меры по обеспечению F _зат.

3. В проектировочном расчете находят внутренний диаметр резьбы болта d ₁ , мм:

d ₁ = [4F _Б / ([]_P )]^1/2 , (2.19)

где [] _P = _Т / [S ], МПа (_Т определяют по выбранному классу прочности ; [S ] – коэффициент безопасности).

Расчетный диаметр d ₁ округляется в большую сторону до d ₁ по ГОСТ 24705–81.

4. определяется длина болта l , мм:

l = _i + l ₃ ,

где _i – сумма толщин всех соединяемых деталей, мм; l ₃ – запас на выход стержня болта за пределы гайки, мм.

Длина l округляется по ГОСТ на болты .

5. Если размеры болтов известны (например по рекомендациям), то из формулы (2.19) определяют _Р и требуемую величину _Т :

_Р = 4F _Б / (d ₁ ² ); _Т = _Р [S ].

По величине _Т назначают безопасный класс прочности болта из условия _{Т Т} , где _Т – предел текучести материала, соответствующий выбранному классу прочности.

2.5.2 Расчет при переменной нагрузке

Проводят проверочный расчет по коэффициентам безопасности:

на предотвращение пластической деформации

S _Т = _Т / _max = _Т / (_зат + 2_а ) [S _Т ] = 1,25…2,5,

где _зат = 1,3F _зат / А ₁ – напряжение предварительной затяжки, МПа; А ₁ – расчетная площадь сечения болта по d ₁ , мм² ; _а = (F _{Б max} – F _{Б min} ) / (2A ₁ ) – амплитуда напряжений, МПа; F _{Б max} и F _{Б min} – соответственно максимальная и минимальная внешняя нагрузка на оси болта по формуле (2.16), Н;

на ограничение амплитуды цикла

S _a = _{a lim} / _a [S _a ] = 2,5…4,

где _{a lim} = _{— l Р} K _d K _V / K – предельная амплитуда цикла, МПа; _{— l Р} – предел выносливости гладкого образца при симметричном цикле напряжений растяжение-сжатие; K _d – коэффициент влияния размеров болта; K _V – коэффициент влияния качества поверхностного слоя; K – эффективный коэффициент концентрации напряжений.

Все параметры, входящие в формулу _{a lim} выбирают по справочникам.

3. Механические передачи

3.1 Общие сведения

делятся на две группы

• передачи зацеплением (зубчатые: цилиндрические, конические;
• червячные;
• цепные;
• зубчато-ременные;
• винт-гайка);

• передачи трением (фрикционные и ременные).

К разновидностям цилиндрических передач относятся планетарные, волновые, реечные и винтовые, а конических – гипоидные.

Конкретный состав передач в приводе зависит

1) общего передаточного числа привода и ₀ ;

2) компоновки привода, т.е. от объема заданного проcтранства, в котором должен размещаться привод, и взаимного расположения в нем осей валов;

3) технико-экономических возможностей конкретного предприятия.

зубчатые цилиндрические передачи

3.2 Характеристика передач привода

Основные характеристики:

1. нагрузка на рабочем органе: сила, вращающий момент или мощность и характер (циклограмма) ее изменения;

2. скорость рабочего органа;

3. ресурс – в частности, срок службы.

Эти характеристики минимально необходимы и достаточны для проектировочного расчета любой передачи.

Кроме основных, важное значение имеют дополнительные характеристики:

1. общее передаточное число привода и ₀ = и ₁ и ₂ …и _i , где и _i – передаточное число одной i -й ступени передач.

2. общий КПД привода : ?₀ = ?₁ ?₂ …?_i , где ?_i – КПД одной i -й кинематической пары;

3. потребная (расчетная) мощность двигателя Р _дв ? :

Р _дв ? = T _р.о n _р.о / 9550?₀ ,

где T _р.о , n _р.о – соответственно вращающий момент и частота вращения рабочего органа;

1. частота вращения i-го вала (i = 1,2,3…k ; i = 1 – вал двигателя; i = k – вал рабочего органа): n _{i =} n ₁ / и _{1 — i} , где и _{1 — i} – передаточное число между первым и i- м валами;

вращающий момент i-го вала:

T _i = Т _{р . о} / (и _k-i ?_k-i ),

где и _{k — i} ,?_{k — i} – соответственно передаточное число и КПД между k -м (рабочего органа) и i- м валами.