«Математика – царица наук, физика ее правая рука, химия – левая».
Предмет исследования – производная.
Ведущая цель — показать значимость производной не только в математике, но и в других науках, её важность в современной жизни.
Дифференциальное исчисление – это описание окружающего нас мира, выполненное на математическом языке. Производная помогает нам успешно решать не только математические задачи, но и задачи практического характера в разных областях науки и техники.
Производная функции используется всюду, где есть неравномерное протекание процесса: это и неравномерное механическое движение, и переменный ток, и химические реакции и радиоактивный распад вещества и т.д.
Ключевой и тематический вопросы данного реферата:
1. История возникновения производной.
2. Зачем изучать производные функций?
3. Где используются производные?
4. Применение производных в физике, химии, биологии и других науках.
5. Выводы
Я решила написать работу на тему «Применение производной в различных областях науки», потому что считаю эту тему очень интересной, полезной и актуальной.
В своей работе я расскажу о применении дифференцирования в различных областях науки, таких как химия, физика, биология, география и т. д. Ведь все науки неразрывно связаны между собой, что очень хорошо видно на примере рассматриваемой мною темы.
Применение производной в различных областях науки, Из курса алгебры старших классов мы уже знаем, что
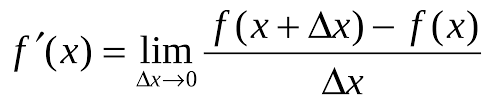
Действие нахождения производной называется её дифференцированием, а функцию, имеющую производную в точке х, называют дифференцируемой в этой точке. Функция, дифференцируемая в каждой точке промежутка, называется дифференцируемой в этом промежутке.
Честь открытия основных законов математического анализа принадлежит английскому физику и математику Исааку Ньютону и немецкому математику, физику, философу Лейбницу.
Канифольно-экстрактивное производство. Характеристика и области ...
... также в производстве граммофонных пластинок и в строительном деле как добавка к бетонам, чтобы придать им текучесть при заливке форм и гидроустойчивость. Канифольно-терпентинная промышленность осваивает ... отраслях народного хозяйства. Области применения их непрерывно расширяются. Как канифоль, так и скипидар используются в натуральном виде, а также и в виде многочисленных производных и служат ...
Ньютон ввел понятие производной, изучая законы механики, тем самым раскрыл её механический смысл., Физический смысл производной: производная функции

Лейбниц пришёл к понятию производной, решая задачу проведения касательной к производной линии, объяснив этим ее геометрический смысл.
Геометрический смысл производной состоит в том, что производная функция в точке

Термин производная и современные обозначения
Российский математик 19 века Панфутий Львович Чебышев говорил, что «особенную важность имеют те методы науки, которые позволяют решать задачу, общую для всей практической деятельности человека, например, как располагать своими средствами для достижения наибольшей выгоды».
С такими задачами в наше время приходится иметь дело представителям самых разных специальностей:
-
Инженеры технологи стараются так организовать производство, чтобы выпускалось как можно больше продукции;
-
Конструкторы пытаются разработать прибор для космического корабля так, чтобы масса прибора была наименьшей;
-
Экономисты стараются спланировать связи завода с источниками сырья так, чтобы транспортные расходы оказались минимальными.
При изучении любой темы у учеников возникает вопрос: «Зачем нам это надо?» Если ответ удовлетворит любопытство, то можно говорить о заинтересованности учеников. Ответ для темы «Производная» можно получить, зная, где используются производные функций.
Чтобы ответить на этот вопрос, можно перечислить некоторые дисциплины и их разделы, в которых применяются производные.
Производная в алгебре:
1. Касательная к графику функции 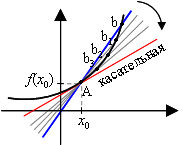
Касательная к графику функции f, дифференцируемой в точке x о , — это прямая, проходящая через точку (x о ; f (x о )) и имеющая угловой коэффициент f ′(x о ).
y = f (x о ) + f ′(x о ) (x – x о )
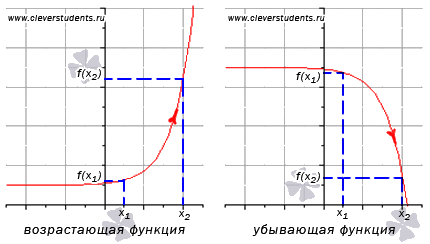
2. Поиск промежутков возрастания и убывания функции
Функция y=f(x) возрастает на интервале X , если для любых ![]() и
и ![]() выполняется неравенство
выполняется неравенство ![]() . Другими словами – большему значению аргумента соответствует большее значение функции.
. Другими словами – большему значению аргумента соответствует большее значение функции.
Применение производной в науке и техникe
Во второй главе моего реферата речь пойдёт о применении производной в науке и технике и о решении задач в этой области. 1. Теоретическая часть 1.1 Задачи, приводящие к понятию производной При изучении тех или ...
Функция y=f(x) убывает на интервале X , если для любых ![]() и
и ![]() выполняется неравенство
выполняется неравенство ![]() . Другими словами – большему значению аргумента соответствует меньшее значение функции.
. Другими словами – большему значению аргумента соответствует меньшее значение функции.
3. Поиск точек экстремума функции
точкой максимума
точкой минимума
Под окрестностью точки
Точки минимума и максимума называют точками экстремума , а значения функции, соответствующие точкам экстремума, называют экстремумами функции .
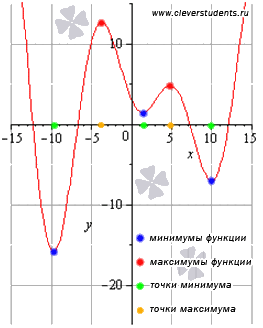 поиск точек экстремума функции 1">
поиск точек экстремума функции 1">
4. Поиск промежутков выпуклости и вогнутости функции
График функции ![]() , дифференцируемой на интервале
, дифференцируемой на интервале ![]() , является на этом интервале выпуклым , если график этой функции в пределах интервала
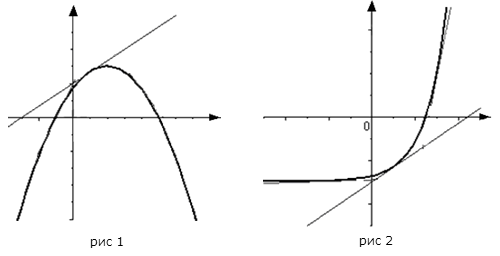
, является на этом интервале выпуклым , если график этой функции в пределах интервала ![]() лежит не выше любой своей касательной (рис. 1).
лежит не выше любой своей касательной (рис. 1).
Интегрирующие цифровые вольтметры с усреднением мгновенных результатов ...
... погрешность , , подавление помех на 70 дБ. Цифровые вольтметры переменного тока Как мы уже отмечали ранее, ЦВ встречаются в пределах ... в трех вариантах: усреднение групп мгновенных значений, разделенных интервалом времени, кратным нечетному числу полупериодов U п ; ... путем подачи сигнала на схему совпадения (СС), выполняющую функции селектора. На второй вход СС подаются импульсы длительностью , ...
График функции ![]() , дифференцируемой на интервале
, дифференцируемой на интервале ![]() , является на этом интервале вогнутым , если график этой функции в пределах интервала
, является на этом интервале вогнутым , если график этой функции в пределах интервала ![]() лежит не ниже любой своей касательной (рис. 2).
лежит не ниже любой своей касательной (рис. 2).
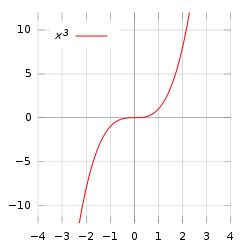
Точкой перегиба графика функции ![]() называется точка
называется точка ![]() , разделяющая промежутки выпуклости и вогнутости.
, разделяющая промежутки выпуклости и вогнутости.
5. Поиск точек изгиба функции
Производная в физике:
1. Скорость как производная пути 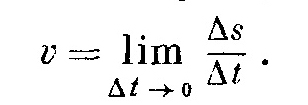
2. Ускорение как производная скорости ![]() a =
a = ![]()
3. Скорость распада радиоактивных элементов ![]() = — λN
= — λN
А так же в физике производную применяют для вычисления:
Скорости материальной точки ![]()
Мгновенной скорости как физический смысл производной, Мгновенное значение силы переменного тока
Мгновенное значение ЭДС электромагнитной индукции 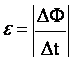
Производная, ее применение в физике и техники
... механики, физики и других отраслей знания возникла необходимость с помощью одного и того же аналитического процесса из данной функции y=f(x) получать новую функцию, которую называют производной функцией (или просто производной) данной функции f(x) и ...
Максимальную мощность ![]()
Производная в химии:
И в химии нашло широкое применение дифференциальное исчисление для построения математических моделей химических реакций и последующего описания их свойств.
V (t) = p ‘(t)
Количество
в-ва в момент времени
p = p(t 0 )
Функция
Интервал времени
∆ t = t– t 0
Приращение аргумента, Изменение количества в-ва
∆ p= p(t 0 + ∆ t ) – p(t 0 )
Приращение функции, Средняя скорость химической реакции
∆ p/∆t
Отношение приращёния функции к приращёнию аргумента, Производная в биологии:
Популяция – это совокупность особей данного вида, занимающих определённый участок территории внутри ареала вида, свободно скрещивающихся между собой и частично или полностью изолированных от других популяций, а также является элементарной единицей эволюции.
Р = х‘ (t)
Производная в географии:, Производная помогает рассчитать:
1. Некоторые значения в сейсмографии
2. Особенности электромагнитного поля земли
3. Радиоактивность ядерно- геоифзичексих показателей
4.Многие значения в экономической географии
5.Вывести формулу для вычисления численности населения на территории в момент времени t.
у’= к у
Идея социологической модели Томаса Мальтуса состоит в том, что прирост населения пропорционально числу населения в данный момент времени t через N(t) .Модель Мальтуса неплохо действовала для описания численности населения США с 1790 по 1860 годы. Ныне эта модель в большинстве стран не действует
Производная в электротехнике:
В наших домах, на транспорте, на заводах : всюду работает электрический ток. Под электрическим током понимают направленное движение свободных электрически заряженных частиц.
Количественной характеристикой электрического тока является сила тока.
В цепи электрического тока электрический заряд меняется с течением времени по закону q=q (t).
Сила тока I есть производная заряда q по времени.
В электротехнике в основном используется работа переменного тока.
Электрический ток, изменяющийся со временем, называют переменным. Цепь переменного тока может содержать различные элементы: нагревательные приборы, катушки, конденсаторы.
Получение переменного электрического тока основано на законе электромагнитной индукции, формулировка которого содержит производную магнитного потока.
По алгебре «Понятие функции»
... функции. Данный реферат содержит много материала, связанного с понятием функции в школьном курсе, дает возможность понять, что функция играет важную роль в практической деятельности человека. 2. Из истории математики., ...
Производная в экономике:
Экономика – основа жизни, а в ней важное место занимает дифференциальное исчисление – аппарат для экономического анализа. Базовая задача экономического анализа – изучение связей экономических величин в виде функций.
Производная в экономике решает важные вопросы:
1. В каком направлении изменится доход государства при увеличении налогов или при введении таможенных пошлин?
2. Увеличится или уменьшится выручка фирмы при увеличение цены на её продукцию?
Для решения этих вопросов нужно построить функции связи входящих переменных, которые затем изучаются методами дифференциального исчисления.
Также с помощью экстремума функции (производной) в экономике можно найти наивысшую производительность труда, максимальную прибыль, максимальный выпуск и минимальные издержки.
ВЫВОД: производная успешно применяется при решении различных прикладных задач в науке, технике и жизни
Как видно из вышеперечисленного применение производной функции весьма многообразно и не только при изучении математики, но и других дисциплин. Поэтому можно сделать вывод, что изучение темы: «Производная функции» будет иметь своё применение в других темах и предметах.
Мы убедились в важности изучения темы «Производная», ее роли в исследовании процессов науки и техники, в возможности конструирования по реальным событиям математические модели, и решать важные задачи.
В заключении я хочу вам прочитать стихотворение:, Музыка может возвышать или умиротворять душу,
Живопись – радовать глаз,
Поэзия – пробуждать чувства,
Философия – удовлетворять потребности разума,
Инженерное дело – совершенствовать материальную сторону жизни людей,
математика способна достичь всех этих целей”.
Морис Клайн.
Список используемой литературы:
[Электронный ресурс]//URL: https://inzhpro.ru/referat/proizvodnaya-v-stroitelstve/
1. Богомолов Н.В., Самойленко И.И. Математика. — М.: Юрайт, 2015.
2. Григорьев В.П., Дубинский Ю.А, Элементы высшей математики. — М.: Академия, 2014.
3. Баврин И.И. Основы высшей математики. — М.: Высшая школа, 2013.
4. Богомолов Н.В. Практические занятия по математике. — М.: Высшая школа, 2013.
5. Богомолов Н.В. Сборник задач по математике. — М.: Дрофа, 2013.
6. Рыбников К.А. История математики, «Издательство Московского университета», М, 1960.
7. Виноградов Ю.Н., Гомола А.И., Потапов В.И., Соколова Е.В. – М.:
8 . Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия. – М.: Издательский центр «Академия», 2016
Периодические источники:, Газеты и журналы: «Математика», «Открытый урок», Использование ресурсов сети Интернет, электронных библиотек:
www:egetutor.ru
matematika-na5.norod.ru
