Сложные деформации. Местные напряжения

метки: Представление, Состояние, Конструкция, Напряженный, Напряжение, Прочность, Материал, Сечение

БЕЛОРУССКИЙ ГОСУДРАСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ

Кафедра инженерной графики

РЕФЕРАТ

На тему:

«Сложные деформации. Местные напряжения»

МИНСК, 2008

Сложные деформации

Мы рассмотрели четыре вида простого нагружения стержней, четыре простейшие типа их деформаций: растяжение (сжатие), сдвиг, кручение и плоский изгиб. На практике многие детали одновременно подвергаются нескольким простым деформациям, например, кручению и изгибу, изгибу и сжатию и т.д. Рассмотрим расчет на прочность при таком нагружении.

Понятие о теориях прочности

опасного или предельного состояния материала

Теории прочности

Физические процессы, происходящие при переходе в опасные состояния, сильно различаются для пластичных и хрупких материалов, поэтому существенно могут различаться и условия перехода в эти состояния.

Первая теория прочности, или теория наибольших нормальных напряжений, Вторая теория прочности, или теория наибольших деформаций, Третья теория прочности, или теория наибольших касательных напряжений

, (1)

где σ _red – приведенное или эквивалентное нормальное напряжение; σ , τ – соответственно нормальное и касательное действующие напряжения; σ _adm – допускаемое напряжение материала при растяжении. Третья теория прочности широко применяется для пластичных материалов, одинаково сопротивляющихся растяжению и сжатию.

Энергетическая (четвертая) теория прочности

. (2)

Изгиб с кручением стержней круглого поперечного сечения

При сложных деформациях в поперечных сечениях стержней действуют одновременно несколько составляющих внутренних сил, например, крутящий и изгибающий моменты, поперечная и продольная силы. Расчеты на прочность в этом случае основаны на принципе независимости действия сил с применением выбранной теории прочности. Выбор гипотезы прочности определяется прежде всего состоянием материала – пластическим или хрупким.

Решают такие задачи в следующем порядке. Сначала в поперечных сечениях стержня определяют с помощью метода сечений внутренние силы. Для определения положения опасного сечения необходимо построить эпюры внутренних сил. Далее определяют нормальные и касательные напряжения от каждой составляющей внутренних сил. Анализируя распределение напряжений по длине стержня, определяют наиболее нагруженное сечение и наиболее нагруженную точку. Для нее составляют условие прочности с привлечением используемой гипотезы прочности.

Длительная прочность металлов

... доведении стержня постоянного сечения до разрушения под действием постоянной растягивающей нагрузки при постоянной температуре [1]. В результате испытаний устанавливается предел длительной прочности, т.е. напряжение, вызывающее разрушение металла за ...

Деформации изгиба с кручением подвергаются валы различных передаточных механизмов. Расчет валов на прочность при действии указанных деформаций называют расчетом на статическую прочность по наибольшим усилиям.

На рис. 1, а показана схема нагружения, действующая на двухопорный вал. Для удобства расчета пространственную систему внешних сил представляют в виде сил, вызывающих одновременно изгиб в вертикальной (F _{1 y} , F_{2 y} ) и горизонтальной (F_{1 z} , F_{2 z} ) плоскостях. Вал принимается за статически определимый стержень (рис. 1, б).

Соответственно реакции опор определяют в виде составляющих, действующих в вертикальной (R_AY , R_BY ) и горизонтальной (R_AZ , R_BZ ) плоскостях.

На участке вала CD в поперечных сечениях действует крутящий момент Т , равный внешним скручивающим моментам Т_е . Под действием приложенной нагрузки в сечениях возникают нормальные от изгиба и касательные от изгиба и кручения напряжения. Величиной касательных напряжений от изгиба пренебрегают, так как она незначительна по сравнению с величиной касательных напряжений от кручения.

в

Рис. 1

д

г

а

б

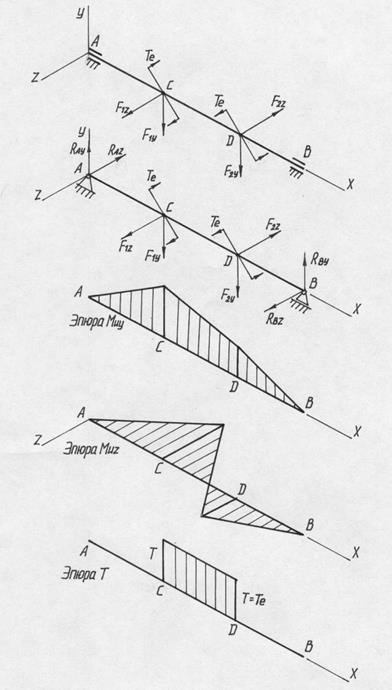
Используя принцип независимости действия сил, строим эпюры изгибающих моментов от вертикальных (рис. 1, в) и горизонтальных сил (рис. 1, г), а также эпюру крутящих моментов (рис. 1, д).

Сравнивая построенные эпюры, видим, что наиболее опасным является сечение, проходящее через точку С . В этом поперечном сечении помимо крутящего действует и изгибающий момент, величина которого определяется как

. (3)

Известно, что максимальные нормальные напряжения при изгибе будут в крайних волокнах и равны , где W ≈ 0,1d³ – осевой момент сопротивления сечения в виде круга диаметром d . Наибольшие касательные напряжения при кручении возникают в наиболее удаленных от центра точках сечения и определяются как τ = T/W_p = T/(2W), где W_p – полярный момент сопротивления сечения, для круга W_p ≈ 0,2d³ . Подставляя значения σ и τ в выражения (1) и (2), запишем соответственно условия прочности вала при использовании третьей и четвертой гипотез прочности:

(4)

и , (5)

где σ _adm – допускаемое напряжение материала вала при растяжении. Из выражений (4) и (5) можно найти значение осевого момента сопротивления W поперечного сечения вала как или и далее величину диаметра вала .

Местные напряжения

местными напряжениями

Концентрация напряжений

концентрацией

Так, при растяжении полосы (рис. 2, а, б, в) силами F в сечениях k – k напряжения равны номинальным σ = F/A, где А – площадь поперечного сечения полосы. При наличии в пластине отверстия (рис. 2, б) или выточки (рис. 2, в) распределение напряжений изменяется: у краев отверстия и выточки напряжения максимальны (σ_max ) и много больше расчетных. Подобное можно наблюдать при изгибе (рис. 3, а), где σ = М_и /W = (F·ℓ)/W, а σ_max > σ.

в

б

а

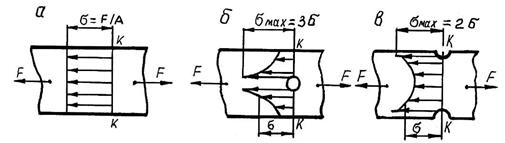
Рис. 2

теоретический

Теоретический коэффициент концентрации α

эффективного коэффициента концентрации К _σ

обязательно должна учитываться

галтелями

б

а

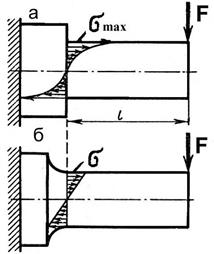
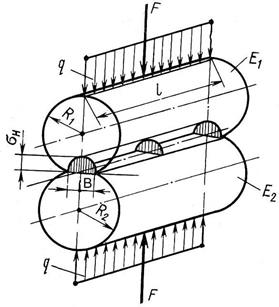
Рис. 3 Рис. 4

Контактные напряжения

Большие местные напряжения возникают в местах соприкосновения действующих друг на друга тел. Напряжения, возникающие в месте соприкосновения двух прижатых друг к другу тел, называют контактными. В месте соприкосновения тел вследствие деформации материала образуется площадка контакта.

По контактным напряжениям рассчитывают фрикционные и зубчатые передачи, элементы кулачковых механизмов. Определение контактных напряжений при малых размерах площадок контакта для тел различной конфигурации (контактная задача) рассматривается в теории упругости. Расчет базируется на следующих допущениях: в месте контакта возникают только упругие деформации; поверхности соприкасающихся тел идеально гладкие, и силы давления, распределенные по площадке контакта, нормальны к поверхности контакта; на площадке контакта возникают только нормальные напряжения. При размерах площадок контакта, малых по сравнению с общей поверхностью соприкасающихся тел, для определения контактных напряжений используют зависимости, полученные Г. Герцем. Напряжения в месте контакта зависят от геометрии соприкасающихся тел. Приведем без вывода расчетные формулы для случая сжатия двух цилиндров (рис. 4) с радиусами R ₁ и R ₂ и длиной ℓ по образующей. Считают, что сила прижатия F передается через узкую площадку контакта шириной b и длиной ℓ . Возникающие на площадке нормальные напряжения распределяются по ее ширине в эллиптической зависимости, достигая наибольшего значения в точках оси площадки. Величина наибольших контактных напряжений, как показал Герц, равна

, (6)

где q = F/ℓ – удельная нагрузка; E _п = 2E₁ E₂ /(E₁ + E₂ ) – приведенный модуль упругости материалов цилиндров; μ – коэффициент Пуассона материала; ρ_п = R₁ R₂ /(R₁ ± R₂ ) – приведенный радиус кривизны цилиндров, знак «–» берут в случае контакта выпуклой поверхности радиусом R ₂ с вогнутой поверхностью радиусом R ₁ . Для материалов с коэффициентом Пуассона μ = 0,3 выражение (6) примет вид

. (7)

Из формулы (7) следует, что контактные напряжения не являются линейной функцией сжимающей силы F и зависят от модуля упругости материала. Они меняются медленнее, чем сама сила, что связано с изменением ширины площадки контакта.

Если размеры площадки контакта соприкасающихся тел значительны и сопоставимы с величиной радиуса кривизны соприкасаемых поверхностей, имеет место деформация смятия . Например, деформацию смятия рассматривают при определении контактных напряжений между боковой поверхностью заклепки, болта и цилиндрической поверхностью отверстия. Считают, что напряжения смятия распределены по площадке контакта равномерно, перпендикулярны к ней и определяются как

σ _con = F/A_con , (8)

где F – сила прижатия контактирующих тел; А_соп – площадь смятия. В качестве площади смятия принимают не фактическую, а некоторую условную площадку контакта. Так, если поверхность смятия цилиндрическая (например, поверхность соприкосновения заклепки и листа), то в расчетную формулу (8) подставляют площадь, равную проекции поверхности соприкосновения на диаметральную плоскость. Поэтому, А_соп = k(d·h), где k – число заклепок; d·h – площадь смятия одной заклепки диаметром d ; h – высота листа, сминающего заклепку. Если поверхность смятия плоская (смятие призматических шпонок), площадь смятия определяют умножением длины на ширину. Отметим, что допускаемые напряжения на смятие принимают в 2 … 2,5 раза больше допускаемых напряжений на сжатие.

ЛИТЕРАТУРА

[Электронный ресурс]//URL: https://inzhpro.ru/referat/predstavlenie-o-napryajennom-sostoyanii-konstruktsiy/

1	Красковский Е.Я., Дружинин Ю.А., Филатова Е.М. Расчет и конструирование механизмов приборов и вычислительных систем: Учебное пособие. М.: – Высш. шк., 2001. – 480 с.	2001
2	Сурин В.М. Техническая механика: Учебное пособие. – Мн.: БГУИР, 2004. – 292 с.	2004
3	Ванторин В.Д. Механизмы приборных и вычислительных систем: Учебное пособие. – М.: Высш. шк., 1999. – 415 с.	1999