Соединение фаз системы между собой (рис. 1б)) придает ей особые качества, благодаря которым многофазные системы ( в особенности трехфазные) получили исключительное распространение в области передачи и преобразования электрической энергии. Одним из очевидных преимуществ связанной системы (рис. 1) является сокращение с шести до четырех числа проводников, соединяющих источники с нагрузкой. При благоприятных обстоятельствах это число может быть уменьшено до трех. В дальнейшем мы отметим целый ряд других преимуществ, которым обладают связанные системы.
Под симметричной многофазной системой ЭДС, напряжений или токов
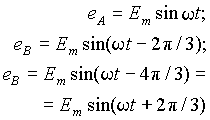 |
Û | 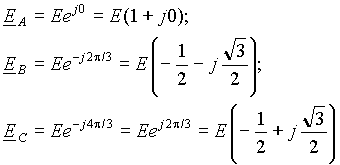 |
(1) |
Аналогичные выражения можно написать и для токов и падений напряжения в симметричной трехфазной системе.
Основное свойство
Многофазная система симметрична только тогда, когда в ней симметричны ЭДС, токи и напряжения. Если принять равными нулю внутренние сопротивления источников питания или включить их значения в сопротивления нагрузки, то условие симметрии системы сводится к симметрии ЭДС и равенству комплексных сопротивлений нагрузки. Это условие для трехфазной системы записывается в виде
| Z a = Z b = Z c . | (2) |
В дальнейшем мы будем считать, что источники питания являются источниками ЭДС и использовать условия симметрии системы в виде выражений (1) и (2).
В многофазные системы объединяют источники ЭДС и нагрузки. Для обеспечения правильного соотношения сдвига фаз при соединения или связывании системы в общем случае необходимо определить выводы элементов, по отношению к которым выполняются условия (1).
Они называются начало и конец фазы источника или нагрузки. Для источников многофазной системы принято за положительное направление действия ЭДС от начала к концу.
На электрических схемах, если это необходимо, начало и конец обозначают буквами латинского алфавита. На рис. 1 а) начала элементов соответствуют индексам XYZ , а концы — ABC . В дальнейшем мы будем использовать строчные буквы для нагрузки, а прописные для источников ЭДС.
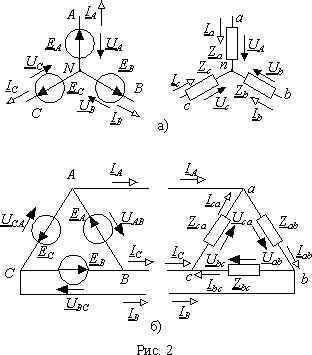 Существуют два способа связывания элементов в многофазную систему — соединение звездой и соединение многоугольником. Звезда это такое соединение, в котором начала всех элементов объединены в один узел, называемый нейтральной точкой . Подключение к системе при этом осуществляется концами элементов (рис. 2 а)).
Существуют два способа связывания элементов в многофазную систему — соединение звездой и соединение многоугольником. Звезда это такое соединение, в котором начала всех элементов объединены в один узел, называемый нейтральной точкой . Подключение к системе при этом осуществляется концами элементов (рис. 2 а)).
Многоугольник это соединение, в котором все элементы объединены в замкнутый контур так, что у соседних элементов соединены между собой начало и конец . С системой многоугольник соединяется в точках соединения элементов. Частным случаем многоугольника является треугольник рис. 2 б).
линейными проводами
фазными
u AB
|
U AB = U A —U B ; U BC = U B —U C ; U CA = U C —U A . |
(3) |
Построим векторную диаграмму для симметричной трехфазной системы фазных и линейных напряжений (рис. 3).
В теории трехфазных цепей принято направлять вещественную ось координатной системы вертикально вверх.
Каждый из векторов линейных напряжений представляет собой сумму одинаковых по модулю векторов фазных напряжений ( U ф = UA = UB =UC ), смещенных на угол 60° . Поэтому линейные напряжения также образуют симметричную систему и модули их векторов (U л = UAB = UBC =UCA ) можно определить как ![]() .
.
векторы линейных напряжений
любой произвольной системе линейных напряжений соответствует бесчисленное множество фазных
Из уравнений Кирхгофа для узлов a , b и c нагрузки соединенной треугольником (рис. 2 б)) можно представить комплексные линейные токи через фазные в виде
| I A = I ab —I ca ; I B = I bc —I ab ; I C = I ca —I bc . | (4) |
I A
Перейдем теперь к рассмотрению конкретных соединений трехфазных цепей.
U A
|
I a = U A /Z a ; I b = U B /Z b и I c = U C /Z c . |
(5) |
Ток в нейтральном проводе можно определить по закону Кирхгофа для нейтральной точки нагрузки. Он равен
| I N =I a +I b +I c . | (6) |
Z a
При симметричной нагрузке токи во всех фазах одинаковы и смещены по отношению друг к другу на 120° . Их модули или действующие значения можно определить как I = U ф /Z .
Векторные диаграммы для симметричной и несимметричной нагрузки в системе с нейтральным проводом приведены на рис. 4 б) и в).
I a
При несимметричной нагрузке между нейтральными точками источника и нагрузки возникает падение напряжения. Его можно определить по методу двух узлов, перестроив для наглядности схему рис. 5 а).
В традиционном для теории электрических цепей начертании она будет иметь вид рис. 5 б).
Отсюда
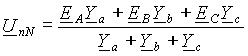 , , |
(7) |
где Y a =1/Z a , Y b =1/Z b , Y c =1/Z c — комплексные проводимости фаз нагрузки.
U nN
| U a = U A —U nN ; U b = U B —U nN ; U c = U C —U nN . | (8) |
Токи в фазах нагрузки можно определить по закону Ома
| I a = U a /Z a ; I b = U b /Z b ; I c = U c /Z c . | (9) |
Векторные диаграммы для симметричной и несимметричной нагрузки приведены на рис. 6. Диаграммы симметричного режима (рис. 6 а)) ничем не отличаются от диаграмм в системе с нулевым проводом.
U AB
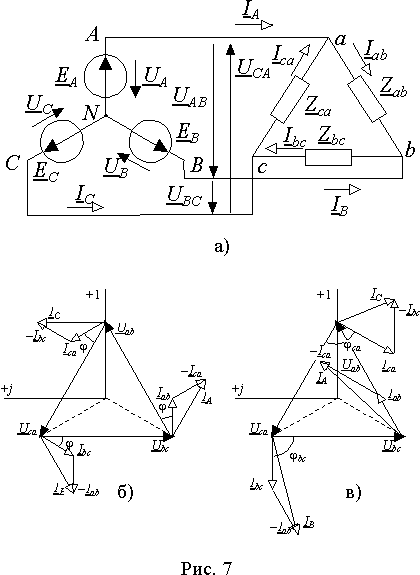 В трехфазных цепях нагрузка и источник могут быть соединены по-разному. В частности нагрузка, соединенная треугольником, может быть подключена к сети, в которой источник питания соединен звездой (рис. 7 а)).
В трехфазных цепях нагрузка и источник могут быть соединены по-разному. В частности нагрузка, соединенная треугольником, может быть подключена к сети, в которой источник питания соединен звездой (рис. 7 а)).
При этом фазы нагрузки оказываются подключенными на линейные напряжения
U ab = U AB ; U bc =U BC ; U ca = U CA .
Токи в фазах можно найти по закону Ома
I ab = U ab /Z ab ; I bc = U bc /Z bc ;
I ca = U ca /Z ca ,
а линейные токи из уравнений Кирхгофа для узлов треугольника нагрузки
| I A = I ab —I ca ; I B = I bc —I ab ; I C = I ca —I bc . | (10) |
Векторы фазных токов нагрузки на диаграммах для большей наглядности принято строить относительно соответствующих фазных напряжений. На рис. 7 б) векторные диаграммы построены для случая симметричной нагрузки. Как и следовало ожидать, векторы фазных и линейных токов образуют симметричные трехфазные системы.
На рис. 7 в) построена векторная диаграмма для случая разных типов нагрузки в фазах. В фазе ab нагрузка чисто резистивная, а в фазах bc и ca индуктивная и емкостная. В соответствии с характером нагрузки, вектор I ab совпадает по направлению с вектором U ab ; вектор I bc отстает, а вектор I ca опережает на 90° соответствующие векторы напряжений. После построения векторов фазных токов можно по выражениям (10) построить векторы линейных токов I A , I B и I C .
Трехфазная цепь является совокупностью трех однофазных цепей, поэтому ее мощность может быть определена как сумма мощностей отдельных фаз.
При соединении звездой активная мощность системы будет равна
|
P = P a + P b + P c = U a I a cosja + U b I b cosjb + U c I c cosjc = = I a 2 R a + I b 2 R b + I c 2 R c , |
(11) |
а реактивная
|
Q = Q a + Q b + Q c = U a I a sinja + U b I b sinjb + U c I c sinjc = = I a 2 X a + I b 2 X b + I c 2 X c . |
(12) |
Если нагрузка соединена треугольником, то активная и реактивная мощности будут равны
|
P = P ab + P bc + P ca = U ab I ab cosjab + U bc I bc cosjbc + U ca I ca cosjca = = I ab 2 R ab + I bc 2 R bc + I ca 2 R ca , |
(13) |
|
Q = Q ab + Q bc + Q ca = U ab I ab sinjab + U bc I bc sinjbc + U ca I ca sinjca = = I ab 2 X ab + I bc 2 X bc + I ca 2 X ca . |
(14) |
Полную мощность можно определить из треугольника мощностей как
| |
(15) |
полная мощность трехфазной цепи не является суммой полных мощностей фаз
При симметричной нагрузке мощности всех фаз одинаковы, поэтому полная мощность и ее составляющие для соединения звездой будут равны
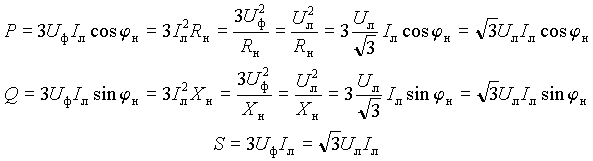 |
(16) |
При соединении нагрузки треугольником
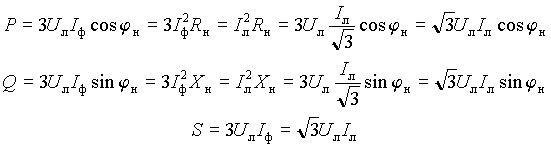 |
(17) |
Из выражений (16) и (17) следует, что полная мощность трехфазной сети и ее составляющие при симметричной нагрузке могут быть определены по линейным токам и напряжениям независимо от схемы соединения .
мгновенная мощность
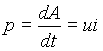 , , |
(1) |
где u и i — мгновенные значения напряжения и тока.
средней мощности
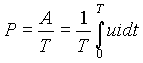 . . |
(2) |
Пусть u =U m sinwt и I m sin(wt -j ), тогда средняя мощность будет равна
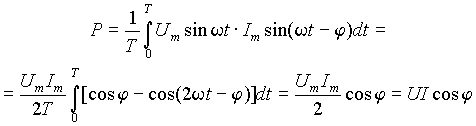 |
(3) |
т.к. интеграл второго слагаемого равен нулю. Величина cos jназывается коэффициентом мощности .
проблема cos
Выражение (3) можно представить также с помощью понятий активных составляющих тока I а и напряжения U а в виде
| P = UI cosj = U (I cosj ) = UI а = I (U cosj ) = IU а . | (4) |
Учитывая, что активные составляющие тока и напряжения можно выразить через резистивную состаляющую комплексного сопротивления цепи как I а =U /R или U а =IR , выражение (4) можно записать также в форме
| P = I 2 R = U 2 /R . | (5) |
активной мощностью
Выделим подинтегральную функцию выражения (3)
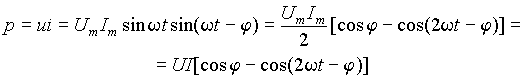 |
(6) |
Отсюда следует, что мгновенная мощность изменяется с двойной частотой сети относительно постоянной составляющей UI cosj равной средней или активной мощности.
При cosj = 1 (j = 0) , т.е. для цепи, обладающей чисто резистивным сопротивлением
| |
(7) |
Временные диаграммы, соответствующие этому случаю приведены на рис. 1 а).
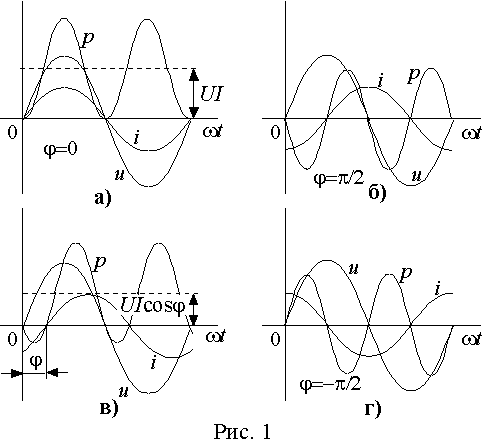
при резистивной нагрузке вся энергия поступающая от источника преобразуется в ней в тепло
При cosj = 0 (j = ±p /2) , т.е. для чисто реактивной цепи
| |
(8) |
в цепи не происходит преобразования энергии.
В общем случае произвольной нагрузки 1 > cosj > 0 ( 1< |j | < p /2) и
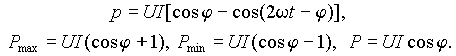 |
(8) |
преобладает процесс преобразования электрической энергии в тепло или механическую работу
Рассмотрим энергетические процессы в последовательном соединении rLC (рис. 2).
Падение напряжения на входе цепи уравновешивается суммой падений напряжения на элементах u =ur +uL +uC . Мгновенная мощность в цепи равна
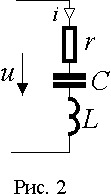 ui =ur i +uL i +uC i ui =ur i +uL i +uC i |
(9) |
Пусть напряжение и ток на входе равны u =U m sinwt и I m sin(wt -j ).
Тогда падения напряжения на элементах будут ur = rI m sin(wt -j ), uL = wLI m sin(wt -j +p /2) = xL I m sin(wt -j +p /2), uC = I m sin(wt -j -p /2)/(w C) = xC I m sin(wt -j -p /2).
Подставляя эти выражения в (9), получим
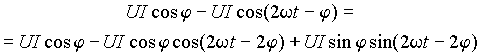 |
(10) |
реактивной мощностью
Реактивную мощность также можно представить через реактивные составляющие тока или напряжения
| Q = UI sinj = U (I sinj ) = UI р = I (U sinj ) = IU р . | (11) |
реактивная мощность положительна при
Из условия равенства переменных составляющих левой и правой частей уравнения (10) можно найти связь между P , Q и S = UI в виде
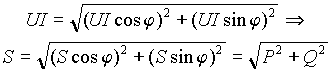 |
(12) |
полной или кажущейся мощностью
Таким образом, полная мощность это максимально возможная активная мощность, т.е. мощность, выделяющаяся в чисто резистивной нагрузке (cosj = 0).
Именно эта мощность указывается в паспортных данных электрических машин и аппаратов.
Реактивные составляющие токов и напряжений можно представить через активные и реактивные составляющие комплексного сопротивления, тогда для составляющих мощности
|
P = UI а = I 2 R = U а I = U 2 /R = U 2 G ; Q = UI р = I 2 X = U р I = U 2 /X = U 2 B ; S = UI = I 2 Z = U 2 /Z = U 2 Y. |
(13) |
Треугольник мощностей можно описать также с помощью комплексных чисел и изобразить векторами на комплексной плоскости в виде
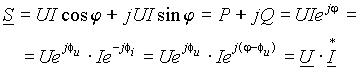 , , |
(14) |
где S — комплексная полная мощность, ![]() — сопряженный комплексный ток.
— сопряженный комплексный ток.
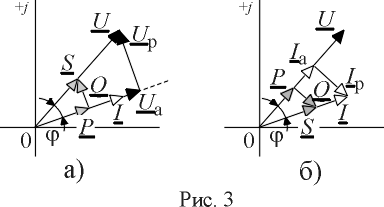 Пользуясь представлением активной и реактивной составляющих мощности через активные и реактивные составляющие токов и напряжений (выражения (4) и (11)), треугольник мощностей можно построить в двух вариантах (рис. 3 а) и б)).
Пользуясь представлением активной и реактивной составляющих мощности через активные и реактивные составляющие токов и напряжений (выражения (4) и (11)), треугольник мощностей можно построить в двух вариантах (рис. 3 а) и б)).
В первом случае активная и реактивная составляющие полной мощности выражаются через активную и реактивную составляющие напряжения U и треугольник мощностей получается изменением масштаба треугольника напряжений (рис. 3 а)).
Во втором случае (рис. 3 б)), построение выполнено с помощью активной и реактивной составляющих тока I .
Очевидно, что все виды мощности имеют одинаковую размерность, поэтому для их отличия от активной мощности, измеряемой в ваттах [Вт], для полной мощности введена единица, называемая вольт-амперы [ВА], а для реактивной мощности — вольт-амперы реактивные [ВАр]
 Выражение для активной мощности P = UI cosj позволяет определить коэффициент мощности с помощью ваттметра, вольтметра и амперметра.
Выражение для активной мощности P = UI cosj позволяет определить коэффициент мощности с помощью ваттметра, вольтметра и амперметра.
Для этого на вход цепи включают приборы по схеме рис. 4 и по их показаниям определяют коэффициент мощности в виде
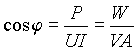 ,
,
где W, V и A — показания соответственно ваттметра, вольтметра и амперметра действующих значений. Из этого выражения можно также определить угол сдвига фаз j между током и напряжением на входе двухполюсника.
·Обзорные статьи
·Промо-статьи
·Презентации
·Качество электроэнергии
·Учебные пособия по электротехники для самостоятельного изучения
·Рефераты по электротехнике и радиоэлектронике
Учебное пособие по курсу электротехники
Электрические микромашины. Курс лекций
Общая Электротехника. Учебное пособие
Сборник лекций по теоретическим основам электротехники
Карта сайта
