Содержательный , который мы рассматривали ранее, измеряет ее количество, как уменьшение неопределенности наших знаний.
Однако любое техническое устройство не способно воспринимать непосредственно содержание информации, оно лишь понимает наличие или отсутствие электрических сигналов. Вследствие чего в вычислительной технике вынуждены использовать другой подход к оценке количества информации, который называется алфавитным.
Принцип алфавитного подхода к оценке количества информации
Алфавитный подход строится на принципе, утверждающем, что любое сообщение можно представить в виде кодов с помощью конечной последовательности , содержащейся в любом алфавите . Носители информации содержат любые последовательности символов, которые могут храниться, передаваться и обрабатываться как с помощью человека, так и с помощью технических устройств, в частности компьютера. Этот подход описал А.Н. Колмогоров, согласно которому, информативность, заключающаяся в последовательности символов, не может зависеть от содержания самого сообщения, а может определяться лишь минимальным количеством символов, необходимых для ее кодирования. Подобный подход к оценке количества информации носит объективный характер, так как не зависит от получателя, принимающего сообщения. Смысл же сообщений может учитываться только на этапе выбора алфавита кодирования либо не учитываться совсем.
Готовые работы на аналогичную тему
В основу принципа этого подхода лег подсчет числа символов в сообщении, таким образом, важна только длина сообщения и совсем не учитывается его содержание. Однако на длину сообщения может влиять мощность алфавита используемого языка.
Самый простой способ разобраться в этом — рассмотреть пример любого текста, написанного на каком-нибудь языке. Для нас, конечно же, удобным будет текст на русском языке.
Мощность алфавита и информационная емкость. Формула Хартли
алфавитом
Таким образом, алфавит — это множество символов, используемых при записи текста.
Мощность (размер) алфавита — это полное количество символов в алфавите.
Мощность алфавита обозначается буквой $N$.
Например:
-
мощность алфавита, состоящего из русских букв (кириллицы), равна $33$;
-
мощность алфавита, состоящего из латинских букв — $26$;
12 стр., 5670 словИнформация: понятия, виды, получение, измерение и проблема обучения
... невозможно построение информационного общества. Основные свойства информации (и сообщений): полнота (содержание всего необходимого для понимания информации); актуальность (необходимость) и значимость (сведений, знаний); ясность (выразительность сообщений на языке интерпретатора); адекватность, точность, ...
-
мощность алфавита текста набранного с клавиатуры компьютера равна $256$ (строчные и прописные латинские и русские буквы, цифры, знаки арифметических операций, скобки, знаки препинания и т.д.);
-
мощность двоичного алфавита равна $2$.
При алфавитном подходе считают, что каждый символ текста несет в себе определенную информационную емкость, которая, в свою очередь, зависит от мощности алфавита.
Алфавит, с помощью которого записывается сообщение, состоит из $N$ знаков. В самом простом случае при длине кода сообщения, равной одному знаку, отправитель может послать одно из $N$ возможных сообщений, которое будет нести количество информации, равное $I$, согласно формуле:
$N = 2^I$ ,
где $N$ — количество знаков в алфавите знаковой системы,
$I$ — количество информации, которое несет каждый знак.
Данную формулу вывел Р. Хартли, который в $20$-е годы прошлого столетия заложил основы теории информации, в которой определялась мера количества информации при решении некоторых задач.
Хартли утверждал, что на количество информации, содержащейся в сообщении, может влиять фактор неожиданности, который, в свою очередь, зависит от вероятности получения сообщения. Если эта вероятность получения сообщения высокая, а неожиданность при этом низкая, то сообщение будет содержать мало полезной для человека информации.
Например, с помощью приведенной формулы можно определить количество информации, которое несет знак в двоичной системе счисления:
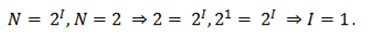
Рисунок 1.
Информационная емкость знака двоичной системы составляет 1 бит.
Пример 1
Необходимо определить информационную емкость буквы русского алфавита (без учета буквы «ё»).
Решение:
Представим себе, что текст к нам поступает последовательно, по одному знаку, словно бумажная лента, выползающая из телеграфного аппарата. Предположим, что каждый символ, который появляется на ленте, с равной вероятностью может быть любым символом алфавита. В действительности это не совсем так, но для упрощения примем такое предположение.
В каждой очередной позиции текста может появиться любой из $N$ символов. Тогда, согласно известной нам формуле, каждый такой символ несет количество информации равное $I$ бит, которое можно определить из решения уравнения:
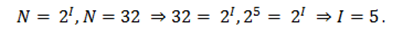
Рисунок 2.
Информационная емкость буквы русского алфавита составляет $5$ бит информации.
Таким образом, формула определения $N$ связывает между собой количество возможных событий и количество информации, которое содержит в себе полученное сообщение. В рассматриваемой выше задаче $N$ — это количество знаков в русском алфавите, а $I$ — количество информации, которое несёт одна буква.
Маркировка товаров как носитель информации для потребителя
... нормативно и актами-техническими документами на конкретные виды группы на или продукции. Информация рекламного характера в маркировки составе должна соответствовать законодательству Российской ... достоверность на маркировке сведения не должны вводить потребителя и получателя в заблуждение относительно количества, качества, страны, изготовителя происхождения; использование для маркировки красителей ...
Сообщение состоит из последовательности знаков, каждый из которых несет определенное количество информации.
Количество информации в сообщении можно определить, используя формулу:
$I_c = K \cdot I$,
где $I_c$ — количество информации, содержащееся в сообщении;
- $I$ — количество информации, которое несет один знак (информационная емкость);
- $K$ — количество знаков в сообщении.
Рассмотрим пример решения задачи
При измерении информации удобным является использование размера алфавита $N$, равного целой степени двойки. К примеру, если $N=16$, то это означает, что каждый символ несет $4$ бита информации, так как $2^4= 16$.
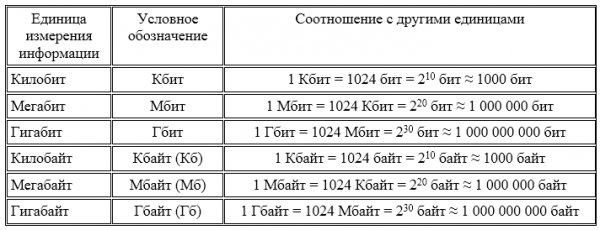
Единицы измерения информации
Ограничений максимального размера алфавита теоретически не существует. Однако существует алфавит, который можно назвать достаточным. Он используется при работе с компьютером. Мощность этого алфавита — $256$ символов. Он включает в себя практически все необходимые символы: латинские и русские буквы, цифры, знаки арифметических операций, всевозможные скобки, знаки препинания.
Поскольку $256 = 2^8$, то отсюда следует, что $1$ символ этого алфавита содержит $8$ бит информации. Эта величина лежит в основе использования вычислительной технике и носит название — байт .
$1$ байт = $8$ бит
Используя данный алфавит, который еще называется таблицей ASCII-кодов, можно легко подсчитать объем информации в тексте. В данном случае $1$ символ алфавита содержит в себе $1$ байт информации, поэтому необходимо просто определить количество символов, то число, которое получим в результате, и будет выражать информационный объем текста в байтах.
Допустим небольшая книга, распечатанная на принтере, содержит $50$ страниц, при этом на каждой странице расположено $50$ строк, в каждой строке — $60$ символов.
Проведем несложный расчет и получим, что страница содержит:
$50 \cdot 60 = 3000$ байт информации.
Объем же информации, содержащейся в книге:
$3000 \cdot 50 = 150 \ 000$ байт.
Любая система единиц измерения содержит основные единицы и от них.
При измерении больших объемов информации на практике широко используются следующие производные от байта единицы, которые приведены в таблице: