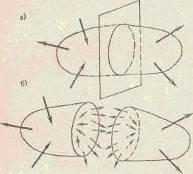Механические свойства твердых тел в практике

метки: Деформация, Конструкция, Материал, Здание, Строительство, Сооружение, Прочность, Бетон

Данную тему для реферата я выбрала потому, что она связана с моей будущей профессией. И эту же тему мы затрагивали в курсе физики. Поэтому я решила более подробно рассмотреть виды деформации и способы ее учета. Также стало интересно, какие материалы используются в строительстве, и какими качествами они должны обладать. Мне захотелось узнать, как выбирают форму детали, из которой в последующем делают различные изделия.

1.Механические свойства твёрдых тел.

1.1.Виды деформации.

Виды деформации тел. Механические свойства твёрдых тел обусловлены их молекулярной структурой. Внешнее механическое воздействие на тело может приводить к изменению его формы и объёма, т.е. к деформации.

Деформация – изменение формы и размера твёрдого тела под действием внешних сил.

Различают два вида деформаций – упругую и пластическую.

Упругая деформация – деформация, сохраняющаяся после прекращения действия внешней силы.

Упруго деформируются резина, сталь, человеческое тело, кости и сухожилия.

Пластическая деформация – деформация, сохраняющаяся после прекращения действия внешней силы.

Пластичны свинец, алюминий, воск, пластилин, замазка, жевательная резинка.

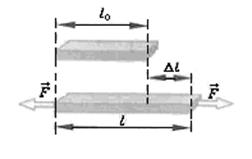
Упругая деформация. Модуль Юнга. Рассмотрим упругую деформацию (растяжение) стержня, длина которого l ₀ , а площадь поперечного сечения S, под действием внешней силы F (рис.1).

Деформация стержня прекращается тогда, когда сила упругости становится равной внешней силе. Согласно закону Гука

F _упр =kΔl,

где Δl – абсолютное удлинение стержня.

Чтобы добиться аналогичного абсолютного удлинения Δl стержня двойного сечения, требуется вдвое большая сила, поэтому для характеристики упругих свойств тела вводится механическое напряжение.

Механическое напряжение – физическая величина, равная отношению силы упругости к площади поперечного сечения тела:

σ = F _упр /S. (1)

механическое напряжение измеряется в паскалях (Па).

Рис.1. Упругая деформация стержня

Более удобной величиной чем абсолютное удлинение является относительное удлинение.

Относительное удлинение равно отношению абсолютного удлинения тела к его первоначальной длине:

ε=|Δl|/l ₀ . (2)

Относительное удлинение показывает, какую часть первоначальной длины l ₀ тела составляет его абсолютное удлинение.

Выражая F _упр и l₀ из равенств (1) и (2) и подставляя их в закон Гука, получаем

σ=(kl ₀ /S)ε.

Коэффициент пропорциональности (kl ₀ /S) между напряжением σ и относительным удлинением ε называется модулем упругости (или модулем Юнга):

E=kl ₀ /S.

Модуль Юнга измеряется в паскалях (Па).

В отличие от жёсткости k, характеризующей только данный стержень, модуль упругости E характеризует вещество, из которого он сделан (табл.1).

Таблица 1

Модуль Юнга для некоторых металлов

Вещество	E,Па
Pb	0.16*10 11
Al	0.7*10 11
Cu	1.1*10 11
Fe	1.9*10 11
Ni	2.1*10 11
W	3.6*10 11

Закон Гука

При упругой деформации тела механическое напряжение прямо пропорционально относительному удлинению тела:

σ=Eε. (3)

при растяжении твёрдого тела сила упругости сжимает образец. Она возникает потому, что при увеличении межатомного расстояния по сравнению с равновесным атомы притягиваются друг к другу. Результирующая сила притяжения атомов после прекращения действия внешней силы сжимает образец до первоначальной длины.

Закон Гука справедлив лишь при малой деформации, т.е. при малом относительном удлинении ε.

Пластическая деформация. Предел прочности. Начиная с некоторого значения ε _max деформация перестаёт быть упругой, становясь пластической.

Предел упругости – максимальное напряжение в материале, при котором деформация ещё является упругой.

Пластичные материалы – материалы, которые не разрушаются при напряжении, значительно превышающем предел упругости.

Благодаря пластичности алюминий, медь, сталь можно подвергать различной механической обработке: штамповке, ковке, изгибу, растяжению. При дальнейшем увеличении деформации материал разрушается.

Предел прочности – максимальное напряжение, возникающее в теле до его разрушения.

При сжатии стержня межатомные расстояния уменьшаются. Результирующая сила отталкивания атомов препятствует сжатию. Более резкое возрастание сил отталкивания (при сжатии образца) по сравнению с силами притяжения (при его расширении) объясняется различие пределов прочности при растяжении и сжатии, приведённых для ряда материалов в таблице 2.

Таблица 2

Предел прочности при растяжении и сжатии

материал	Растяжение , МПа	Сжатие, МПа
Бетон	4	30-40
Кирпич	5,5	10-21
Мрамор	10	110
Гранит	20	240
Железо	170	650
Кость	110	150

Атомы и молекулы в твёрдых телах совершают тепловые колебания около равновесных положений, в которых энергия минимальна. При уменьшении расстояний между атомами возникают силы отталкивания, а при увеличении расстояний между ними – силы притяжения. Это и обуславливает механическую прочность твёрдых тел, т.е. их способность противодействовать изменению формы и объёма. Растяжению тел препятствуют силы межатомного притяжения, а сжатию – силы отталкивания. Этими же силами объясняются упругие свойства твёрдых тел.

Недеформируемых тел в природе не существует. В то же время часто приходится иметь дело со столь малыми деформациями, что их трудно обнаружить. Например, если наступить на кирпич, то его высота уменьшится примерно на 1/20000 см. При такой деформации соседние атомы сближаются примерно на 2*10 ^-14 см!

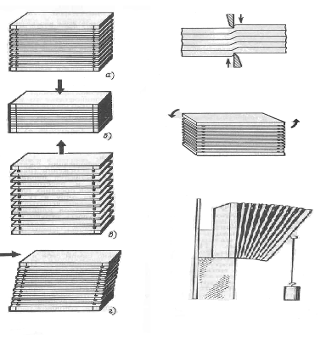
Среди деформаций, возникающих в твёрдых телах, можно выделить пять основных видов: растяжение, сжатие, сдвиг, кручение и изгиб. Для демонстрации этих видов деформаций можно воспользоваться моделью, состоящей из нескольких пластин, скрепленных пружинами (рис. 2, а).

Каждая пластина изображает слой атомов (молекул) в кристаллической решетке, пружины моделируют действие сил связи.

При деформации сжатия (рис.2, б) и растяжения (рис.2, в) пластины остаются параллельными друг другу и расстояния между каждой парой соседних пластин на одну и ту же величину. Растяжение испытывают тросы подъёмных кранов, струны музыкальных инструментов. Сжатию подвергаются колонны, стены и фундаменты зданий.

Деформацию сдвига можно получить, смещая верхнюю пластину параллельно самой себе и удерживая нижнюю неподвижной. При этом все пластины сместятся так, что расстояния между ними останутся неизменными (рис.2, г).

Деформацию сдвига испытывают, например, заклёпки и болты, соединяющие металлические конструкции. Деформацией сдвига сопровождается процесс разрезания ножницами бумаги, листового железа (рис.3).

Деформацию кручения можно наблюдать при повороте верхней пластины модели вокруг вертикальной оси (рис. 4).

При этом расстояния между пластинами не меняются, но точки платин, ранее лежавшие на одной прямой, смещаются в сторону друг от друга. Деформации кручения возникают при завинчивании гаек, при работе валов машин, при сверлении металлов и т.д.

Деформацию изгиба можно наблюдать, закрепив один конец балки, а к другому подвесив груз. В опыте на модели (рис. 5) хорошо видно, что деформация изгиба сводится к деформации сжатия и растяжения, различной в разных частях тела. В середине бруска существует слой, не подвергающийся ни растяжению, ни сжатию. Он называется нейтральным слоем.

Поскольку слои, близкие к нейтральному, испытывают меньшую деформацию, то детали машин и конструкций, работающие на изгиб, выгодно делать полыми. Замена сплошных стержней и брусков трубами или балками, даёт экономию материала и значительно снижает массу (и вес) конструкций без ухудшения их механических свойств.

В результате длительной эволюции кости животных и птиц приобрели трубчатое строение. Это значительно облегчает расчёт механических свойств конструкций и деталей машин.

Деформация и напряжение. Деформацию сжатия и растяжения можно характеризовать абсолютным удлинением Δl, равным разности длин образца после растяжения l и до него l ₀ :

Δl=l-l ₀ . (4)

Абсолютное удлинение Δl при растяжении положительно, при сжатии отрицательно.

Отношение абсолютного удлинения Δl к первоначальной длине образца l ₀ называют относительным удлинением ε:

ε=|Δl|/l ₀ . (5)

Рис.3

Рис.5

Рис.4

Рис.2

Физическая величина, равная отношению модуля силы упругости F , возникающей при деформации, к площади сечения S образца, перпендикулярного вектору силы F, называется механическим напряжением σ:

σ=F/l. (6)

За единицу механического напряжения в СИ принята единица паскаль (Па): 1 Па=1 H/м ² .

Модуль упругости. Деформация называется упругой, если после прекращения действия силы размеры и форма тела восстанавливаются. Неупругая деформация называется пластической. При малых (упругих) деформациях растяжения и сжатия отношение механического напряжения σ к относительному удлинению ε называется модулем упругости E (модулем Юнга).

Эта величина одинакова для образцов любой формы и размеров, изготовленных из данного материала:

E=σ/ε= (Fl ₀ )/(|Δl|S).

(7)

Модуль упругости E характеризует механические свойства материала независимо от конструкции изготовленных из него деталей. Поскольку относительное удлинение – отвлечённое число, то модуль упругости выражается в тех же единицах, что и механическое напряжение.

Диаграмма растяжения. Зависимость относительного удлинения образца от приложенного к нему напряжения является одной из важнейших характеристик механических свойств твёрдых тел. Графическое изображение этой зависимости называется диаграммой растяжения. По оси ординат откладывается механическое напряжение σ, приложенное к образцу, а по оси абсцисс – относительное удлинение ε (рис. 6).

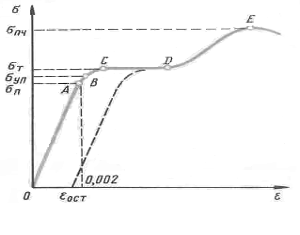
При небольших напряжениях относительное удлинение прямо пропорционально напряжению, а после снятия нагрузки размеры тела полностью восстанавливаются. Такая деформация, как уже говорилось, называется упругой. Максимальное напряжение σ _n , при котором деформация ещё остаётся, называется пределом пропорциональности (точка А).

Если ещё увеличить нагрузку, то деформация становится линейной, напряжение перестаёт быть прямо пропорциональным относительному удлинению. Тем не менее при небольших нелинейных деформациях после снятия нагрузки форма и размеры тела практически восстанавливаются (участок АВ диаграммы).

Максимальное напряжение, при котором ещё не возникают заметные остаточные деформации, называют пределом упругости σ _уп . Предел упругости превышает предел пропорциональности лишь на сотые доли процента.

При напряжениях, превышающих предел упругости σ _уп , образец после снятия нагрузки не восстанавливает свою форму или первоначальные размеры. Такие деформации называют остаточными или пластическими.

В области пластической деформации (участок ВС) деформация происходит не пропорционально увеличению напряжения. На горизонтальном участке CD материал «течёт» — деформация возрастает при неизменном напряжении. Напряжение σ _т (ордината точки C), при котором материал «течёт», называют пределом текучести.

Если в области пластических деформаций снять напряжение с тела, то его размеры не будут равны первоначальным. Разгрузка изображается пунктирной кривой на диаграмме рисунка 6. У тела сохраняется остаточная деформация ε _ост .

Материалы, у которых область текучести CD значительна, могут без разрушения выдерживать большие деформации. Такие материалы называют пластичными. Пластичны пластилин, медь, золото. Если же область текучести материала почти отсутствует, он без разрушения может выдержать лишь небольшие деформации. Такие материалы называют хрупкими. Примерами хрупких материалов могут служить стекло, кирпич, бетон, чугун.

Материал в процессе деформации может упрочниться. В этом можно убедиться при сгибании толстого медного прута или пластины. Для того чтобы разогнуть образец, требуются заметно большие усилия, чем для его сгибания. Это явление называется наклепом.

После точки E кривая идёт вниз, это значит, что дальнейшая деформация вплоть до разрыва происходит при всё меньшем напряжении. Наибольшее напряжение σ _пч , которое способен выдержать образец без разрушения, называется пределом прочности.

Запас прочности. Для того чтобы машины и различные сооружения, здания, мосты были надёжными, при их проектировании конструкторы учитывают необходимый запас прочности. Очевидно, что все эти сооружения должны работать в области упругих деформаций.

Коэффициентом безопасности (или запасом прочности) называется отношение предела пропорциональности σ _n данного материала к максимальному напряжению σ_д , которое будет испытывать деталь конструкции в работе:

n=σ _n /σ_д . (8)

В зависимости от необходимой надёжности различных деталей и конструкций коэффициент безопасности выбирают обычно в пределах от 2 до 10.

1.2.Основные допущения о свойствах материалов и характере деформирования

Расчет конструкций и их элементов с учетом всего многообразия физико-механических свойств реальных материалов является или теоретически невозможным, или практически неприемлемым по своей сложности. Поэтому, отказываясь от принятой в теоретической механике модели абсолютно твердого тела, в сопротивлении материалов приходится вводить свою модель — модель идеализированного деформируемого тела. Однако для решения поставленной задачи необходимо сделать ряд допущений.

1-е допущение. Материал представляет собой однородную сплошную среду. Предположение об однородности позволяет отвлечься от структурных особенностей материала и считать, что любой объем, выделенный из тела (конструкции), воспринимает часть общей нагрузки, приходящейся на все тело (конструкцию).

Так, например, строительная сталь при нормальной температуре состоит из двух компонентов: феррита и цементита. Феррит — почти чистое железо, имеющее в небольшом количестве растворенный углерод и другие химические элементы, образует в стали хаотично ориентированные зерна 1 (рис. 7) площадью (2—6) 10 ³ мкм² . Цементит-карбид железа Fe₃ C — образует с ферритом смесь — перлит 2, заполняющую главным образом участки между зернами феррита. Работа стали зависит от соотношения этих двух компонентов. Чем меньше зерно, тем равномернее перлит распределен по объему стали, более упорядочена в среднем взаимная ориентация зёрен и тем больше оснований считать сталь однородным материалом, несмотря на неоднородность её микроструктуры.

Заведомо неоднороден такой материал, как бетон. Он состоит из бессистемно разбросанных зерен заполнителя (гравия, щебня, керамзита, шлака, песка и пр.) различной крупности и формы, которые скреплены цементной массой или другим вяжущим веществом. Но размеры бетонных элементов (как, впрочем, и стальных) велики по сравнению с размерами зерен, поэтому практически и бетон можно считать в среднем однородным (квазиоднородным).

Предположение об однородности материала неотделимо от понятия сплошной среды, т.е. среды, непрерывно (без пустот) заполняющей отведенный ей объем. Свойство непрерывности позволяет использовать в расчетах методы анализа бесконечно малых величин (дифференциальное и интегральное исчисления).

Обычно сплошную среду принимают изотропной, полагая, что физико-механические свойства любого выделенного из нее тела одинаковы по всем направлениям. Благодаря мелкозернистой структуре квазиизотропны макрообъемы стали, хотя отдельно взятые зерна феррита (микрообъемы) анизотропны.

В некоторых случаях предположение об изотропии неприемлемо. К анизотропным материалам относится древесина, прочность и деформативность которой зависят от направления усилия по отношению к расположению волокон. Анизотропны фанера и конструкционные пластические массы (стеклопластики, органическое стекло, винипласты, пенопласты, сотопласты, древесные пластики и др.), у которых изменчивость механических свойств обусловлена неоднородностью структуры и спецификой изготовления.

2-е допущение. Материал до известного предела нагружения работает упруго. Упругостью называется способность материальных тел восстанавливать первоначальную форму и размеры после снятия нагрузки. Деформации, полностью исчезающие после снятия нагрузки, называются упругими в отличие от пластических, или остаточных, которые не исчезают.

В большинстве задач сопротивления материалов среда условно считается абсолютно упругой. В действительности же реальные тела пусть в малой степени, но обнаруживают отступление от идеальной упругости. При больших нагрузках отступление становится столь существенным, что сплошная среда должна наделяться свойствами упругопластического материала.

В последнее время возросла актуальность расчёта строительных конструкций и их элементов с учетом развития пластических деформаций. Особенно это касается металлических конструкций и объясняется постоянным стремлением к снижению их материалоемкости и более рациональному использованию стального проката.

3-е допущение. Перемещения точек элемента (или системы элементов), обусловленные его деформацией, весьма малы по сравнению с размерами самого элемента. На основе этого допущения вводится принцип начальных размеров, согласно которому при составлении уравнений равновесия (уравнений статики) элемент или систему элементов рассматривают как недеформируемое тело, имеющее после нагружения те же геометрические размеры, что и до нагружения. Такой подход позволяет пренебречь изменениями в расположении внешних сил при деформировании реального тела. Он справедлив для жестких элементов и систем.

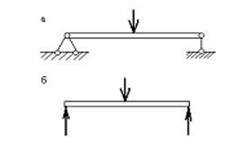
Пусть, например, к элементу, изображенному на рис. 8, подвешен груз F и требуется определить реактивный момент в заделке. По правилам теоретической механики, считающей тела недеформируемыми, m=Fl. В действительности же элемент деформируется(изгибается), точка приложения груза перемещается по вертикали и горизонтали, а момент в заделке m=Fl. Если элемент достаточно жесткий и, следовательно, деформируется мало, то можно пренебречь горизонтальным перемещением и определять момент по первой формуле, полагая l=l ₁ .

4-е допущение. Перемещения точек элемента(системы элементов) в упругой стадии работы материала пропорциональны силам, вызывающими эти перемещения. Системы, подчиняющиеся такой закономерности, называются линейно-деформируемыми (рис. 9).

Для них справедлив принцип независимости действия сил (принцип суперпозиции), который может быть сформулирован следующим образом: результат воздействия нескольких сил равен сумме результатов воздействия каждой силы, прикладываемой в отдельности, и не зависит от последовательности приложения. Этот принцип, широко используемый в теоретической механике, к деформируемым телам применим только при соблюдении трех предыдущих допущений. Он позволяет расчленять сложные задачи на более простые, решение которых известно или легко осуществимо. Иллюстраций может служить рис.10.

Перечисленные допущения являются в сопротивлении материалов основополагающими, но они не исчерпывают всевозможных приемов идеализации свойств материалов и характера деформирования изучаемых объектов. В дальнейшем при рассмотрении конкретных расчетно-теоретических вопросов будут вводиться и другие упрощения. При этом следует всегда иметь в виду, что успешное решение любой практической задачи зависит в первую очередь от умения отделить в реальной конструкции существенные факторы от второстепенных.

1.3.Геометрическая схематизация элементов строительных конструкций

Расчет любого сооружения, конструкции или отдельного конструктивного элемента начинается с выбора расчетной схемы. Она представляет собой упрощенную, идеализированную схему, которая отражает наиболее существенные особенности реального объекта, определяющие его поведение под нагрузкой.

Выбор расчётной схемы в сопротивлении материалов начинается со схематизации свойств материала и характера деформирования твёрдого тела. Вторым шагом является схематизация геометрической формы реального объекта. Формы элементов строительных конструкций весьма разнообразны, однако с достаточной степенью точности их можно отнести к четырём основным категориям.

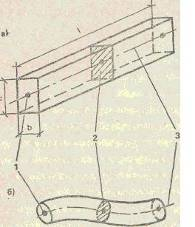
Брус- элемент, у которого один размер (длина l) значительно превышает два других. Геометрически его можно представить как тело, образованное путем перемещения плоской фигуры 2 вдоль некоторой линии 3, называемой продольной осью бруса (рис.11).

Центр тяжести 1 фигуры находится на этой оси, а сама фигура ей перпендикулярна и называется поперечным сечением бруса. Продольная ось, таким образом, является геометрическим местом центров тяжести поперечных сечений, поэтому при переходе от конструктивной схемы к расчётной в большинстве случаев можно не вычерчивать брус полностью, а ограничиться изображением только оси.

Рис.11	Рис.12
Рис.13

В зависимости от ее формы различают брусья прямые (см. рис. 11, а) и кривые (см. рис. 11,6).

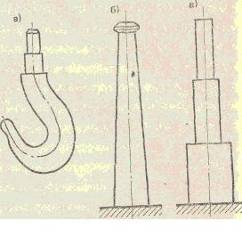
В строительных конструкциях более распространены прямые брусья. Примером кривого бруса может служить грузоподъемный крюк (рис. 12, а).

Прямой брус постоянного сечения называется призматическим (см. рис. 11, а).

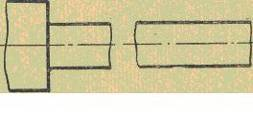
Встречаются также брусья с непрерывно меняющимся сечением (например, промышленные трубы, рис. 12,6) и ступенчатые (например, мостовые опоры, рис. 12, в).

В зависимости от конструктивного назначения среди брусьев различают стержни, балки (см. рис. 8; 9; 10) и колонны.

Оболочка — тело, ограниченное двумя криволинейными поверхностями, у которого длина и ширина b велики по сравнению с толщиной t (рис. 13, а).

Если при тех же соотношениях размеров тело ограничено параллельными плоскостями (рис. 13,6), то оно называется пластиной. К оболочкам относятся стенки сосудов для хранения жидкостей, газов и сыпучих материалов (стенки резервуаров, газгольдеров, бункеров и т.п.), листовые конструкции доменных цехов (кожух доменной печи, воздухонагревателей, пылеуловителя), купола и своды зданий. К пластинам могут быть отнесены плос­кие днища сосудов, настил рабочих площадок цехов, обшивка каркасных кровельных и стеновых панелей. Толстые пластины принято называть плитами.

Тела, у которых все три размера одного порядка, на­зываются массивами. К ним относятся фундаменты (рис. 13, б), подпорные стены и т. п.

Определение усилий и деформаций оболочек, пластин и массивов в большинстве случаев неосуществимо методами сопротивления материалов. Подобные задачи могут быть решены только с позиций теории упругости, основные предпосылки которой отличаются большей широтой и не ограничиваются такой формой тела, как брус.

1.4.Внешнее воздействие на тело

Классификация нагрузок.

Сооружения, конструкции и их элементы испытывают в процессе возведения и эксплуатации внешние воздействия. К ним относятся силовые воздействия от нагрузок, а также воздействия от изменения температуры, смещения опор, усадки и других подобных явлений, вы­зывающих реактивные силы.

Нагрузки классифицируют по разным признакам. По способу приложения они могут быть объемными или поверхностными. Объемные силы непрерывно распределены по всему объему, занимаемому элементом. К их числу относятся, например, сила тяжести и силы инерции. Нагрузка, приходящаяся на единицу объема, называет­ся интенсивностью объемной нагрузки. Она выражается в единицах силы, отнесенных к единице объема (Н/м ³ , кН/м³ и т.д.).

Если внешние силы являются результатом непосредственного взаимодействия элемента с другими телами (твердыми, жидкими или газообразными), то они прикладываются только по площадкам контакта и называются поверхностными. Сюда относятся: давление жидкости или газа на стенки сосуда, снеговая нагрузка на кровлю здания, ветровая нагрузка и др. Давление должно выражаться в единицах силы, отнесенных к единице площади (Н/м ² , кН/м² и т.д.).

Однако в СИ вводится специальная производная единица — паскаль: 1 Па = = 1 Н/м² , поэтому интенсивность поверхностной нагрузки р логично также выражать в паскалях и кратных ему единицах (кПа, МПа), но это не всегда удобно.

Поскольку соприкасание реальных, т.е. деформируемых тел, всегда происходит не в точке, а по некоторой, пусть даже очень малой, площадке, все поверхностные нагрузки являются распределенными. Однако в тех случаях, когда площадка контакта пренебрежимо мала по сравнению с размерами нагружаемого элемента, вводят понятие сосредоточенной силы F’ как равнодействующей давления по указанной площадке (например, сила, обусловленная давлением обода колеса на рельс, рис. 14)

В практических расчетах часто встречается нагрузка, распределенная по длине элемента конструкции. Так, например, на каждую промежуточную балку перекрытия здания (рис. 15, а) приходится полоса поверхностной нагрузки р шириной а (рис. 15,6).

Интенсивность нагрузки, распределенной по длине балки (рис. 15,0),

q = pa (9)

выражается в единицах силы, отнесенных к единице длины (Н/м, кН/м и т.д.).

В рассматриваемом случае интенсивность постоянна по длине, поэтому нагрузка называется равномерно распределенной и графически изображается в виде прямоугольника. Однако интенсивность может быть переменной и тогда нагрузка распределяется по более сложному закону: треугольному (например, при гидростатическом давлении — давлении покоящейся жидкости), трапецеидальному (нагрузка от собственного веса двускатных и односкатных балок), синусоидальному (нагрузка от ветрового напора на элементы типа оболочек) и т. п.

В процессе расчетной схематизации реальные нагрузки не всегда могут быть сведены лишь к сосредоточенным и распределенным силовым воздействиям. Возможны и моментные воздействия — в виде сосредоточенных моментов и моментов, распределенных по длине элемента или его поверхности. На рис. 16 показано, как появляются сосредоточенные моменты т ₁ , т₂ , и т₃ в результате замены бруса его продольной осью и приведения к ней поверхностных сил F₁ , F₂ и F₃ , приложенных в плоскости чертежа. Сосредоточенные моменты выражаются в единицах силы, умноженных на единицу длины (Нм, кНм и т.д.).

По характеру изменения в процессе приложения нагрузки делятся на статические, динамические и повторно-переменные. К статическим относятся нагрузки, не меняющиеся со временем (например, нагрузка от собственного веса) или меняющиеся настолько медленно, что вызываемые ими ускорения и силы инерции элементов конструкции пренебрежимо малы (например, снеговая нагрузка).

Динамические нагрузки в отличие от статических меняют свое значение, положение или направление в короткие промежутки времени (движущиеся нагрузки, ударные, сейсмические и др.), вызывая большие ускорения и силы инерции, что приводит к колебаниям конструкций и сооружений.

Повторно-переменными называются нагрузки, многократно (до нескольких миллионов раз) изменяющие со временем значение или значение и знак. Разрушение материала под действием таких нагрузок называется усталостным (например, разрушение куска проволоки от многократного перегибания, рис. 17), а способность противостоять ему— сопротивлением усталости.

По продолжительности действия нагрузки делят на постоянные и временные. К постоянным относятся нагрузки, действующие в течение всего времени существова­ния конструкции или сооружения (например, вес несущих и ограждающих конструкций, вес и давление грунта).

Временные нагрузки действуют на протяжении отдельных периодов эксплуатации или возведения объекта. К ним относятся нагрузки от веса людей, материалов и оборудования; давление жидкостей, газов и сыпучих материалов в сосудах и трубопроводах; атмосферные нагрузки (снеговая, ветровая, гололедная); температурные, монтажные, сейсмические, взрывные, аварийные и прочие воздействия ограниченной продолжительности.

1.5.Внутренние силы в поперечном сечении бруса

В недеформированном состоянии, т.е. при отсутствии внешних воздействий, связанность тела обусловлена силами взаимодействия атомов. Эти силы стремятся сохранить тело как единое целое, препятствуя любой попытке изменить взаимное расположение атомов и таким образом деформировать тело. Внешние воздействия, наоборот, стремятся вызвать деформирование тела путём изменения межатомных расстояний, взаимного расположения атомов и сил их взаимодействия. Однако если бы механика деформируемого тела ставила перед собой задачу изучать силы, действующие на каждый атом в отдельности, пользоваться её аппаратом было бы чрезвычайно трудно. Поэтому сопротивление материалов рассматривает поведение макрообъёмов материала, т.е. объёмов, состоящих из большого количества атомов и имеющих такие размеры, которые позволяют считать материал сплошным и однородным. Сплошное однородное тело не имеет в своём составе взаимодействующих частиц, и его целостность обеспечивают внутренние связи. Из теоретической механики известна так называемая аксиома связей, которая гласит: равновесие тела сохранится, если действие связей, закрепляющих тело в пространстве (рис.18,а), заменить их реакциями (рис.18,б).

Рис.18
	Рис.19

Применяя эту аксиому к деформируемому телу, можно мысленно рассечь его произвольной плоскостью (рис.19,а), отделить одну часть от другой и взамен нарушенных связей приложить к каждой части силы, равные усилиям связей (рис.19,б).

Такие силы называются внутренними. Они непрерывно распределяются по образовавшемуся сечению вследствие допущения о сплошности материала. Их находят посредством специального приёма – метода сечений, сущность которого заключается в следующем.

Пусть на тело, имеющее форму бруса, действует система взаимно уравновешенных внешних сил F ₁ ,F₂ ,…,F_n (рис.20, а).

Для определения

внутренних сил производят последовательно четыре операции: 1) рассекают брус в интересующем месте воображаемой плоскостью; 2) отбрасывают мысленно одну из образовавшихся частей (обычно ту, к которой приложено больше сил), в результате чего нарушается равновесие оставшейся части;

3) заменяют действие отброшенной части на оставшуюся внутренними силами f ₁ ,f₂ ,…,f_k (рис. 20, 6); 4) составляют уравнения равновесия всех сил, приложенных к оставшейся части. При этом имеют в виду, что внутренние силы согласно правилам теоретической механики могут быть приведены к центру тяжести сечения и, таким образом, заменены главным вектором R и главным моментом М (рис. 20, в).

Каждый из этих двух статических эквивалентов внутренних сил можно представить в виде трех составляющих по осям выбранных координат х, у, z. Направляя ось z по нормали к сечению и располагая оси х и у

в его плоскости (рис. 20, г), получаем следующие шесть составляющих:N, Q _x , Q_y , M_z ,M_x , M_y ,, где N продольная (нормальная) сила; Q_{x ,} Q_y —поперечные силы вдоль осей x и y; M_z — крутящий момент; M_x , M_y — изгибающие моменты относительно осей х к у.

Эти компоненты главного вектора и главного момента называются внутренними силовыми факторами или усилиями. Для их определения имеется шесть уравнений равновесия:

ΣХ = 0; ΣY=0; ΣZ = 0;

Σ m _x = 0; Σm_y = 0; Σ m_z = 0. (10)

Кроме проекций на соответствующую ось (или моментов относительно оси) всех внешних сил, приложенных к оставшейся части, в каждое уравнение входит только одно неизвестное усилие. Это обстоятельство подтверждает целесообразность раздельного определения составляющих главного вектора и главного момента внутренних сил, поскольку отпадает необходимость в совместном решении нескольких уравнений.

Независимо от закона распределения по сечению внутренние силы всегда приводятся к стандартной системе усилий N, Q _x , .., My, алгебраические значения которых зависят только от абсциссы сечения z. Усилия связаны с конкретными видами деформации бруса, которые подробно рассматриваются в последующих главах. Если в поперечных сечениях возникает, например, только продольная сила N, а остальные усилия отсутствуют, то брус испытывает растяжение или сжатие (в зависимости от направления силы).

При наличии только поперечной силы ( или Q_x , или Q_y , или обеих вместе) возникает сдвиг. Если не равен нулю только момент M_z , то брус работает на кручение.

При возникновении только изгибающего момента M _x или M_y брус испытывает чистый изгиб соответственно в плоскости zQ_y или zQ_x . В более общем случае к изгибающему моменту добавляется поперечная сила ( в первом случае Q_y , во втором – Q_x ).

Такой изгиб называется поперечным.

Из изложенного следует, что разложение главного вектора и главного момента внутренних сил на составляющие имеет не формальный, а чётко выраженный физический смысл.

1.6.Крутящий момент

Кручению подвергаются многие детали машин и сооружений: валы двигателей, станков и машин, оси локомотивов и моторных вагонов, элементы пространственных конструкций. Ограничимся рассмотрением вопросов, представляющих интерес с точки зрения расчёта строительных машин, а также подъёмно-транспортного и такелажного оборудования для монтажа строительных конструкций.

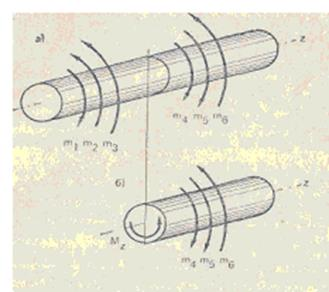
Брус испытывает кручение, если к нему прикладываются пары сил, лежащие в плоскостях, перпендикулярных его продольной оси. Моменты этих внешних пар обозначают m (рис.21, а).

Под действием внешних моментов в поперечных сечениях закручиваемого бруса возникает единственная составляющая главного момента, которая называется, как отмечалось в п.1.5, крутящим моментом и обозначается M _{z .} . Остальные составляющие главного момента, а также все составляющие главного вектора равны нулю.

Крутящий момент определяют методом сечений. Брус рассекают воображаемой плоскостью, перпендикулярной его продольной оси, мысленно отбрасывают одну из образовавшихся частей, а ее действие на оставшуюся часть заменяют неизвестным моментом M _z (рис.21, б).

После этого составляют единственное уравнение равновесия оставшейся части Σm_z =0, из которого и определяют значение М_z . Таким образом, крутящий момент в поперечном сечении бруса численно равен алгебраической сумме внешних моментов, приложенных одной стороны от рассматриваемого сечения.

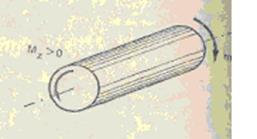
Правило знаков. Условимся считать крутящий момент положительным, если внешний момент m направлен по ходу часовой стрелки при взгляде от сечения к любому концу бруса (рис.22).

Рис.21

Рис.22

Вопрос о нахождении опасных сечений бруса, нагруженного несколькими внешними моментами, решается так же, как при растяжении (сжатии), т.е. в результате построения эпюры усилий, которое в данном случае представляет собой график изменения крутящего момента по длине бруса.

2. Строительные материалы

2.1.Бетон

Очень широкое распространение в практике строительства промышленных и жилых зданий, мостов, эстакад, водонапорных башен, опор линий электропередач и многих других сооружений получил бетон и особенно железобетон.

Существует мнение, что бетон — это сравнительно молодой материал, который начал применяться всего лет сто — двести тому назад. Однако это мнение ошибочное. Бетон — один из древнейших строительных материалов. Нам известна бетонная пирамида Нимуса, построенная более 5500 лет назад в древнем Египте. В Мексике сохранились остатки бетонных сооружений, с момента постройки которых прошло несколько тысяч лет. Великая Китайская стена, возведенная в III в. до н. э., частично тоже была бетонной. Применение бетона в древнем государстве Урарту, расположенном, как известно, на территории нашей Родины, относится к VIII в. до н. э. Но бетон, который применяется сейчас как основной строительный материал, отличается от прежнего.

Современный бетон представляет собой монолитное тело, состоящее из наполнителей в виде песка и щебня, склеенных цементом. Древние строители не знали цемента и склеивали песок и щебень глиной, гипсом или известью. Прочность такого бетона, особенно известкового, была вполне достаточной для древних построек. Некоторые древние сооружения из бетона поражают нас своими размерами и совершенством. Так, действительно кажется удивительным, что знаменитый римский Пантеон был перекрыт бетонным куполом диаметром более сорока метров. Но подобные сооружения были большой редкостью. Дело в том, что и глина, и гипс, и известь постепенно теряют свои склеивающие свойства при реакциях с водой, поэтому бетон древних расползался под воздействием дождей и туманов.

Строители древней Руси вводили в известь, идущую на изготовление бетона, толченый кирпич или бой обожженной глиняной посуды. Такие добавки (их называли цемянкой) хотя и увеличивали водостойкость бетона, на прочность и стойкость оказывали недостаточное влияние. В начале прошлого века наш соотечественник Е. Челиев впервые изготовил цемент, ставший основным клеящим веществом в процессе производства бетона.

Изготавливают цемент из смеси известняка с глиной, чаще всего берут 70—75% известняка и 25—30% глины. Для производства цемента часто употребляют доменные шлаки, глинистые сланцы, золу горючих сланцев и др. Приготовленную и тщательно перемешанную смесь подвергают обжигу в громадных вращающихся цилиндрических печах, температура обжига достигает 1500°С. Полученные зерна спекшейся смеси размалывают, получая мелкую пыль, затем вводят туда некоторые добавки (гипс и др.), повышающие качество цемента.

В процессе обжига составляющие цемент вещества теряют воду, в том числе и находящуюся в химическом соединении с ними. Благодаря этому цемент получает способность вступать в химические реакции с водой’.

Для изготовления бетона на 1 весовую часть цемента берут 2—3 части песка и 3—5 частей щебня, добавляют в полученную смесь воды и тщательно перемешивают. Готовую бетонную массу помещают в форму, соответствующую конфигурации и размерам изделия, и оставляют затвердевать.

Рассмотрим, что же происходит внутри бетонной массы при затвердевании.

При смешивании цемента с водой между ними начинается химическая реакция. При этом вокруг каждой пылинки цемента образуется слой продуктов реакции в виде студенистой массы, называемой гелем. Гель склеивает между собой песчинки и кусочки гравия. Химическая реакция теперь идет уже как между пылинками цемента и водой, так и между образовавшимся гелем и поверхностью зерен заполнителей — песка и гравия. В результате этих реакций гель постепенно теряет воду, и входящие в состав цемента химические соединения начинают образовывать кристаллы. Бетонная масса твердеет, постепенно превращаясь в твердый камнеобразный монолит.

На рисунке 23 изображено при большом увеличении внутреннее строение бетона после его отвердевания. Поверхность каждого куска щебня 1 разъедена в результате взаимодействия с гелем, причем так, что на ней возникли микроскопические кристаллики щебня, которые переплелись кристаллами, возникшими в геле 2, а последние в свою очередь переплелись с кристалликами, образовавшимися на поверхности зерен песка 3. Промежутки между кристалликами заполнены еще не прореагировавшим гелем 4 и даже не успевшими раствориться зернами цемента 5. Но на этом не остановилось протекание химических реакций во внешне затвердевшем бетоне, хотя оно затрудняется по мере возрастания числа и размеров образующихся кристаллов. По мере затвердевания

Рис. 23. Так выглядит бетон под микроскопом при сильном увеличении.

бетона эти реакции идут все медленнее и продолжаются годами и даже десятилетия­ми, а монолит бетона становится от этого все прочнее и тверже.

От каких же особенностей внутреннего строения бетона зависит его прочность и какой из образующих его частей она определяется?

Прочность щебня, идущего на изготовление бетона, обычно выбирают такой, чтобы она была в 2—3 и более раз больше прочности готового бетона, поэтому обычно не качество щебня определяет свойства бетона. Кварцевый песок, идущий на изготовление бетона, также во много раз прочнее последнего и, конечно, не его прочность определяет свойства бетона. Наименьшей прочностью из всех составляющих бетона обладает водоцементная смесь, вернее, то кристаллическое вещество, которое образуется в результате реакции цемента с водой. Отчего же зависит прочность этого вещества.

В первую очередь она зависит от количества воды в смеси. Если воды много, то в процессе затвердевания бетона она будет испаряться и создавать пузырьки, заполненные водяным паром или воздухом в массе выросших кристаллов. Эти пузырьки будут снижать прочность бетона в целом. Значит, количество воды следует брать возможно меньшим.

Но чем меньше воды, тем гуще будет водоцементная смесь и тем хуже она будет проникать в промежутки между частицами щебня и песка. Кроме того, при малом количестве воды может случиться так, что в результате испарения воды запасы ее в бетоне иссякнут прежде, чем зерна цемента успеют прореагировать с ней до полного растворения.

Как же можно разрешить эти противоречия? Очевидно, нужно уменьшить размеры пылинок цемента, тогда сократится и время их растворения. С одной стороны, это обеспечит успешное протекание реакции цемента с водой за такое время, пока мало еще испарится воды. С другой стороны, увеличение количества мелких зерен цемента приведет к появлению большего числа меньших по размеру кристалликов. Выше говорилось, что чем меньше кристалл, тем большее напряжение он выдерживает. Значит, измельчение зерен цемента приведет к упрочнению бетона.

Необходимо также обеспечить проникновение водоцементной смеси по возможности во все промежутки между частицами щебня и песка. Осуществляют это путем обработки бетонной массы вибраторами, которая не только улучшает проникновение водоцементной смеси в промежутки, но и способствует уменьшению промежутков, тем самым уплотняя бетон. Уплотнившийся бетон получается более прочным.

Прочность бетона возрастает при использовании специально подобранных песка и щебня: поверхность их зерен должна быть, возможно, более шероховатой, а состав таким, чтобы реакция между ними и гелем шла, возможно, более интенсивно. В результате сцепление между песчинками и частицами щебня возрастает, и бетон получается более прочным. Современные бетоны имеют прочность на сжатие 600—700 — и более. Но бетон очень плохо противостоит растяжению. О том, как строители борются с этим его недостатком, будет рассказано дальше.

2.2.Синтетические материалы

К числу основных синтетических материалов по важности свойств и масштабам их получения относят синтетический каучук, пластические массы и искусственные волокна.

Непрерывный и очень быстрый рост производства этих материалов во всем мире позволяет предположить, что уже в ближайшие десятилетия их выпуск должен достичь масштабов выплавки металлов.

Синтетические материалы — это высокомолекулярные органические соединения. Каждая молекула таких веществ содержит громадное количество атомов углерода и водорода, причем сочетание их бывает самым разнообразным. Молекулярный вес таких молекул-гигантов может достигать сотен тысяч, а иногда миллионов кислородных единиц.

Существенным свойством таких соединений является возможность даже при одинаковом составе входящих в молекулу атомов создавать различную структуру молекул. Вещества, имеющие одинаковый состав и молекулярный вес, но различную структуру молекул, называют изомерами. Высокомолекулярные синтетические вещества можно получать различными способами.

Можно химическими реакциями соединить в единое целое несколько (иногда очень большое количество) молекул одного и того же вещества. Такой процесс называют полимеризацией, а полученные вещества — полимерами.

Полученное вещество по своим качествам будет резко отличаться от исходного, хотя никаких посторонних примесей в него при этом и не вводится. Из одних и тех же исходных продуктов, объединяя их в молекулы различной структуры, можно получать полимеры самых разнообразных свойств.

Высокомолекулярное синтетическое вещество может быть создано путем взаимодействия нескольких химических соединений. Такой процесс называют поликонденсацией.

Широкое распространение в настоящее время получил капрон, исходным сырьем для которого служит каменный уголь. Полученные из угля фенол и карболовая кислота образуют соединение, называемое капролактамом.

Молекулы капролактама полимеризуют в молекулы-гиганты под действием высокой температуры и давления. Нагретый капролактам пропускают через маленькие отверстия и охлаждают в струе воздуха. Полученные капроновые нити имеют еще недостаточную прочность. Дело в том, что нитевидные молекулы капрона еще не рас­прямлены и расположены не вдоль оси полученной нити. Эту нить растягивают в 5 — 6 раз на специальных машинах. При этом молекулы капрона выпрямляются и располагаются вдоль оси нити. Прочность нити заметно возрастает. Аналогичным образом из угля, воды и азота воздуха получают другой синтетический материал — нейлон.

Прочность капроновых, и нейлоновых нитей на, растяжение равна прочности хорошей конструкционной стали. Кроме того, эти материалы обладают гораздо большей эластичностью, чем сталь, и неподдаются ржавлению. Но эти вещества боятся воздействия солнечного света и повышенных температур.

Не менее широкое распространение получило также другое высокомолекулярное соединение — синтетический каучук. Промышленный способ получения синтетического каучука был впервые осуществлен в нашей стране. Интересно отметить, что заводы синтетического каучука появились в Германии на 5 — 6 лет, а в США — даже на10 лет позже, чем в СССР. Способ получения синтетического каучука был разработан ленинградским профессором С. В. Лебедевым. Исходным сырьем для получения этого полимера являются древесные опилки. Из них получают этиловый спирт, который в присутствии катализаторов при температуре около 450°С разлагают, получая дивинил (бутадиен).

При высоких температурах и давлении бутадиен полимеризуют в синтетический каучук. Сырьем для получения спирта могут служить также отходы бумажных фабрик, получаемые на нефтеперегонных заводах или природные газы и др. Молекулы синтетического каучука построены в виде цепочек, и поэтому он обладает очень большой эластичностью. Добавляя в каучук различные примеси, получают резину самых разнообразных сортов и свойств.

В, наш обиход прочно вошли пластические массы самых разнообразных назначений и свойств. Из фенола и формалина вырабатывают бакелит, карболит и другие фенолоформальдегидные смолы, служащие основной составной частью пластических масс. Сочетая эти смолы с различными наполнителями, можно получить пластические массы большой прочности.

Так, растворенной в спирте искусственной смолой пропитывают ткань и сушат ее. Затем ткань складывают в стопку и спрессовывают при давлении до 200кГ/см ² . После полученный материал, широко известный под названием текстолита, обладает прочностью чугуна, но почти в 5 раз легче его. Из текстолита делают вкладыши подшипников, бесшумные шестерни и др.

Заменяя ткань бумагой, получают стеклопластик — прочный изоляционный материал.

Пропитывая фенолоформальдегидными смолами ткань, состоящую из тончайших стеклянных волокон, получают так называемый стеклопластик — очень прочный и легкий материал. Из него начинают изготавливать корпуса лодок и кузовы автомобилей. Даже фюзеляжи самолетов начинают делать из стеклопластика. Интересно отметить, что такой фюзеляж оказывается на 50% прочнее металлического.

Синтетические материалы обладают не только высокой прочностью, но и другими важными для практики свойствами. Одни не боятся кислот, другие очень плохо проводят тепло, третьи являются прекрасными изоляторами, четвертые помогают повышать урожайность на бесструктурных почвах и т. д. Все или даже основные свойства современных пластических масс рассмотреть здесь просто невозможно и интересующихся этими чудесными материалами мы отсылаем к уже упомянутым книгам Цветкова, Розена и Реутова.

3.Выбор формы детали

Существует древняя легенда о том, как жители одного города решили прославить свой город и построить для этого в нем очень высокую башню (по их понятиям — «высотой до неба»).

Много сил потратили они на постройку башни. Она постепенно росла и росла. В конце концов вес башни оказался больше той силы, которую могло бы выдержать основание башни и, по образному, но точному выражению легенды, «она сама себя раздавила».

Наиболее простые случаи расчета прочности при деформациях растяжения и сжатия очень скоро получили .свое решение, и люди поняли, что максимально допустимая высота стены, например кирпичной, не зависит от толщины. В самом де­ле, пусть известно, что стену толщиной в один кирпич можно построить высотой лишь до 50 м. Можно ли увеличить высоту стены, если строить ее толщиной в два кирпича? Очевидно, нет, так как при увеличении толщины стены в два раза также в два раза увеличится ее вес, а следовательно, сила, приходящая­ся на единицу площади основания стены, при этом не изменится.

Как же все-таки сделать стену выше? Этого можно добиться, либо увеличивая ширину основания стены без увеличения ее веса, либо уменьшая вес стены без уменьшения ширины ее основания. Для этого толщина верхней части стены должна быть меньше, чем ширина ее основания. Расчеты показывают, что при этом сечение стены должно быть ограничено кривыми линиями, форма которых зависит от прочности и удель­ного веса материала. На рисунке 24 показан характер сечения такой стены.

Казалось бы, что, изменяя так сечение, можно построить стену (или трубу) любой высоты. Но это далеко не так. По мере увеличения высоты стены ширина ее основания возрастает все быстрее и быстрее, и очень скоро даже для того, чтобы хотя бы немного увеличить высоту, потребуется очень сильно увеличивать ширину основания. Пунктиром ширину основания, и это становится невыгодным. Поэтому при строительстве была самой эко-кирпичных труб, например, используют комичной. только ту часть кривой, где основание еще возрастает медленно. При этом для простоты постройки кривые часто заменяют прямыми линиями. На рисунке 25 изображена такая труба. Пунктиром на ней показана форма расчетной кривой контура трубы. Неизменную по форме расчетную кривую линию используют в редких случаях при постройке очень высоких труб и башен.

Нетрудно понять, что по тому же самому принципу длина проволоки, подвешенной за один конец, также ограничена, так как при неограниченном удлинении прово­лока «разорвала бы сама себя». Для увеличения длины проволоки можно было бы поступить так же, как и с кирпичной трубой, только в этом случае нижний конец проволоки должен быть тоньше, чем ее верхняя часть. Так и поступают, когда, например, конструируют тросы приборов для измерения больших глубин океана и взятия проб с этих глубин.

	Рис.24. Такое наивыгоднейшее сечение должна иметь стена.
			Рис.25.Кирпичная дымовая труба. Пунктиром показано, какая форма трубы была бы самой экономичной.

Высоту стен, башен и труб можно также увеличить (как и длину свободно висящих проволок), если применить для них материалы, обладающие большей прочностью и меньшим удельным весом, чем существующие, но это — дело будущего.

При строительстве мостов и зданий требовалось не только умение строить высокие и прочные опоры и стены, но необходимо было уметь перекрыть пролеты между ними. Известные древним строителям арки и купола не всегда были удобными. Требовались другие формы перекрытий; нужно было найти такие детали, которые хорошо бы работали на изгиб.

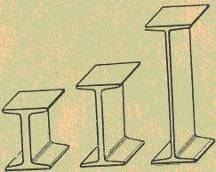
Без особого ослабления балки этот слой можно облегчить, экономя тем самым материал и делая балку тот же более легкой. Так и поступают в практике, применяя для конструкций, работающих на изгиб, балки таврового, двутаврового сечения и швеллеры .

Чем руководствуются конструкторы, устанавливая стандартные соотношения между различными размерами сечения балок?

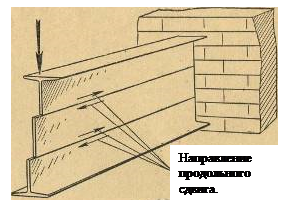
Чтобы ответить на этот вопрос, нужно рассмотреть, какие напряжения возникают в различных местах сечения изгибаемой балки (рис.26.).

Мы уже знаем, что в верхней части сечения материал балки растягивается, а нижней — сжимается, и что, кроме того, левая (в данном случае) часть балки стремится сдвинуться вниз относительно правой. Казалось бы, что для увеличения прочности балки ее конфигурацию можно менять так, как показано на рисунке 27, т. е. относя материал все дальше от нейтрального слоя и не меняя площади ее поперечного сечения. В этом слу­чае для такого же прогиба балки потребовалось бы сильнее растянуть ее верхний слой и сжать нижний, а они стали бы толще; сдвигу же сопротивлялась бы прежняя площадь балки. Но, как впервые в 1855 г. показал известный русский мостостроитель Д. И. Журавский, в результате изменения растягивающих или сжимающих балку напряжений по высоте между отдельными горизонтальными ее слоями также возникают сдвигающие усилия. Формула, носящая имя Д. И. Журавского, позволяет вычислить эти усилия в каждом конкретном случае. Понятно, что при уменьшении толщины балки в месте, прилегающем к «нейтральному слою», напряжения продольного сдвига в материале будут возрастать. Это может привести в конце концов к «расслаиванию» балки (рис. 26).

Соотношение между различными размерами сечения балки выбирают таким, чтобы балка одинаково хорошо противостояла растяжению, сжатию, поперечному и продольному сдвигу.

При увеличении длины пролета, перекрываемого балкой, начинает все сильнее сказываться возрастание ее веса. Балка «стремится переломить сама себя». Увеличение площади сечения балки не является выходом из этого затруднения, так как это привело бы к возрастанию ее веса. Следовательно, ‘при перекрытии больших пролетов балки становятся невыгодными, но ведь при строительстве мостов, ангаров, подъемных кранов необходимым требованием к конструкции является большая длина детали, работающей на изгиб.

Всем известны чудесные качества купола, созданного природой — скорлупы куриного яйца. Попробуйте раздавить его, сжимая ладонями вдоль большой оси . Если вам

и удастся это сделать, то только ценой большого усилия, а ведь отдельные кусочки яичной скорлупы ломаются чрезвычайно легко. К настоящему времени теория расчета куполов разработана очень подробно. Достаточно сказать, что имеются купола, у которых отношение толщины оболочки к диаметру в несколько раз меньше того же отношения у яичной скорлупы.

И все-таки с точки зрения современного строителя и арки и купола обладают существенными недостатками.

Главным из них является кривизна этих форм. Конечно, жителю первого этажа удобно будет иметь потолок в виде купола. Но удобно ли это будет для жителей второго этажа? Конечно, можно выровнять верхнюю сторону купола, постелив на него плоский пол.

Однако это приведет к затрате лишнего материала и сведет на нет все преимущества купола.

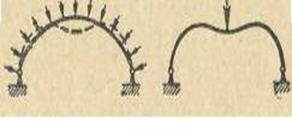
Другим существенным недостатком арок и куполов является их слабая сопротивляемость сосредоточенным на­грузкам. Рассмотрим работу арки по рисунку 28.

Слева изображена арка, на которую действует распределенная равномерно нагрузка. Вертикальная сила, действующая на верхнюю точку арки, стремится согнуть обе её половинки так, как показано пунктиром. Но другие силы, действующие на эти половинки, противодействуют такому изгибу, в результате чего материал арки работает только на сжатие.

Справа изображена арка, на которую действует только одна вертикальная сила, приложенная в верхней точке. Эта сила стремится изогнуть обе половины арки, но теперь противодействия изгибу нет, арка может разру­шиться. Сказанное выше характерно и для куполов.

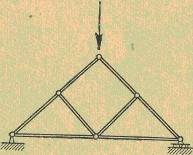
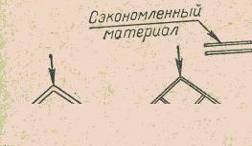
Выход из этого положения напрашивается сам: надо выпрямить обе половинки арки (рис. 29, слева), тогда вертикальная сила будет сжимать укосины полученной фермы, не изгибая их. Такое изменение фермы не только упрочняет конструкцию, но и позволяет экономить материал (укосины короче дуг арки).

Нельзя ли еще сэкономить материал, уменьшая толщину укосин, например, в два раза? Если толщину укосин просто уменьшить, то может появиться опасность возникновения продольного изгиба. Чтобы избежать этого нежелательного явления, сэкономленный на одной укосине материал надо употребить для соединения середины каждой укосины с серединой горизонтального стержня фермы. В этом случае половина материала второй укосины составит чистую экономию. Ферма теперь будет выглядеть так, как показано на рисунке 29, справа. Введение дополнительных стержней упрочняет ферму. Предположим, что действующая сила стремится вызвать продольный изгиб левой укосины, при котором ее середина — пойдет вверх. Через дополнительный стержень она потянет вверх и горизонтальный стержень фермы, но он уже растянут нижними концами укосин, следователь­но, предотвратит продольный изгиб укосины. Аналогично этому будет оказано сопротивление движению середины укосины вниз. Итак, в случае действия на ферму силы деформация изгиба фермы в целом сводится к растяжению или сжатию составляющих ее стержней. Проще всего это понять, если предположить, что стержни, образующие ферму, соединены между собой шарнирами. Введение шарниров (рис. 30) не вызовет никаких изменений в работе фермы, и прочность ее останется прежней.

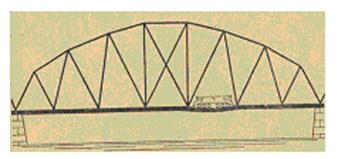
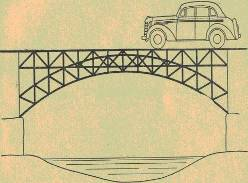
Реальные фермы должны обычно сопротивляться силам, приложенным не только в месте соединения их стержней. На рисунке 31 изображен тепловоз, идущий по мосту. Вес тепловоза вызывает изгиб только того стержня, по которому он движется в данный момент, а все остальные стержни фермы в это время работают на растяжение или сжатие. Таким образом, применение ферм позволяет свести изгиб балки по всей ее длине к изгибу только отдельного короткого стержня, а короткие балки хорошо противостоят изгибу, комбинация тонких балок-стержней в виде фермы позволяет перекрывать большие пролеты между опорами (100 м и более), чего нельзя добиться, применяя монолитные балки. При этом экономится большое количество материала.

Рис. 30. Введение шарниров не изменяет прочности фермы.

Приведенное здесь объяснение работы ферм вскрывает только важнейшие принципы, лежащие в основе их создания. Реальные фермы, конечно, являются более сложными сооружениями, чем ферма, изображенная на ри­сунке 30. Теория расчета ферм весьма сложна, и она еще не сказала своего последнего слова. Благодаря остроумным сочетаниям стержней разных сечений, длин инженеры непрерывно добиваются снижения веса сооружений и повышения их прочности, причем борьба идет за каждый процент и даже доли процента снижения затрат материала.

Огромный вклад в теорию расчета ферм внесли русские и особенно советские ученые. В середине прошлого столетия Дмитрий Иванович Журавский создал теорию расчета мостовых ферм. Особенно широкую известность в области изысканий рациональных типов прямолинейных ферм и теории арочных ферм приобрели труды выдающегося русского инженера, конструктора и изобретателя, почетного члена Академии наук СССР Владимира Григорьевича Шухова (1858 — 1939).

Он — автор прославленной русской системы перекрытий в виде висящей крыши, автор так называемых гиперболоидальных башен, состоящих из многократных одинаковых элементов. Знаменитая радиотелевизионная башня Шухова в Москве известна всему миру. Башни такого типа получили весьма ши­рокое распространение: они применяются в качестве маяков, радио- и те­левизионных башен, вышек на судах и т. д.

Часто фермы применяют в сочетании с арками (рис. 32).

Объединение фермы и арки приводит к созданию высокопрочных конструкций, позволяющих в большой степени экономить материал.

Своеобразной фермой является труба, работающая на изгиб. Прочные и легкие трубы-фермы применяются в современных конструкциях.

Иногда фермы делают из труб. Так, раму велосипеда, представляющую не что иное, как ферму, изготавливают из тонкостенных трубок, благодаря которым рама приобретает прочность и легкость.

Интересно отметить, что прежде чем люди научились строить и использовать фермы, гениальный конструктор — природа уже создала своеобразные фермы самой разнообразной конфигурации. Однако трубы хорошо сопротивляются не только деформации изгиба. Загляните под кузов автомобиля. От коробки передач к заднему мосту автомобиля идет так называемый карданный вал (рис. 33) довольно большой толщины. Для чего же его сделали таким толстым? Ответ на этот вопрос звучит парадоксально: для того, чтобы он был легче.

Карданный вал работает на скручивание (под действием собственного веса вал изгибается, но незначительно, поэтому в дальнейшем рассуждении этот изгиб мы учитывать не будем).

Деформация кручения сводится к сдвигу одних элементов материала детали по другим. При скручивании сплошного вала такой сдвиг происходит сильнее у поверхности вала, чем в его частях, лежащих около центральной оси. Именно поверхностные слои оказывают основное сопротивление скручивающим вал нагрузкам, поэтому материал середины вала целе­сообразно убрать и разместить возможно дальше от центра. Итак, валы выгоднее делать не сплошным, а трубчатыми.

Карданный вал автомобиля «Москвич» имеет диаметр около 100 мм и толщину стенок 2 мм. Если его сделать сплошным, причем равным полому валу по прочности на скручивание, то при изготовлении из того же самого материала сплошной вал должен был бы иметь диаметр 54 мм. Вес такого вала оказался бы более чем в 3,7 раза больше веса полого вала.

Казалось бы, что для получения самых прочных и легких валов их нужно выполнять в виде труб возможно большого диаметра с тонкими стенками. Однако это, как и в случае чрезмерного снижения толщины балок, может привести к продольному расслаиванию материала таких валов под действием продольных сил сдвига Д. И. Журавского.

Кроме того, в этом случае трудно будет крепить на концах таких валов шкивы, шестерни, да и возникает опасность повреждения тонких стенок вала oт случайных ударов.

Диаметр и толщину стенок полых валов в каждом частном случае выбирают исходя из конкретных условий.

Применение полых валов дает возможность делать их прочнее и в значительной степени экономить при этом материалы. Итак, мы рассмотрели только основные принципы выбора форм деталей, работающих или на сжатие, или на растяжение, или на изгиб, или на кручение. В действительности же подавляющее большинство деталей машин и сооружений вынуждено сопротивляться нагрузкам, вызывающим в них одновременно несколько деформаций разных видов. Конечно, это приводит к усложнению и выбора форм детали и ее расчета. Однако изложенные принципы являются основой такого выбора и всех расчетов на прочность.

Кроме того, мы рассматривали формы деталей, не имеющих резких переходов, канавок, выточек, сверлений, резьб и др. Как показывает практика, влияние этих факторов на прочность деталей довольно велико, и его всегда приходится учитывать.

Рис.34.Прочность детали зависит от наличия резких переходов в их формах.

.

Снижение прочности деталей при наличии резких переходов в их размерах наблюдается и в конструкциях таких сложных конфигураций, как корпус автомобиля и у таких простых деталей, как изображенный на рисунке 34 круглый вал с резким переходом одного диаметра в другой. Если диаметр толстого участка вала в 2 раза больше диаметра тонкого участка, а радиус сопряжения участка меньшего диаметра с уступом на валу в 10 раз меньше малого диаметра, то такой вал при работе на скручивание будет в 1,7 раза менее прочным, чем гладкий вал с диаметром, Прочность детали зависит от наличия резких переходов в их равным диаметру тонкого формах, конца. Если же радиус сопряжения увеличить только в 2 раза, то прочность ступенчатого вала на скручивание возрастет на 12—18% (в зависимости от материала вала и характера приложения к нему нагрузки).

Особенно велико снижение прочности деталей из-за концентрации напряжений в местах резких изменений формы в случае ударных нагрузок. Так, при испытаниях на маятниковом копре для разрушения рассмотренного ступенчатого вала понадобится вдвое менее сильный удар, чем для разрушения гладкого вала, имеющего такой же диаметр, как и тонкий конец ступенчатого вала.

Описанное явление концентрации напряжений, ведущее к снижению прочности деталей, наблюдается не только у круглых валов, но и у деталей любой формы. Поэтому конструкторы всегда стремятся сгладить эти переходы, если уж не удается вовсе избежать их при обработке деталей на станках, резцы или другие инструменты оставляют на поверхности деталей неровности, риски, задиры. Эти риски, иногда не различимые невооруженным глазом, также являются концентраторами напряжений и заметно снижают прочность деталей. Чтобы повысить эту прочность, поверхность деталей шлифуют или полируют. Несмотря на то, что при этих операциях с детали снимается часть ее материала, и сечение детали уменьшается, прочность детали заметно возрастает.

Однако умения создать высокопрочный материал и правильно выбрать форму детали из него еще недостаточно для того, чтобы обеспечить возможно большую прочность этой детали и затратить на ее изготовление как можно меньше материала. Нужно еще уметь изменять свойства материала уже готовой детали так, чтобы он как можно лучше «вел себя» в конкретных условиях ее работы.

Заключение

В результате работы над рефератом, я более подробно узнала о видах деформации, учет которых очень важен в строительстве. Познакомилась с наиболее распространенными видами строительных материалов. Узнала о том, как выбирают форму детали, для того чтобы изделие служило дольше. И получила более полное представление о том, с чем мне придется столкнуться в дальнейшей учебе.

Список литературы

[Электронный ресурс]//URL: https://inzhpro.ru/kursovaya/deformatsiya-soorujeniy/

1.Егоров А.А. Рассказ о прочности.- М.: Государственное учебно-педагогическое издательство Министерства просвещения РСФСР,1962.

2.Ицкович Г.М. Сопротивление материалов.- М.: Высшая школа,1982.

3.Касьянов В.А. Физика.10 кл.- М.: Дрофа,2003.

4.Михайлов А.М. Сопротивление материалов.- М.: Стройиздат,1989.

5.Пинский А.А. Физика.10 кл.- М.: Просвещение,1997.

6.Степин П.А. Сопротивление материалов.- М.: Высшая школа,1979.